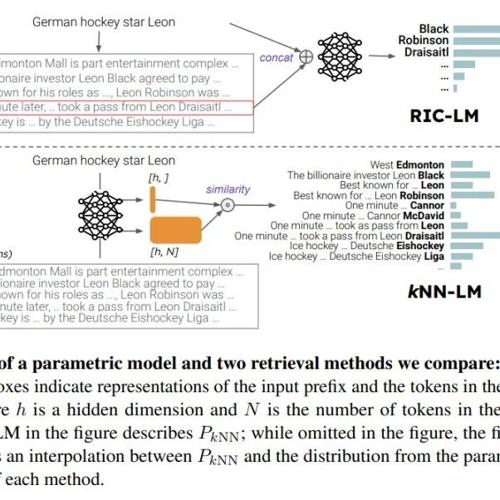
预训练大模型像“弹簧”一样,对齐微调只是暂时拉伸,任何后续微调都会让它迅速弹回预训练分布。这种“抗对齐”现象命名为 Elasticity(弹性)。
1. 研究背景:为什么对齐如此脆弱?
-
对齐方法(SFT / RLHF / DPO 等)被广泛用于让大模型“讲规矩”。 -
然而,最近不少工作发现:只需极少量(甚至非恶意)的下游微调,就能让“乖巧”的模型瞬间破功。 -
这引出一个灵魂拷问:
对齐真的改变了模型内部表征,还是仅仅在表面贴了一层“安全膜”?
2. 核心发现:语言模型的“弹性”
提出并量化了 Elasticity 概念,包含两大现象:
|
|
|
|---|---|
| Resistance(阻抗) |
|
| Rebound(回弹) |
|
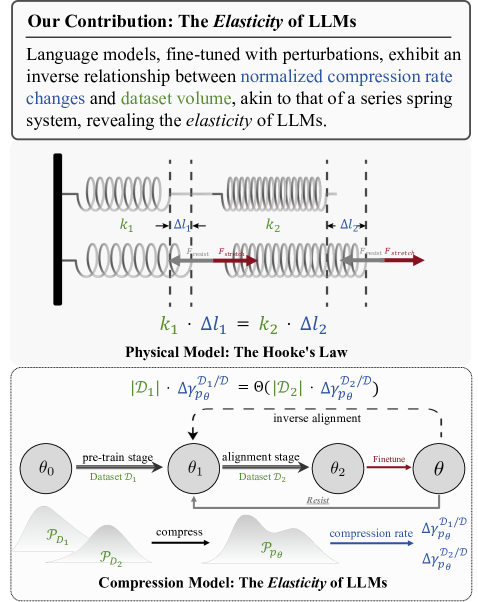
图1:语言模型的弹性。经过扰动后,归一化压缩率的变化(ΔγDi/Dpθ)和数据集的大小(|Di|)遵循反比定律,这与耦合弹簧中弹簧变形(Δli)和刚度(ki)之间的关系相似。我们推测,这种弹性导致语言模型对齐时的抗拒,从而使得逆向对齐成为可能。
3. 理论框架:用“压缩理论”刻画对齐
作者将 LLM 训练 & 对齐等价于 无损压缩 过程:
-
Token Tree:把每个可能的输出序列看成树的一条路径。 -
压缩协议:先剪枝到深度 d,再对剪枝后的子树做 Huffman 编码。 -
压缩率 与 KL 散度 一一对应,因此可用压缩率变化衡量模型行为变化。

结论:当两个数据集体积差异巨大时,微调对“小体量”数据集的影响被显著稀释,使模型天然偏向保留“大体量”预训练分布。
4. 实验验证
4.1 实验一:Resistance——“正向对齐”更难
-
设置:把 SFT 过程切成若干快照 θ₁,θ₂,…,θₙ。 -
对比两条路径 -
Path A(正向):θₖ → 在 Dₗ 上继续训练 -
Path B(逆向):θₗ → 在 Dₖ 上“反训练”
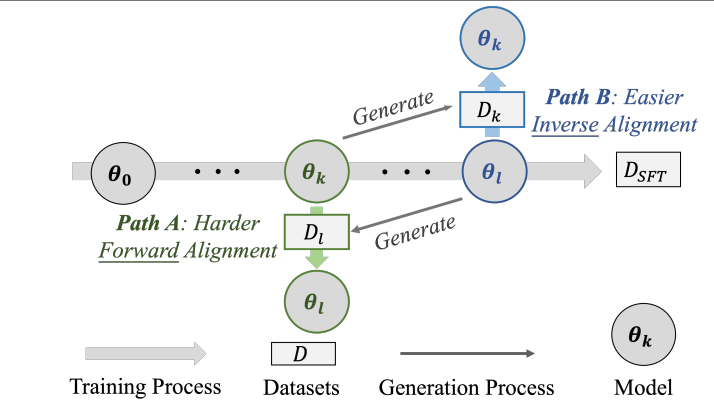
图2:Resistance 实验流程示意
-
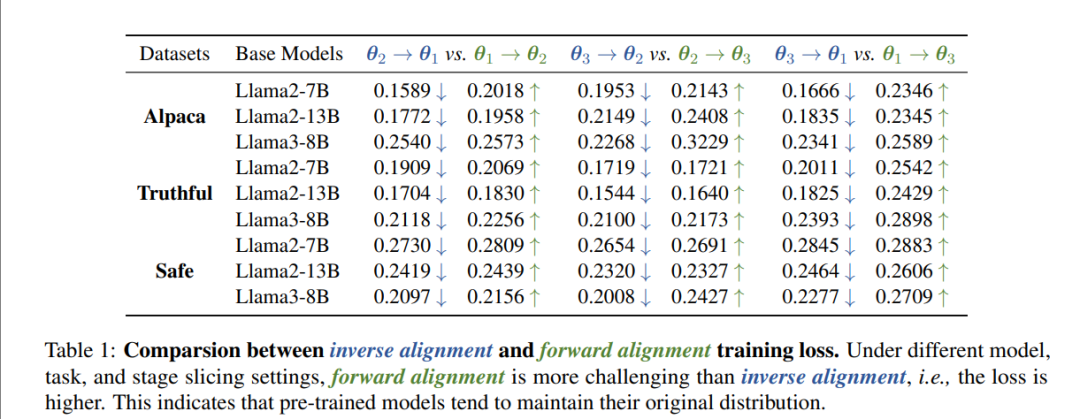
结果(表1):逆向对齐的训练损失始终更低 ⇒ 对齐确实更难!
4.2 实验二:Rebound——“回弹”速度与模型规模、预训练数据量正相关
-
任务设计: -
先用“正向”数据(安全 / 正面情感)做 SFT; -
再用“反向”数据(不安全 / 负面情感)做少量微调。
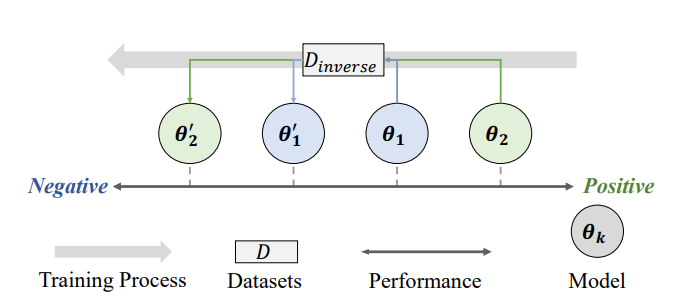
图3:Rebound 实验流程示意
-
结果:
-
正向对齐越充分,后续只需更少的负面数据即可让性能迅速崩塌。(图4) -
模型参数越大(图5)、预训练数据越多(图6),回弹越剧烈。
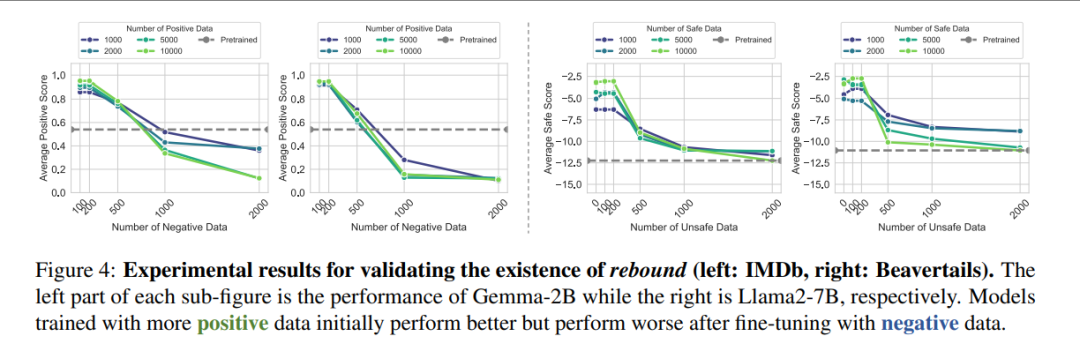
图4:回弹(Rebound)现象确凿存在
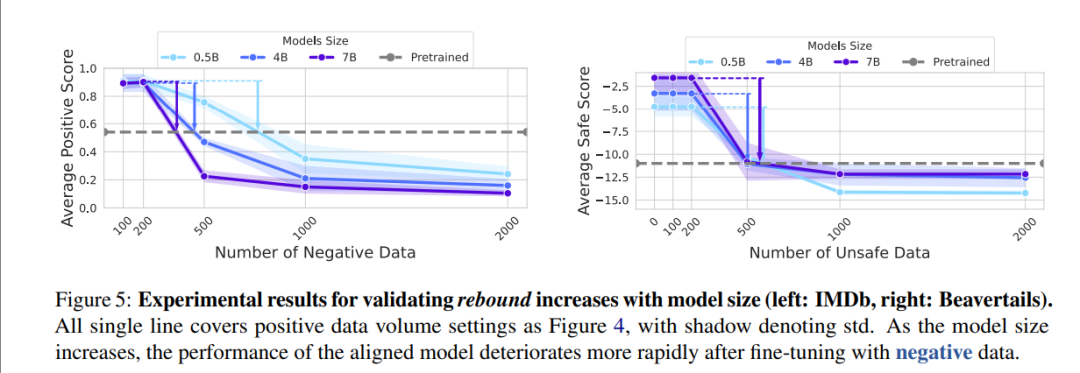
图5:模型越大,回弹越快
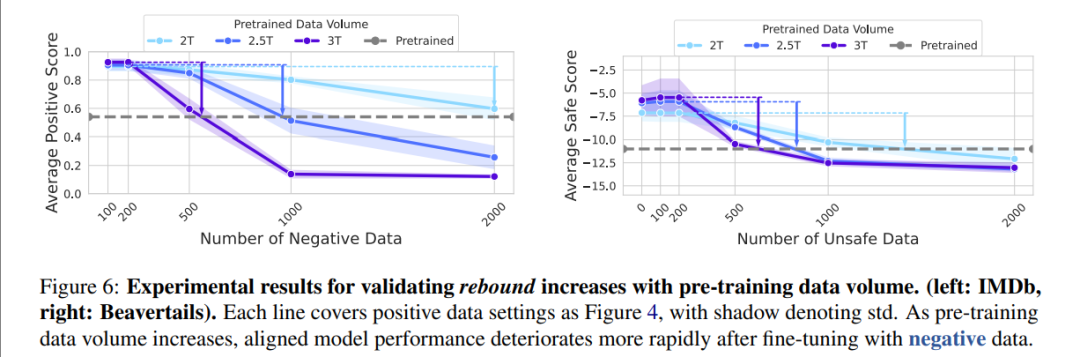
图6:预训练数据量越大,回弹越明显
https://arxiv.org/pdf/2406.06144v5https://pku-lm-resist-alignment.github.io/Language Models Resist Alignment: Evidence From Data Compression
(文:PaperAgent)