
本文提出 LeaF 框架,在知识蒸馏过程中融入基于因果分析的干扰识别机制,引导学生模型推理过程中聚焦因果关键特征,从而提升推理准确性与泛化能力。

论文标题:
Learning to Focus: Causal Attention Distillation via Gradient-Guided Token Pruning
作者单位:
中国人民大学高瓴人工智能学院,清华大学计算机系
论文链接:
https://arxiv.org/pdf/2506.07851
代码链接:
https://github.com/RUCBM/LeaF

问题背景
尽管大语言模型(LLMs)在自然语言处理任务中展现出强大的上下文理解与语言生成能力,但在长文本推理和复杂指令任务中仍存在明显不足,特别是在聚焦关键信息方面的能力较弱。这种注意力分散的现象严重制约了模型的推理准确性和生成质量。
为系统性研究这一现象,本工作首先通过教师模型与学生模型的梯度敏感性对比,识别输入中的干扰模式(distracting patterns),并在 NuminaMath-CoT 与 AceCode-87K 数据集上评估学生模型性能。
如图 1 和图 2 所示,仅仅通过剪除这些干扰信息,平均准确率即可显著提升——在数学训练集上提升超过 20%,代码训练集上提升超过 10%。
此外,在处理 AMC_AIME 等更具复杂性的任务中,模型表现出的性能提升甚至高于 GSM8K,表明复杂推理任务中往往包含更多误导性因素,干扰模型做出有效判断。
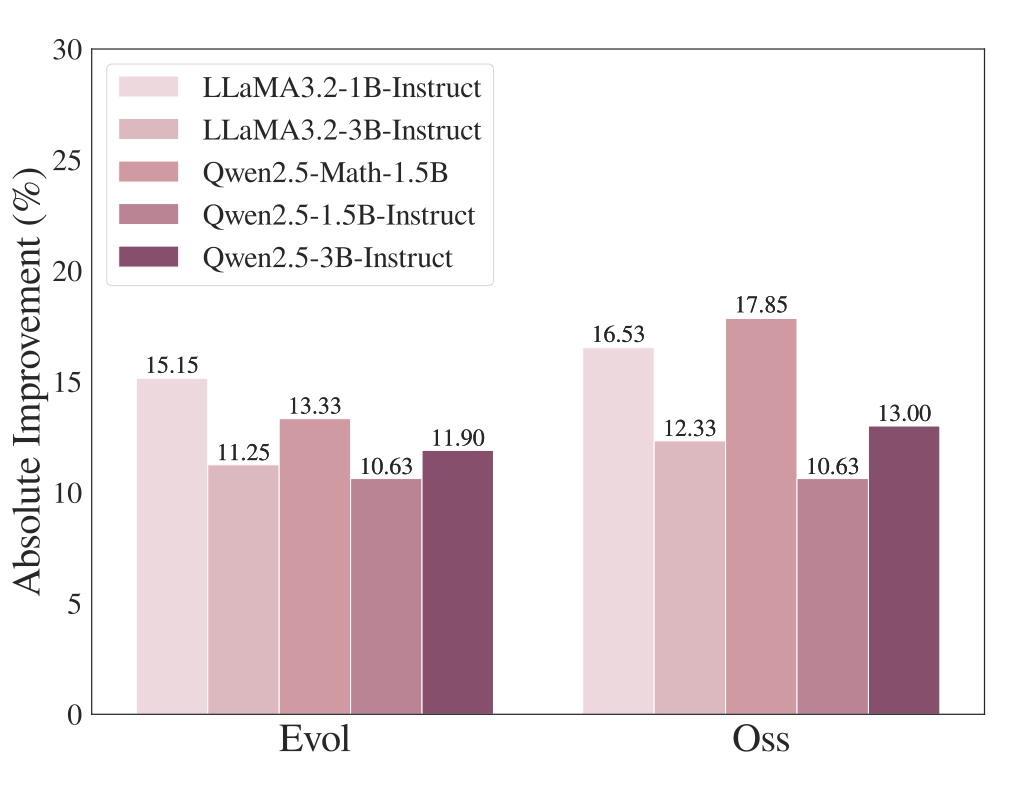
▲ 图1:代码任务准确率提升
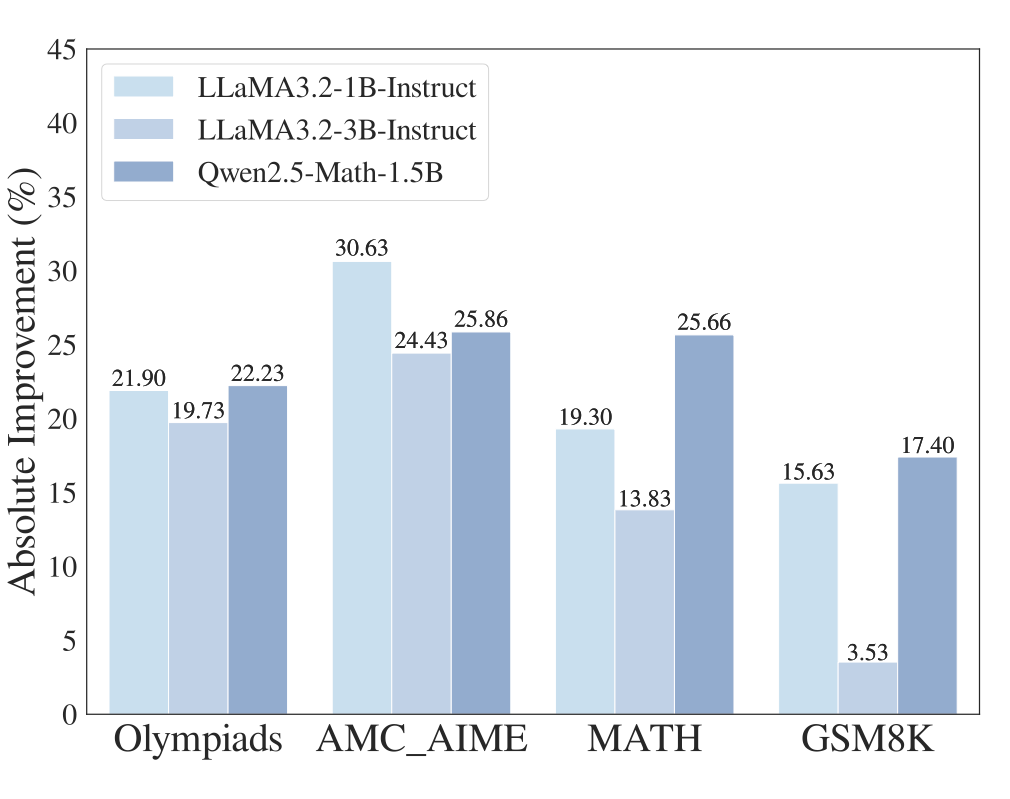
▲ 图2:数学任务准确率提升
这些发现表明,消除干扰信息、提升模型对关键信息的自主关注能力,是提升大语言模型推理性能的关键路径。
为此,作者提出 LeaF 框架,从因果视角出发,利用梯度引导识别并剔除输入中的干扰因素,引导学生模型在蒸馏过程中学习关注关键的信息区域,从而提升模型的推理表现。
实验结果表明,LeaF 在数学推理与代码生成等多个下游任务中均取得了显著性能提升。在 GSM8K、MATH 和 OlympiadBench 等数据集上,平均准确率提高了 2.41%;在 HumanEval+、LeetCode 和 LivecodeBench 等代码任务中,平均提升达到 2.48%。
此外,模型在推理过程中的注意力分布更加集中、一致性更强,注意力可视化结果也进一步验证了方法的可解释性。

LeaF:两阶段建模,提升模型注意力因果性
为缓解模型在推理过程中容易受干扰信息误导、难以聚焦关键信息的问题,作者提出了一种因果驱动的注意力迁移方法 —— LeaF(Learning to Focus) 框架。该框架由两个核心阶段构成:
干扰信息识别:用梯度刻画模型关注偏差
第一阶段旨在识别输入中对学生模型产生误导但对推理本身并非必要的 token,称为 confounding tokens。
具体地,从学生预测错误而教师预测正确的样本中,计算两者对各输入 token 的梯度敏感性对比,筛选出学生模型推理时关注(梯度值较大)而教师模型推理时不关注(梯度值较小)的 token,作为潜在干扰因素。
进一步地,若在删除这些 token 后,学生模型与教师模型都能给出正确预测,则可将其判定为 confounder tokens。即对学生推理产生误导、但对最终得出正确答案并非必要的信息。
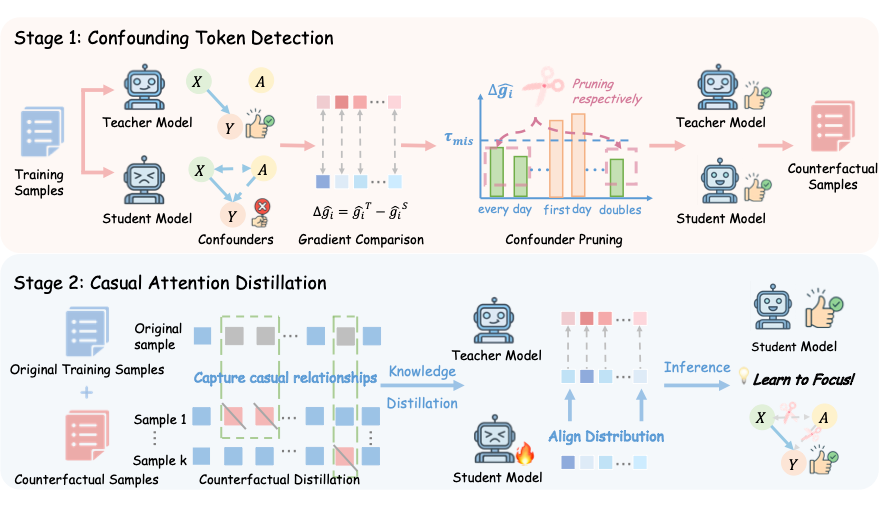
▲ 图3. LeaF 框架:通过梯度驱动的干扰识别与因果蒸馏优化推理能力
在识别 confounding tokens 后,LeaF 对比了两种构建反事实输入样本的处理方式:
-
集体移除(Collective Pruning):直接将所有识别出来的 confounding token 一次性删除;
-
连续片段移除(Span Pruning):以更精细的方式,每次仅删除一个连续干扰片段,保留更多语义上下文。
通过预实验证明,Span Pruning 更具稳定性,是更优选择。
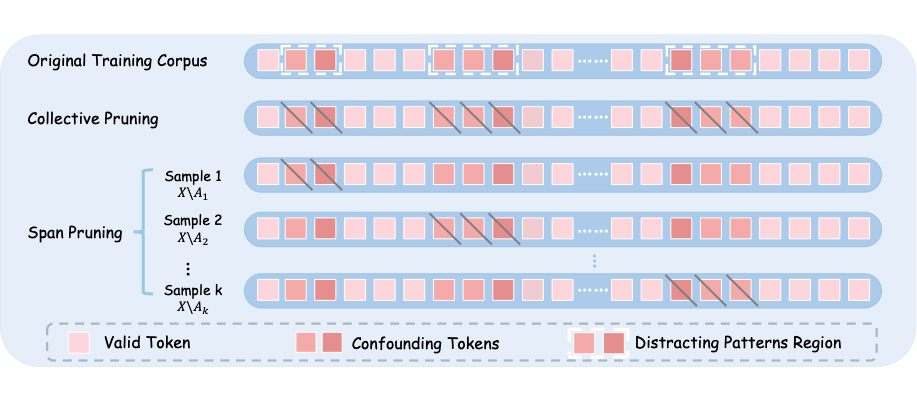
▲ 图4. 移除策略示意图
因果蒸馏:从反事实对比中学习聚焦策略
为了有效引导学生模型学习更加稳健的注意力模式,在构建好原始样本与反事实样本后,LeaF 设计了一个混合蒸馏目标,将两种监督信号融合:
-
标准蒸馏(Standard Distillation):保持学生模型在原始输入上与教师对齐;
-
反事实蒸馏(Counterfactual Distillation):鼓励学生在干扰信息被删除后的输入上依然与教师保持一致。
这种双重蒸馏机制不仅促使学生模型对齐教师模型的输出行为,更强化了其对输入中关键 token 的因果判断能力。LeaF 通过同时建模语义信息与因果依赖,有效避免学生模型仅模仿表面模式、忽略关键因果关系,从而提升推理稳健性与泛化能力。
此外,LeaF 进一步将原本仅作用于输入端的指令级处理(Instruction-level Pruning)拓展至响应级处理(Response-level Pruning)。
具体而言,除在输入指令中识别并移除干扰 token 外,LeaF 还将模型生成的历史响应视作上下文输入,动态识别其中对后续推理可能产生误导的 token 并进行删除。
该策略有助于在生成过程中持续消除干扰,进一步提升模型关注关键信息的能力,从而生成更加准确、聚焦的内容

▲ 图5 指令级处理扩展至响应级处理

实验评估:聚焦关键注意力,提升推理表现
作者在数学推理与代码生成两大任务上系统评估了 LeaF 框架的有效性,相关实验涵盖Llama和Qwen两大主流模型架构与6个评估基准,验证了LeaF在对模型推理能力的增强作用。
主实验结果
实验表明,LeaF 在所有数学与代码基准任务中均带来性能提升,平均准确率分别较标准蒸馏方法提升 2.41% 与 2.48%。其中,在高难度基准 OlympiadBench 上的改进尤为显著,表明 LeaF 能有效应对复杂推理中的注意力干扰问题。
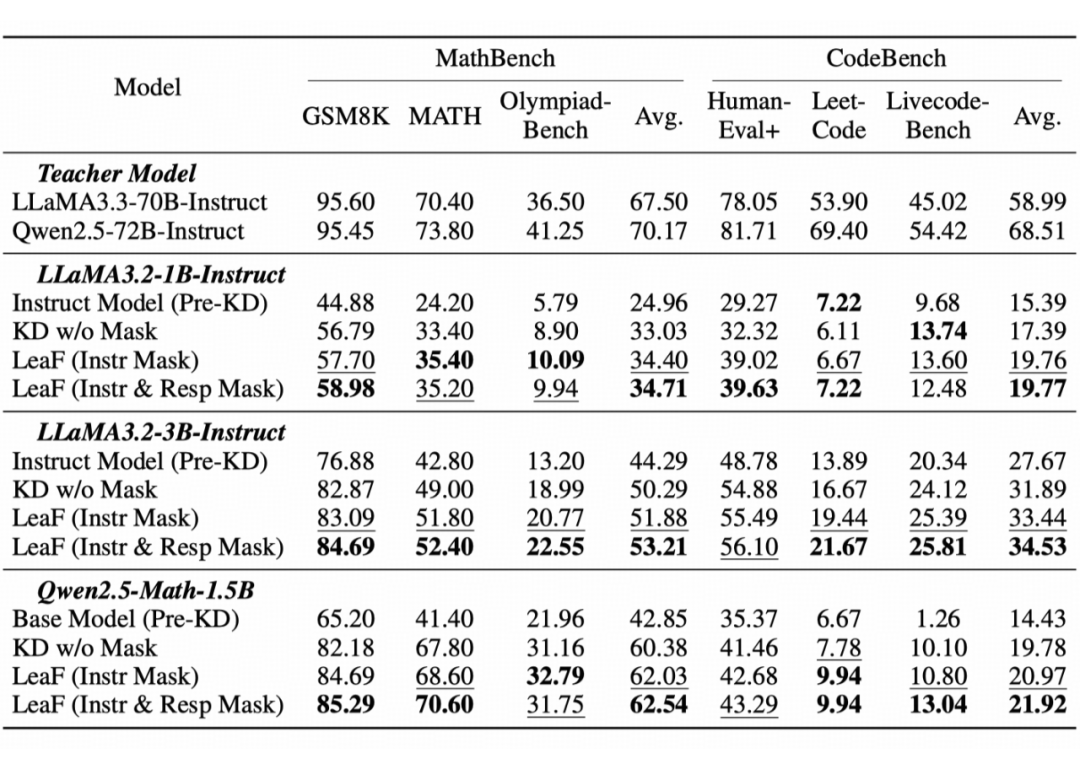
▲ 图6 主实验结果
此外,将 confounding token 的处理范围从输入指令(Instruction-level)拓展到模型生成过程(Response-level),显著提升了模型性能,表明生成阶段同样存在影响推理的干扰信息,分段处理策略有助于模型保持对关键信息的关注。

分析实验:LeaF如何精准识别并规避推理误导
为系统评估 LeaF 框架在识别并剔除干扰 token 方面的有效性,作者从四个角度展开深入分析,包括遮蔽策略、响应处理方式、阈值敏感性及案例研究,全面验证其在提升推理稳健性与模型聚焦能力方面的表现。
4.1 梯度遮蔽策略分析:LeaF如何精确识别干扰信息?
为系统评估 LeaF 所采用的梯度遮蔽策略的有效性,作者将其与两种常见遮蔽方法进行了对比实验:随机遮蔽与困惑度(PPL)遮蔽,实验在 GSM8K、MATH 和 OlympiadBench 上展开,覆盖从基础到复杂的数学任务场景。
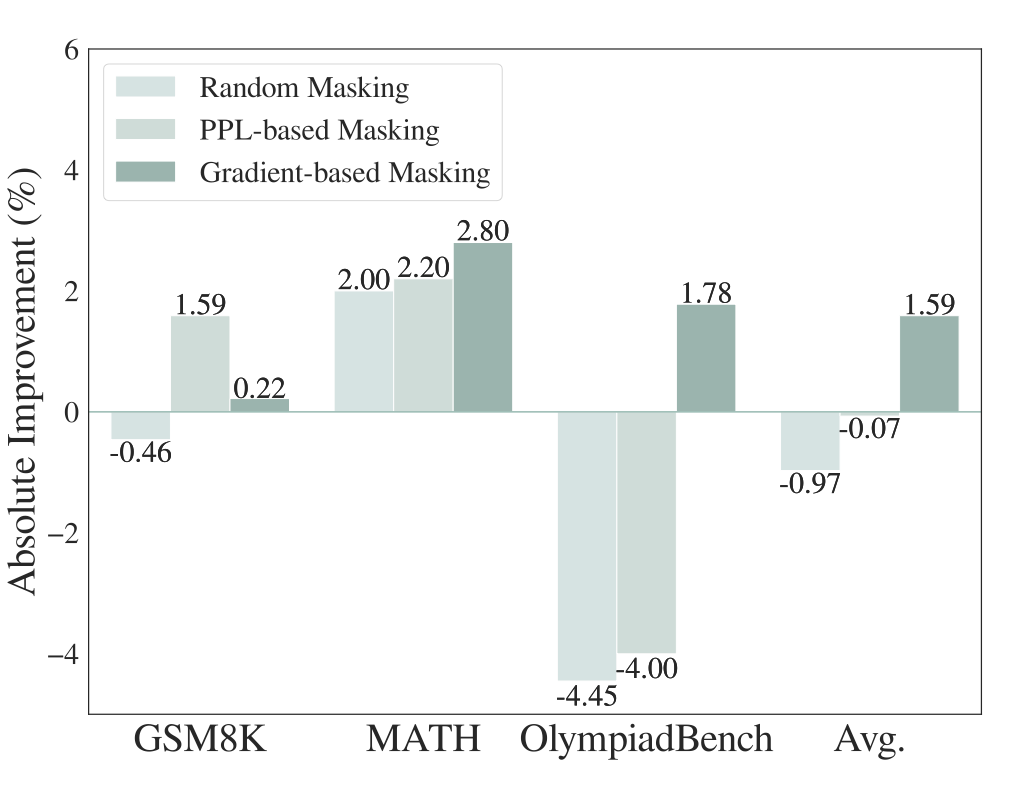
▲ 图7:LeaF 梯度遮蔽策略分析实验结果
实验观察:
-
梯度遮蔽显著优于其他策略
在 MATH 和 OlympiadBench 等复杂推理任务上取得最优表现,验证了 LeaF 的梯度引导机制能够有效定位干扰性 token。
-
随机遮蔽策略效果不稳定
在 GSM8K 和 OlympiadBench 上甚至导致性能下降,说明在缺乏语义指导的前提下,盲目删减 token 会破坏蒸馏信号,也进一步强调了仅仅通过数据增强并不足以提升模型的推理能力”。
-
困惑度遮蔽仅在简单任务中略有提升
在复杂任务(如 OlympiadBench)中效果接近随机遮蔽。这表明学生模型自身对 token 的关注可能存在偏差,难以准确判断哪些信息真正重要,凸显了引入教师模型进行对比指导的必要性。
结论:在复杂推理任务中,基于梯度差异的遮蔽策略能更精准地识别 confounder token,验证了 LeaF 框架中“教师-学生梯度对比机制”的有效性与合理性。
4.2 响应级处理策略:生成过程中的干扰信息同样不可忽视
LeaF 不仅在输入指令中识别干扰性 token(Instruct-level),还进一步将干扰检测范围扩展到模型的生成内容中(Response-level),以覆盖推理过程中的全链条注意力偏差。
为此,作者设计了三种处理策略进行对比:
-
仅处理指令级内容:只在输入文本中识别和移除干扰 token,不处理模型生成内容。
-
响应级双段处理(2段):将生成内容划分为前后两段,在每段中分别检测并去除干扰 token。
-
响应级多段处理(3段):将生成内容划分为三个连续片段,对每段独立进行干扰检测与处理。
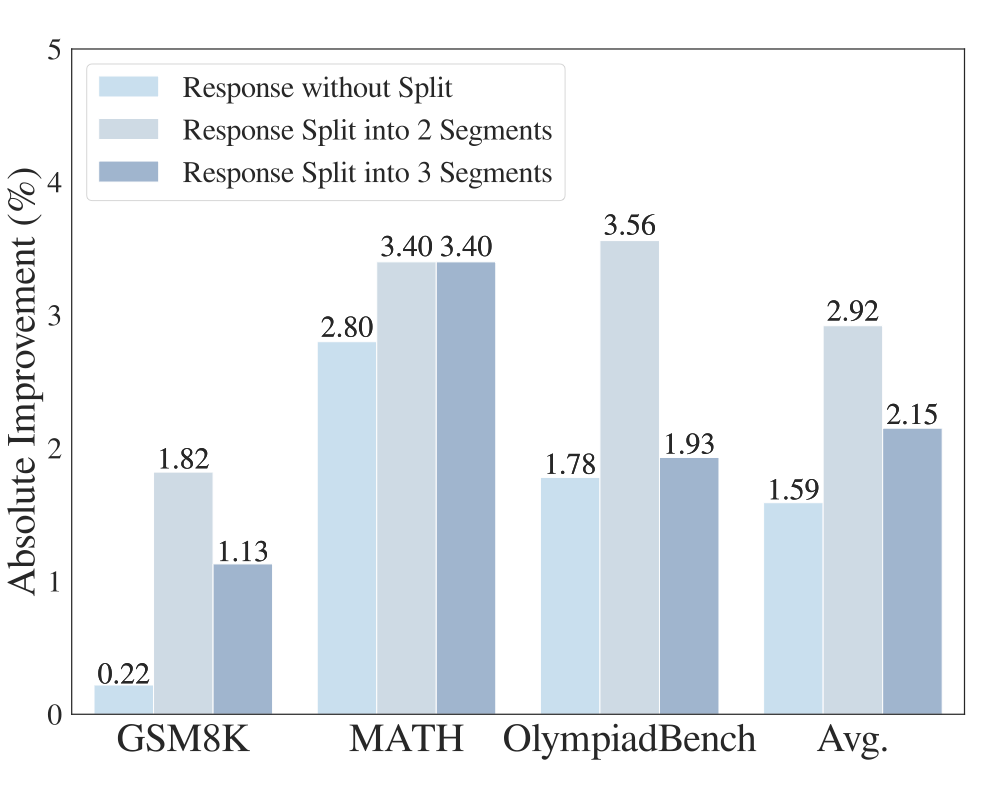
▲ 图8:LeaF 响应级处理策略实验结果
实验观察:
-
引入响应级处理显著提升模型表现:相比仅处理输入,进一步在生成过程中识别并去除干扰项,能有效增强模型的推理准确性,说明后续生成内容同样容易受到注意力偏差的干扰。
-
2 段与 3 段处理效果接近:更细粒度的三段处理未带来明显收益,说明两段已足以让模型识别并学习到 response 中的干扰模式;过度切分可能导致过拟合风险上升。
结论:Confounder tokens 不仅存在于输入指令中,也常常隐藏在模型生成路径中。将干扰识别机制扩展至生成阶段,并合理控制切分粒度,有助于提升模型在长推理任务中的注意力聚焦能力与整体表现。
4.3 阈值敏感性分析:小模型对干扰更脆弱,需更积极过滤
为了探究模型对干扰 token 的敏感程度,作者在 LeaF 框架中系统分析了用于识别 confounder tokens 的阈值(threshold)对最终推理性能的影响。
实验分别在不同模型规模(LLaMA3.2-1B 与 LLaMA3.2-3B)下,在两个层级(Instruct-level 与 Response-level)进行测试。
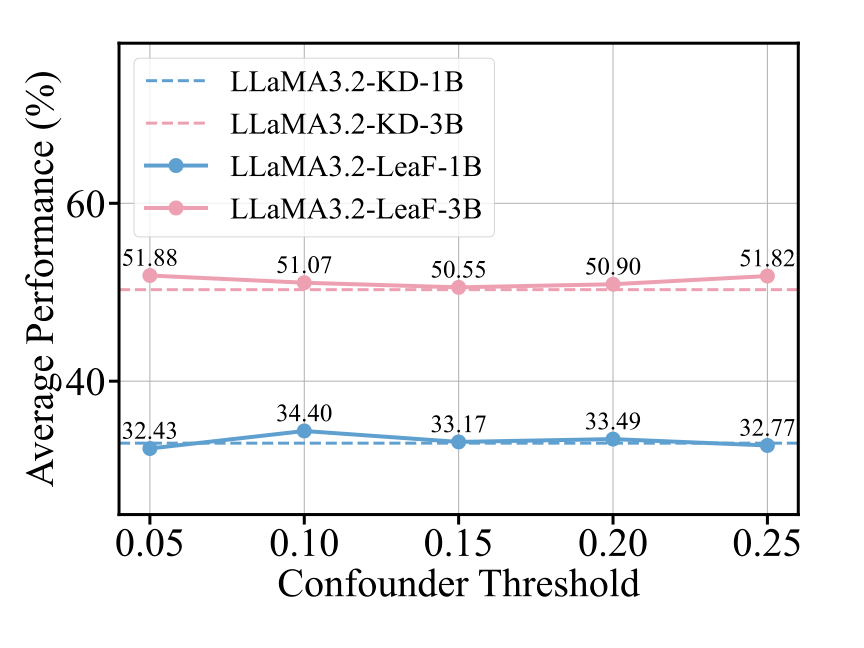
▲ 图9:Instruction-level 阈值敏感性分析(MathBench)
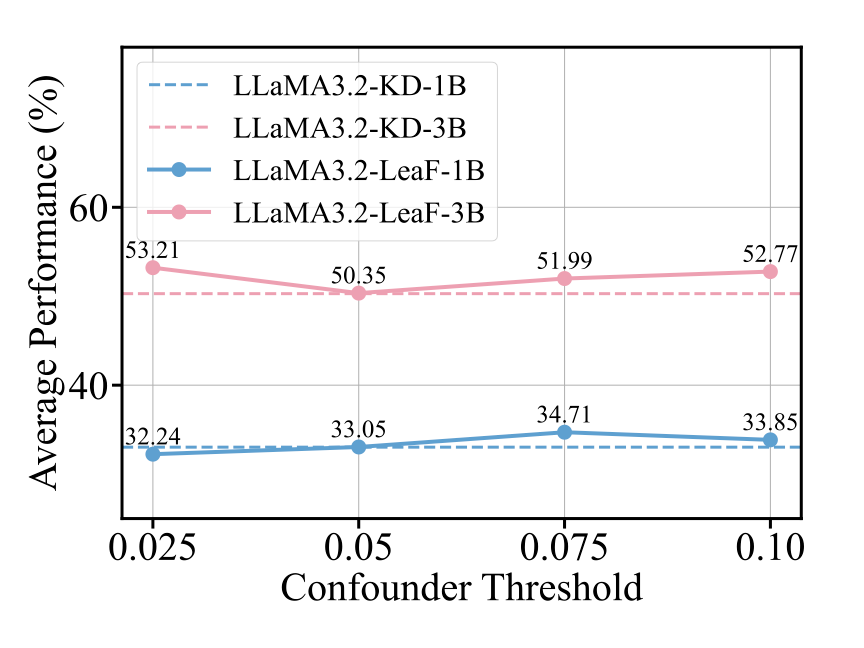
▲ 图10:Step-level 阈值敏感性分析(MathBench)
实验观察:
● Instruct-level 层级:
-
LLaMA3.2-1B 在阈值为 0.10 时表现最佳;
-
LLaMA3.2-3B 在阈值为 0.05 时达到最优性能。
● Response-level 层级:
-
LLaMA3.2-1B 在阈值为 0.15 时表现最佳;
-
LLaMA3.2-3B 则在 0.10 阈值下取得最佳效果。
分析解读:
无论是在指令层级还是生成层级,较小模型(1B)在更高阈值下效果更佳,说明其在原始输入中对干扰 token 更为敏感,因而更依赖积极的过滤策略以确保鲁棒性。
较高阈值能够更有效地识别和过滤掉这些具有误导性的 token,从而带来更好的学习效果。而大模型(3B)自身具备更强的表示与抗干扰能力,因此在更低阈值下即可获得理想表现。
结论:模型规模影响其对干扰 token 的容忍程度。较小模型更容易被误导,适合采用更高的阈值进行更积极的干扰过滤。
4.4 可解释性案例分析:模型真的学会了“聚焦关键”了吗?
为了验证 LeaF 是否真正引导模型学习到更具因果性的关注模式,作者在数学任务中构造了一个具有代表性的推理案例,比较 LeaF 与标准知识蒸馏(KD)模型在推理链条中的注意力差异。
案例任务:判断所有方程根是否为实数。
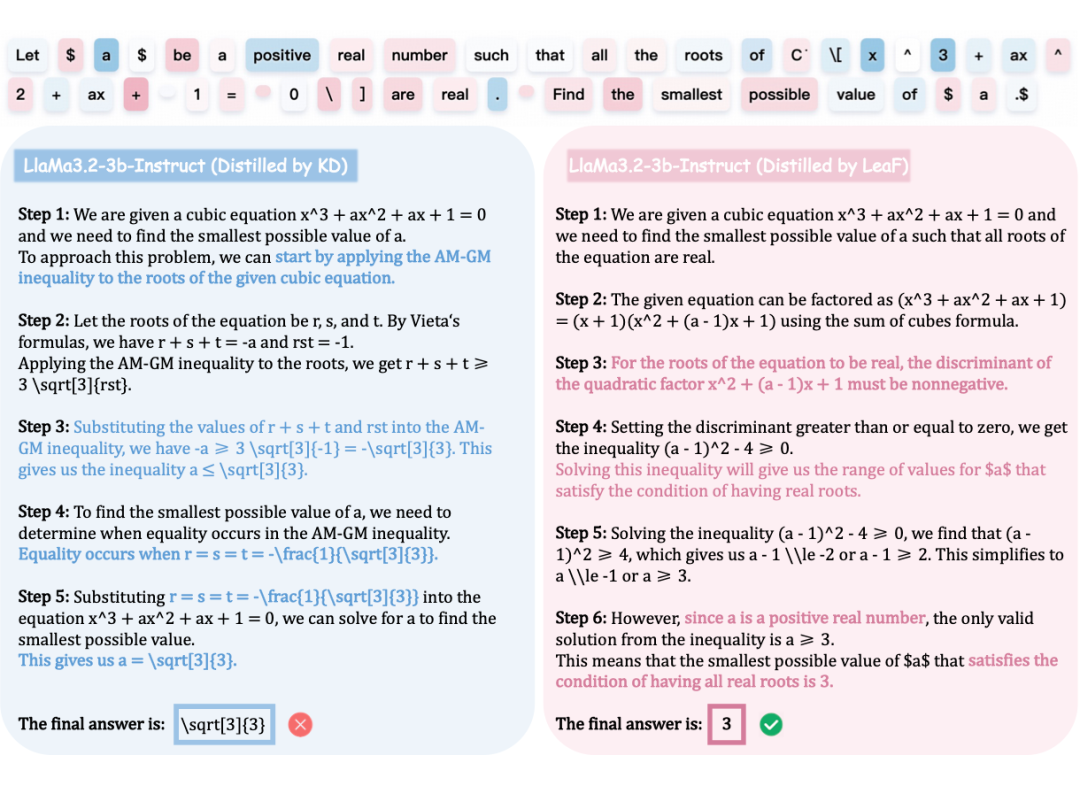
▲ 图11 案例分析
LeaF 模型的表现:
-
模型成功关注到如 “real number”、”all”、”are real” 等关键信息;
-
明确理解「所有根需为实数」这一限制,进而采取合理的推理策略:
○ 识别出 \(x = -1\) 为显然的实根;
○ 运用判别式(Discriminant)条件来确保二次因子同样产生实数解。
整个推理过程逻辑清晰、判断合理,成功得出正确答案。
KD 模型的表现:
-
忽略了“所有根需为实数”的核心条件;
-
在不考虑变量符号的情况下,错误使用 AM–GM 不等式(可能引入负数),导致最终解答错误。
分析总结:
该案例直观展示了 LeaF 帮助模型识别关键信息并构建合理推理路径的能力,从而有效规避“表层匹配式”推理误判。同时也证明 LeaF 不只是提升准确率,更能提升模型行为的可解释性与合理性。

未来展望
本工作验证了 LeaF 框架在提升大语言模型因果关注能力与推理稳健性方面的有效性,为理解和缓解注意力偏差提供了新路径。通过引入教师-学生间的梯度差异分析与反事实蒸馏机制,LeaF 能够引导模型有效识别并规避干扰性 token,从而学会聚焦真正关键的信息区域。
未来,仍有多个值得深入探索的方向。例如,当前实验主要聚焦数学与代码推理任务,进一步拓展至语言理解、问答、多跳推理等更广泛的任务场景,以验证其通用性与跨任务鲁棒性,也是未来值得研究的方向。
(文:PaperWeekly)

