
极市导读
无需做额外预训练、无需额外模型参数、无需额外数据,即插即用的正则化技术超简单实现性能提升。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
本文目录
1 Dispersive Loss:
(来自 MIT,Kaiming He 团队)
1 Dispersive Loss 论文解读
1.1 Dispersive Loss 研究背景
1.2 Dispersive Loss 介绍
1.3 Dispersive Loss 的构建过程
1.4 Dispersive Loss 的其他变体
1.5 Diffusion Model 使用 Dispersive Loss
1.6 实验设置
1.7 实验结果
太长不看版
训练扩散模型可能比你想象的更简单。
MIT 何恺明老师团队最近的工作提出:
当我们训练扩散模型的时候,可以使用表征学习的 Loss Function 辅助。
过去的十年中,Diffusion Model 的发展在很大程度上是独立于表征学习 (Representation Learning) 进行的。Diffusion Model 的训练方法很多没有参考表征学习 (主要是基于 Regression 的目标函数,缺乏显式的正则化)。
本文的 Dispersive Loss 就是一种即插即用的正则化技术,用以增强扩散模型。
Dispersive Loss 有点类似于 Contrastive 的自监督学习,鼓励内部的表征分散在隐空间中。
与 Representation Alignment (REPA) 方法相比,Dispersive Loss 方法是一种极简实现:
-
无需做额外预训练。 -
无需额外模型参数。 -
无需额外数据。
Dispersive Loss 也在多种常用模型上得到了验证,对性能有一致性地改进。
下面是对本文的详细介绍。
1 Dispersive Loss:
论文名称:Diffuse and Disperse: Image Generation with Representation Regularization
论文地址:
https://arxiv.org/pdf/2506.09027
1.1 Dispersive Loss 研究背景
扩散模型作为一种生成式模型,可以建模复杂的数据分布。另一方面,扩散模型的发展与表征学习的进展脱节了。扩散模型的训练目标通常包括一个 regression term (比如 denoising),却没有一个对表征 (用于 generation) 的 regularization term。
在表征学习 (Representation Learning) 领域,自监督学习在学习通用表征方面取得了很大进展。Contrastive Learning[1]提供了一个简单有效的框架,从样本对学习表征。这些方法鼓励 “正样本” (比较相似的样本) 之间互相吸引,”负样本” (比较不相似的样本) 之间互相排斥。使用 Contrastive Learning 的方法做 Representation Learning,已被证明在各种识别任务中很有用,包括分类、检测和分割。但是,这种学习范式对生成式建模的有效性仍是一个未被充分探索的问题。
对于这个问题,REPA[2]提出表征对齐 (Representation Alignment) 方法,利用预训练、现成的表征模型的能力做对齐。REPA 训练生成模型时,鼓励其内部表征与外部预训练模型的表征对齐。REPA 的缺点也很明显:依赖于额外的预训练、额外的模型参数以及外部数据。
虽然 REPA 在实践中产生了可观的收益,但其依赖于额外的预训练开销。更具体地说,在外部信息源上,很难讲清楚 REPA 所带来的提升是来自自监督的训练目标,还是主要来自对外部数据的计算和访问。基于以上,开发一种自给自足的极简方法,使得在做生成式建模时可以利用表征学习,仍是生成领域的一个重要的研究方向。
1.2 Dispersive Loss 介绍
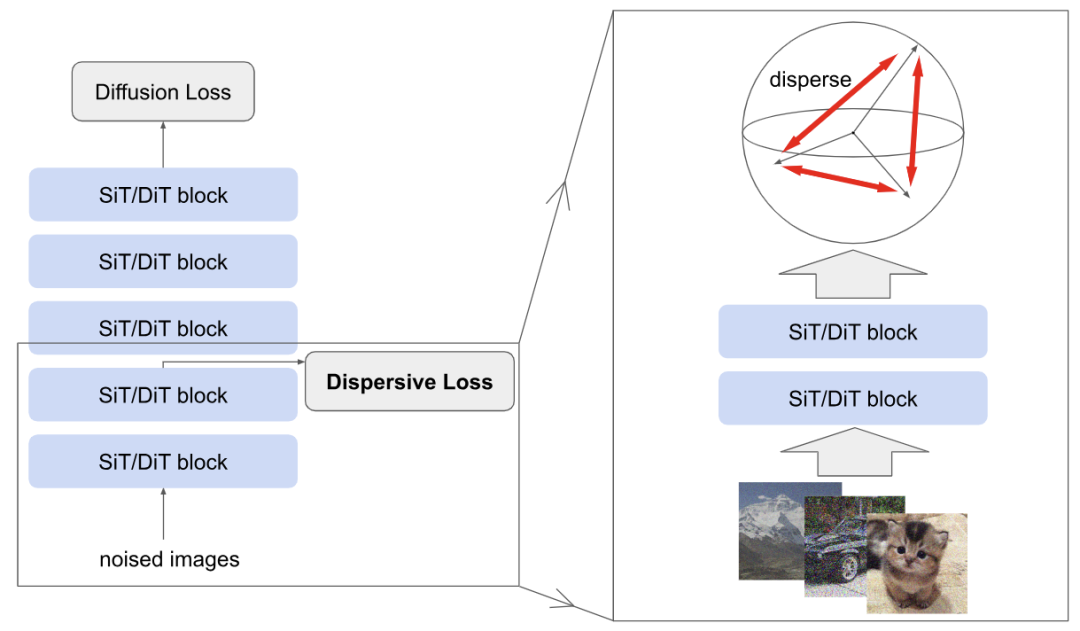
Dispersive Loss 是一种灵活,即插即用的正则化项,把自监督学习引入到了 diffusion-based 的生成式模型中。Dispersive Loss 的核心思想如图 1 所示,很简单,除了正常的回归训练目标之外,再额外地引入一个训练目标来规范模型的内部表征。
直观地讲,Dispersive Loss 会鼓励内部表征在 hidden space 中发散开,与 Contrastive Learning 中的 “排斥” 效果很像。
正式来讲,定义 为一个 batch 的噪声图片 ,这个 batch 的训练目标可以写成:

式中, 是单个 sample 的标准 Diffusion loss, 是依赖整个 Batch 的 Dispersive Loss。
在实践中,不应用任何额外的层 (例如 projection head),并且 Dispersive Loss 直接应用于中间表征,无需额外的可学习参数。
这个方法不会引入额外的采样,额外的数据增强,且权重超参数 为 0 时,1 式直接退化为 Diffusion Loss。
所引入的额外的 Dispersive Loss 只依赖此相同的 input batch 的中间表征。Dispersive Loss 与标准的 Contrastive Learning 不同,后者带来的额外的数据增强和视角可能会干扰每个 sample 的回归目标。
总而言之,Dispersive Loss 很像是 “contrastive loss without positive pairs”。与对比学习不同,它既不需要双视图采样、专门的数据增强,也不需要额外的编码器。其 Training Pipeline 可以完全遵循 Diffusion-based 或者 Flow-based 模型的方法,唯一的区别是一个额外的正则化损失,开销可以忽略不计。与 REPA 相比,Dispersive Loss 无需预训练,无需额外的模型参数,也无需外部数据。通过极简的设计,Dispersive Loss 清楚地表明,表征学习可以在不依赖外部信息源的情况下有利于生成式建模。
在生成式建模中,regression term 就已经提供了预定义的训练目标,使得无需再用 positive 的项了。这也与 Self-supervised Learning 的研究也是一致的。positive 的项被解释为对齐的目标,negative 的项被解释为正则化形式。因为现在消除了对 positive 的项的依赖,Dispersive Loss 可以被定义在任何标准 batch 数据上。
因此从概念上讲,Dispersive Loss 可以从任何现有的对比损失中,通过去除 positive 的项推导出来。从这个意义上讲,”Dispersive Loss” 并非是指特定的实现,而是指鼓励分散的一般性的训练目标。作者在下面介绍了几种变体。
1.3 Dispersive Loss 的构建过程
InfoNCE[3]是自监督学习中 contrastive loss 的一种广泛使用的变体。
令 表示输入样本 在生成模型中的中间表征,其中 表示模型计算中间层特征的那部分。原始的InfoNCE Loss 可以解释为一个分类交叉嫡目标,鼓励正对之间的相似性高,负对之间的相似性低:
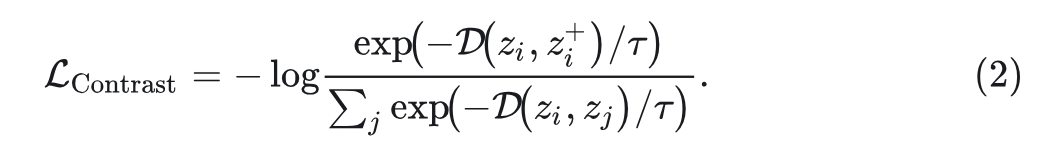
式中,表示正样本对(同一张图片做数据增强得到), 代表任何一对样本,包括正对和所有负对。 代表距离函数,常用负的余弦相似度
式 2 的分子只涉及正样本对 ,分母包括 batch 中的所有对 。上式 2 可被重写为:
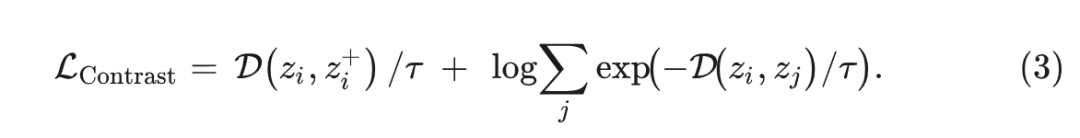
式中,第一项类似于 regression objective它最小化 与其目标 之间的距离。第二项鼓励任何一对 尽可能远。
为了构建 Dispersive Loss,只保留第二项:
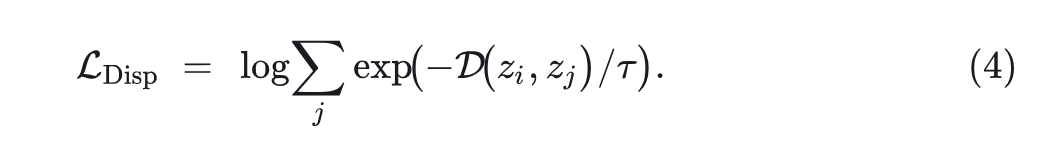
式 4 可以写成:
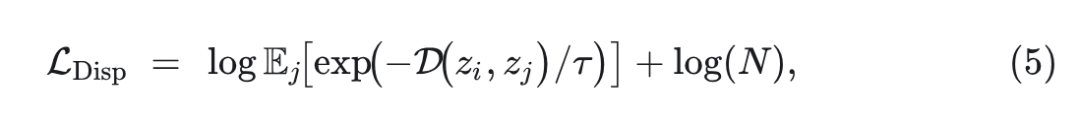
其中, 为 batch size。 是定值,可以去掉,不影响优化。
从概念上讲,这种损失定义基于参考样本 。为了有一个定义在一批样本 上的形式,式 5 可以重新定义为:
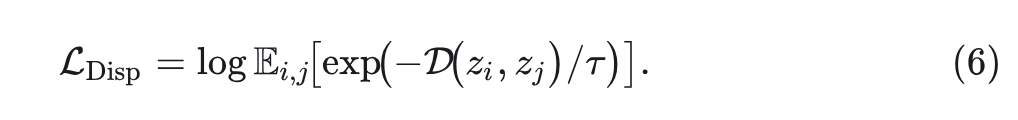
式 6 对于 batch 中的所有样本具有相同的值,每个 batch 只计算一次。在本文实验中,除了余弦相似度的距离度量之外,作者还研究了 距离: 。当使用这种 形式时,Dispersive Loss 可以很容易地用几行代码计算,如 Algorithm1 所示。

注意,在式 6 中做优化时候,我们没必要明确排除当 时的 这一项。因为在每个 batch 中不会使用同一图像的多个视图,因此该项总是定值:
形式下 。
余弦相似度情况下 。
因此,该项可以视为一个固定 bias,不影响式 6 的优化结果。因此在实践中,没有必要排除这一项,也简化了实现。
1.4 Dispersive Loss 的其他变体
Dispersive Loss 的概念自然地扩展到 InfoNCE 之外的很多 Contrastive Loss 函数。任何鼓励负样本排斥的 Training Objective 都可以被认为是 Dispersive Objective,并实例化为 Dispersive Loss 的一种。
本文引入了两种基于其他类型的对比损失函数变体。下图 2 总结了 3 个变体并比较了 contrastive 和 dispersive 的对应关系。
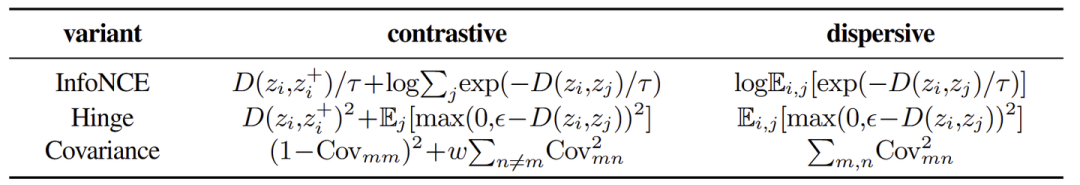
Hinge Loss
损失函数被定义为独立损失项的和,每个损失项对应一个正负对。正对的损失项为 ,负对的损失项被表述为 squared hinge loss,即 ,其中 是 margin。这里在计算 Dispersive Loss 的时候,只计算负对的项。
Covariance Loss
另一类对比损失函数对特征的协方差矩阵进行操作。Covariance Loss 希望表征的协方差矩阵与 Identity Matrix 越接近越好。作者考虑了 Barlow Twins (计算 batch 中的两个增强视图的 normalized representation 之间的交叉协方差矩阵) 定义的一种 loss 的形式。
将 交叉协方差表示为 Cov ,元素由 索引。损失鼓励对角元素 为 1 (使用损失函数 实现),鼓励非对角元素 为 0 (使用损失函数 实现)。
在 Dispersive Loss 中,只考虑非对角元素 。在这种情况下,当表征被 归一化后,对角元素 自动变为 1 ,因此 loss 函数中无需显式地定义,所以最后 Dispersive Loss 就是 。
1.5 Diffusion Model 使用 Dispersive Loss
Dispersive Loss 可以即插即用地放在生成式模型中,作为一种正则化器来使用,无需修改原有的回归损失。
Algorithm2 给出了使用 Dispersive Loss 的方法,只需要选定需要计算的中间层,并且把 Dispersive Loss 加到原来的 Diffusion Loss 即可。

1.6 实验设置
模型:DiT,SiT
VAE tokenizer 生成 32×32×4 latent space。
使用具有 250 步的基于 ODE 的 Heun Sampler 做采样。
训练 80 Epoch 的模型,并且没有 (CFG)。
默认情况下,权重 \lambda 和温度 \tau 设置为 0.5。
1.7 实验结果
Contrastive 和 Dispersive 对比
Contrastive Loss 就是把正样本对的 Loss 也算进去,创建正样本对时候使用 two view。Dispersive Loss 就不计算正样本对的。
Contrastive Loss 包含 two views,independent noise 模式代表对每个 view 独立地采样噪声;restricted noise 模式代表第 1 个视图的采样噪声,然后第 2 个视图的 noise level 限制为最多 0.005。

图 3 显示,当使用独立噪声时,所有情况下,Contrastive Loss 都未能提高生成质量。作者认为是将两个视图与完全不同的噪声水平会损害学习。因为当把 noise 做限制时,如图 3 所示,会略有提升 (3/4 的情况下)。这些实验表明,对比学习对数据增强的选择是很敏感的。虽然对比学习会有一点点帮助,但是引入额外的 view,以及 two views 直接的耦合可能限制其应用。
图 3 还显示,Dispersive Loss 相比 Baseline 就产生了一致的改进。尽管 Dispersive Loss 更加的简单,但是却比 Contrastive Loss 取得了更好的结果,即使后者使用了仔细调整的 noise。注意到 Dispersive Loss 是应用于 single view batch,它对训练的影响仅来自对中间表征的正则化效果。
Dispersive Loss 的变体
图 3 涉及到 4 种不同的 Dispersive Loss 的变体:InfoNCE ( 或者 cosine dissimilarity), Hinge, 和 Covariance。Dispersive Loss 的所有变体都优于 baseline,突出了该方法的通用性和鲁棒性。
在这些变体中, 距离的 InfoNCE 表现最好:将 FID 大幅提高 4.14,或相对 11.35%。这与自监督学习的常见做法形成对比,自监督学习通常首选余弦相似度。
作者注意到,在计算 InfoNCE Loss 之前,没有对表征应用归一化,因此,两个样本之间的距离可以任意大。作者假设这种设计可以鼓励表征更加分散,从而导致更强的正则化。默认在其他实验中使用基于 距离的 InfoNCE。
Block 的选择
图 4 研究了 Dispersive Loss 在不同层 (即 Transformer Block) 的影响。总体而言,在所研究的所有案例中,正则化器都大大优于 baseline,显示了方法的通用性。将分散损失应用于所有 Block 会产生最好的结果,同时将其应用于任何单个 Block 的性能也几乎一样好。
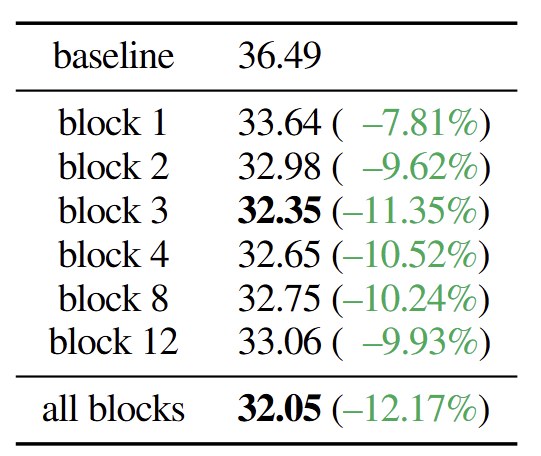
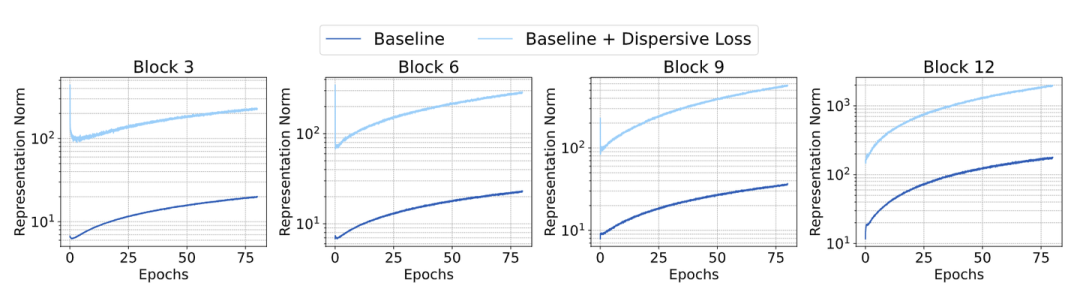
为了仔细观察,图 5 显示了模型表征的 范数,其中 Dispersive Loss 仅应用于 Block 3。值得注意的是,正则化器在 Block 3 上产生更大的表征范数,并将这种影响传播到其他所有的 Block。要知道在其他的 Block 并没有直接使用 Dispersive Loss,但是还是会被影响了。
这有助于解释图 4 中观察到的现象,即无论在哪里使用 Dispersive Loss,都会有增益。在其他实验中,作者把 Dispersive Loss 应用于第 1/4 位置的 Block。
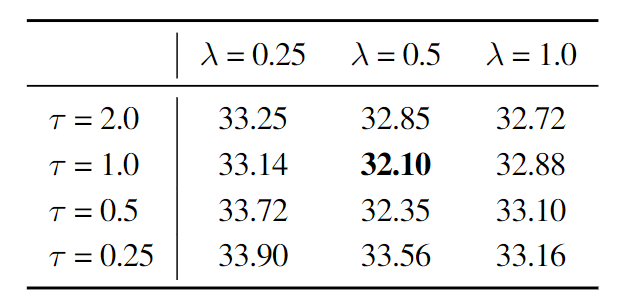
Loss 权重 和温度
Loss 权重 控制正则化的强度。作者探索了不同 Loss 权重 和温度 的影响,结果如图 6 所示。所有的配置都比 Baseline (FID 36.49) 有所改进,进一步表明正则化器有效。
不同模型使用 Dispersive Loss
到目前为止,所有的消融实验都集中在 SiT-B/2 模型上。图 7 中作者在四个常用的模型大小 (S, B, L, XL) 上把 Dispersive Loss 验证到 DiT 和 SiT。Dispersive Loss 在所有场景中始终可以提高 Baseline 性能。
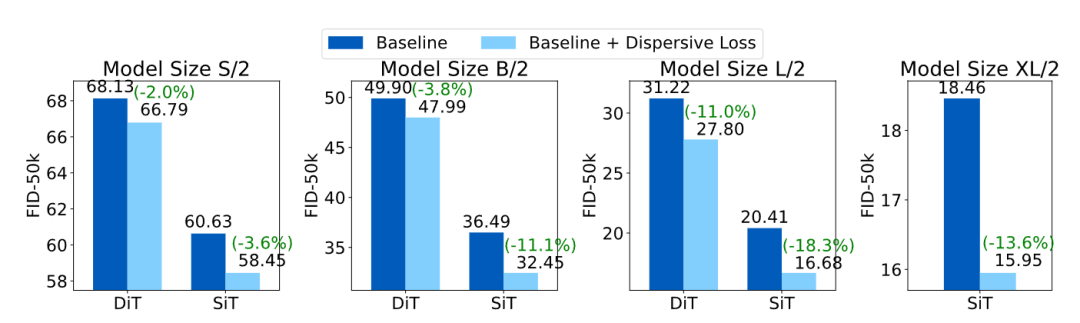
有趣的是,可以观察到当 Baseline 更强时,改进都更大。
-
对于每个特定的模型大小,SiT 相对和绝对改进都大于 DiT。SiT 比 DiT 更强。 -
与 B 或 S 大小模型相比,L 大小模型表现出更大的相对改进。
总体而言,这一趋势提供了强有力的证据,证明 Dispersive Loss 的主要作用在于正则化。更大的模型往往更趋向于过拟合,因此往往会从正则化中受益更多。
SiT-XL/2 更多实验
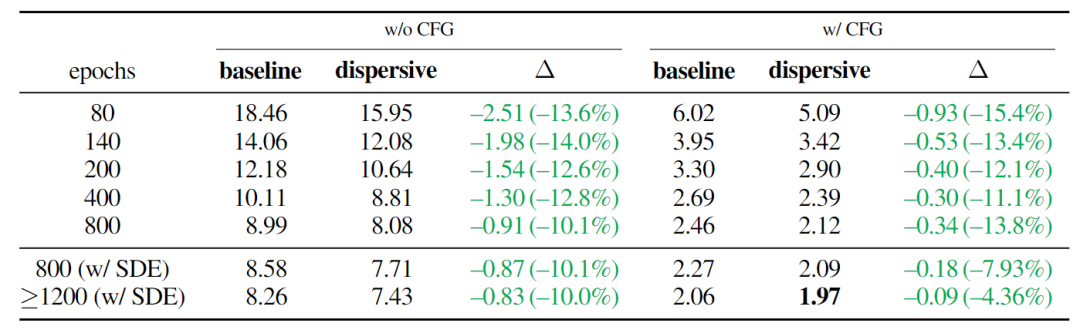
图 8 中作者训练了 SiT-XL/2。在 w/ 和 w/o CFG 的情况下训练模型更多 Epoch。研究了基于 ODE 和基于 SDE 的 Sampler。总体而言,Dispersive Loss 在所有设置中都被证明是有益的,即使在 Baseline 变得更强时。该模型生成的一些示例图像如图 9 所示。

与 REPA 的 System-level 比较
虽然本文的正则化器直接对模型的内部表示进行操作,但 REPA 将它们与来自外部模型的那些对齐。
因此,为了公平比较,应考虑额外的计算开销和外部信息源,如图 10 所示。

相比之下,本文方法是完全自给自足,无需预训练,无需外部数据,也无需额外的模型参数。当将训练扩展到更大的模型和数据集时,本文方法很适用。
一步生成模型
本文方法可以直接推广到基于一步扩散的生成模型。在图 11 (左) 中,作者将 Dispersive Loss 应用于最近的 MeanFlow 模型[4],并观察到一致的改进。图 11 (右) 将这些结果与最新的基于 One-step Diffusion-based 模型或者 Flow-based 模型进行了比较。结果表明,本文方法增强了 MeanFlow。

参考
-
Momentum contrast for unsupervised visual representation learning -
Representation alignment for generation: Training diffusion transformers is easier than you think -
Representation learning with contrastive predictive coding -
Mean flows for one-step generative modeling
(文:极市干货)

