博客来源:https://leimao.github.io/blog/Row-Major-VS-Column-Major/ ,来自Lei Mao,已获得作者转载授权。
Row-Major VS Column-Major
简介
在计算领域中,行主序(row-major order)和列主序(column-major order)是将多维数组存储在线性存储(如随机存取内存)中的两种方式。下图展示了二维矩阵的行主序和列主序存储方式。
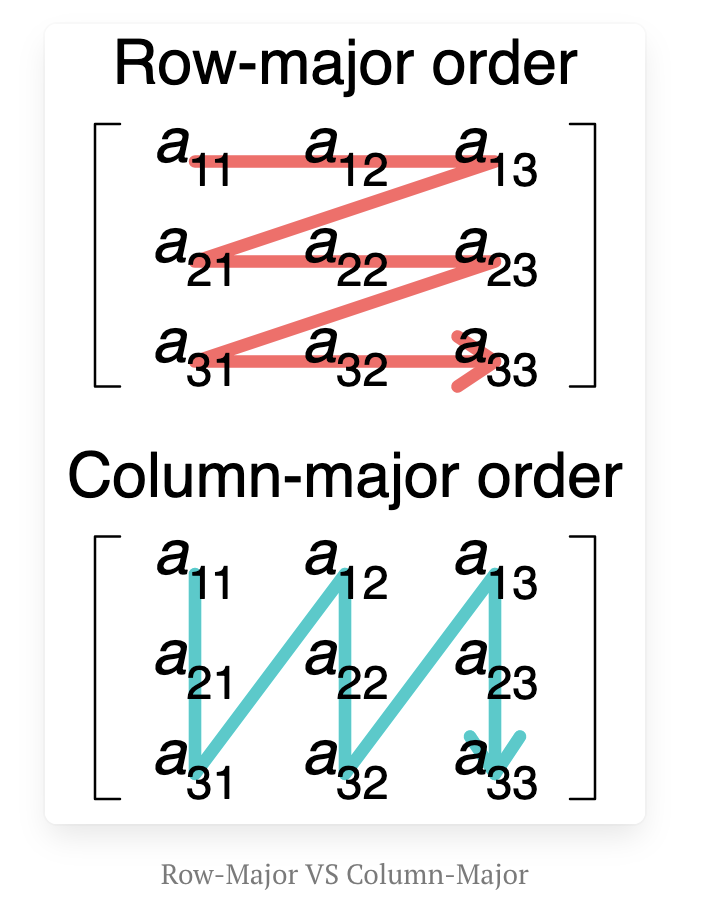
在这篇博客文章中,我将讨论行主序和列主序之间的差异,以及它们对矩阵乘法性能的影响。
Row-Major VS Column-Major
给定一个形状为 的矩阵 ,如果它以行主序(row-major order)存储,其leading dimension是 ,如果它以列主序(column-major order)存储,其leading dimension是 。
要从存储 的同一块内存中读取 ,其中 以行主序存储且leading dimension为 ,我们可以将内存中的矩阵视为以列主序存储,leading dimension仍然是 。
要从存储 的同一块内存中读取 ,其中 以列主序存储且leading dimension为 ,我们可以将内存中的矩阵视为以行主序存储,leading dimension仍然是 。
例如,我们有一个矩阵 :
如果 以行主序存储,矩阵在线性内存中的值为 。 如果 以列主序存储,矩阵在线性内存中的值为 。
的转置 为:
如果 以行主序存储,矩阵在线性内存中的值为 。 如果 以列主序存储,矩阵在线性内存中的值为 。
可以很容易看出, 以行主序存储在内存中与 以列主序存储在内存中完全相同,而 以列主序存储与 以行主序存储在内存中完全相同。
对于以行主序存储的矩阵 ,读取 的行和读取 的列是快速且缓存友好的,而读取 的列和读取 的行是缓慢的且会使缓存失效。
对于以列主序存储的矩阵 ,读取 的列和读取 的行是快速且缓存友好的,而读取 的行和读取 的列是缓慢的且会使缓存失效。
矩阵乘法
在内存中存储矩阵的方式会影响许多处理器(如CPU和GPU)上矩阵乘法的性能。通常,根据矩阵乘法是否需要对矩阵进行数学转置,有四种计算矩阵乘法的方式:、、 和 。尽管这些操作的理论MAC数相同,但根据矩阵 和 的存储顺序,每种方式的性能表现会有所不同。
假设矩阵 的形状为 ,矩阵 的形状为 ,要计算 ,其中 是形状为 的矩阵, 中的每个元素都是矩阵 中大小为 的一行与矩阵 中大小为 的一列的累积和。
根据两个矩阵的存储顺序,有四种情况:
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
当 以行主序存储, 以列主序存储时,由于现代处理器的缓存机制,从 读取行和从 读取列都很快,而更快的读取会带来更好的性能(在相同的计算量下)。
因此,矩阵乘法 更适合 以行主序存储、 以列主序存储的情况。
假设矩阵 的形状为 ,矩阵 的形状为 ,要计算 ,其中 是形状为 的矩阵, 中的每个元素都是矩阵 中大小为 的一列与矩阵 中大小为 的一列的累积和。
根据两个矩阵的存储顺序,有四种情况:
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
当 以列主序存储, 以列主序存储时,由于现代处理器的缓存机制,从 读取列和从 读取列都很快,而更快的读取会带来更好的性能(在相同的计算量下)。
因此,矩阵乘法 更适合 以列主序存储、 以列主序存储的情况。
假设矩阵 的形状为 ,矩阵 的形状为 ,要计算 ,其中 是形状为 的矩阵, 中的每个元素都是矩阵 中大小为 的一行与矩阵 中大小为 的一行的累积和。
根据两个矩阵的存储顺序,有四种情况:
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
当 以行主序存储, 以行主序存储时,由于现代处理器的缓存机制,从 读取行和从 读取行都很快,而更快的读取会带来更好的性能(在相同的计算量下)。
因此,矩阵乘法 更适合 以行主序存储、 以行主序存储的情况。
假设矩阵 的形状为 ,矩阵 的形状为 ,要计算 ,其中 是形状为 的矩阵, 中的每个元素都是矩阵 中大小为 的一列与矩阵 中大小为 的一行的累积和。
根据两个矩阵的存储顺序,有四种情况:
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
当 以列主序存储, 以行主序存储时,由于现代处理器的缓存机制,从 读取列和从 读取行都很快,而更快的读取会带来更好的性能(在相同的计算量下)。
因此,矩阵乘法 更适合 以列主序存储、 以行主序存储的情况。
矩阵乘法偏好
不同存储顺序组合下被乘矩阵的矩阵乘法偏好可以总结如下:
|
|
|
|
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
由于通常一个软件框架中的所有矩阵都会使用相同的存储顺序,这意味着在这些场景下只有 和 是首选的。
优化可以减少最优矩阵乘法选项与其他选项之间的性能差距,有时甚至可以减少到几乎为零,这取决于具体的实现和处理器。
此外,有时为了使用四种矩阵乘法选项中性能最好的一种而在内存中物理转置矩阵并不是一个好主意,因为转置矩阵的开销可能远大于四种矩阵乘法选项之间的差异,特别是当它们都经过良好优化时。
矩阵乘法基准测试
此外,我们可以使用C++单线程简单实现来验证我们的分析。
#include <cassert>
#include <chrono>
#include <cstdint>
#include <functional>
#include <iomanip>
#include <iostream>
#include <tuple>
#include <utility>
#include <vector>
template <class T>
float measure_performance(std::function<T(void)> bound_function,
int num_repeats = 100, int num_warmups = 100)
{
for (int i{0}; i < num_warmups; ++i)
{
bound_function();
}
std::chrono::steady_clock::time_point time_start{
std::chrono::steady_clock::now()};
for (int i{0}; i < num_repeats; ++i)
{
bound_function();
}
std::chrono::steady_clock::time_point time_end{
std::chrono::steady_clock::now()};
auto time_elapsed{std::chrono::duration_cast<std::chrono::milliseconds>(
time_end - time_start)
.count()};
float latency{time_elapsed / static_cast<float>(num_repeats)};
return latency;
}
// A and B are column-major matrices.
template <typename T>
void mm_a_col_major_b_col_major(T const* A, T const* B, T* C, uint32_t m,
uint32_t n, uint32_t k, uint32_t lda,
uint32_t ldb, uint32_t ldc, bool is_A_transpose,
bool is_B_transpose)
{
for (uint32_t ni{0}; ni < n; ++ni)
{
for (uint32_t mi{0}; mi < m; ++mi)
{
// Compute C[mi, ni]
T accum{0};
// A * B
if ((!is_A_transpose) && (!is_B_transpose))
{
for (uint32_t ki{0}; ki < k; ++ki)
{
// A[mi, ki] * B[ki, ni]
accum += A[ki * lda + mi] * B[ni * ldb + ki];
}
}
// A^T * B
else if ((is_A_transpose) && (!is_B_transpose))
{
for (uint32_t ki{0}; ki < k; ++ki)
{
// A[ki, mi] * B[ki, ni]
accum += A[mi * lda + ki] * B[ni * ldb + ki];
}
}
// A * B^T
else if ((!is_A_transpose) && (is_B_transpose))
{
for (uint32_t ki{0}; ki < k; ++ki)
{
// A[mi, ki] * B[ni, ki]
accum += A[ki * lda + mi] * B[ki * ldb + ni];
}
}
// A^T * B^T
else
{
for (uint32_t ki{0}; ki < k; ++ki)
{
// A[ki, mi] * B[ni, ki]
accum += A[mi * lda + ki] * B[ki * ldb + ni];
}
}
C[ni * ldc + mi] = accum;
}
}
}
void print_latency(float latency)
{
std::cout << std::fixed << std::setprecision(3) << "Latency: " << latency
<< " ms" << std::endl;
}
int main()
{
constexpr uint32_t num_repeats{10};
constexpr uint32_t num_warmups{10};
constexpr uint32_t M{256};
constexpr uint32_t K{256};
constexpr uint32_t N{256};
std::vector<float> matrix_a(M * K);
std::vector<float> matrix_b(K * N);
std::vector<float> matrix_c(M * N);
float const* A{matrix_a.data()};
float const* B{matrix_b.data()};
float* C{matrix_c.data()};
uint32_t const matrix_a_col_major_ld{M};
uint32_t const matrix_a_row_major_ld{K};
uint32_t const matrix_a_transpose_col_major_ld{matrix_a_row_major_ld};
uint32_t const matrix_a_transpose_row_major_ld{matrix_a_col_major_ld};
uint32_t const matrix_b_col_major_ld{K};
uint32_t const matrix_b_row_major_ld{N};
uint32_t const matrix_b_transpose_col_major_ld{matrix_b_row_major_ld};
uint32_t const matrix_b_transpose_row_major_ld{matrix_b_col_major_ld};
uint32_t const matrix_c_col_major_ld{M};
uint32_t const matrix_c_row_major_ld{N};
uint32_t const matrix_c_transpose_col_major_ld{matrix_c_row_major_ld};
uint32_t const matrix_c_transpose_row_major_ld{matrix_c_col_major_ld};
std::function<void(void)> const mm_a_col_major_b_col_major_a_b{
std::bind(mm_a_col_major_b_col_major<float>, A, B, C, M, N, K,
matrix_a_col_major_ld, matrix_b_col_major_ld,
matrix_c_col_major_ld, false, false)};
std::function<void(void)> const mm_a_col_major_b_col_major_a_transpose_b{
std::bind(mm_a_col_major_b_col_major<float>, A, B, C, M, N, K,
matrix_a_transpose_col_major_ld, matrix_b_col_major_ld,
matrix_c_col_major_ld, true, false)};
std::function<void(void)> const
mm_a_col_major_b_col_major_a_transpose_b_transpose{std::bind(
mm_a_col_major_b_col_major<float>, A, B, C, M, N, K,
matrix_a_transpose_col_major_ld, matrix_b_transpose_col_major_ld,
matrix_c_col_major_ld, true, true)};
std::function<void(void)> const mm_a_col_major_b_col_major_a_b_transpose{
std::bind(mm_a_col_major_b_col_major<float>, A, B, C, M, N, K,
matrix_a_col_major_ld, matrix_b_transpose_col_major_ld,
matrix_c_col_major_ld, false, true)};
std::cout << "C = A * B" << std::endl;
float const latency_a_b = measure_performance(
mm_a_col_major_b_col_major_a_b, num_repeats, num_warmups);
print_latency(latency_a_b);
std::cout << "C = A^T * B" << std::endl;
float const latency_a_transpose_b = measure_performance(
mm_a_col_major_b_col_major_a_transpose_b, num_repeats, num_warmups);
print_latency(latency_a_transpose_b);
std::cout << "C = A * B^T" << std::endl;
float const latency_a_b_transpose = measure_performance(
mm_a_col_major_b_col_major_a_b_transpose, num_repeats, num_warmups);
print_latency(latency_a_b_transpose);
std::cout << "C = A^T * B^T" << std::endl;
float const latency_a_transpose_b_transpose =
measure_performance(mm_a_col_major_b_col_major_a_transpose_b_transpose,
num_repeats, num_warmups);
print_latency(latency_a_transpose_b_transpose);
assert(latency_a_transpose_b ==
std::min({latency_a_b, latency_a_transpose_b, latency_a_b_transpose,
latency_a_transpose_b_transpose}));
assert(latency_a_b_transpose ==
std::max({latency_a_b, latency_a_transpose_b, latency_a_b_transpose,
latency_a_transpose_b_transpose}));
}
我们可以看到,给定矩阵 和矩阵 都以列主序存储,正如预期的那样, 的性能是最好的,而 的性能是最差的。
$ g++ naive_mm.cpp -o naive_mm
$ ./naive_mm
C = A * B
Latency: 45.400 ms
C = A^T * B
Latency: 32.500 ms
C = A * B^T
Latency: 57.800 ms
C = A^T * B^T
Latency: 48.300 ms
使用多线程优化的矩阵乘法实现,例如cuBLAS库中的GEMM函数,可以消除四种选项之间的差异。
#include <cassert>
#include <chrono>
#include <cstdint>
#include <functional>
#include <iomanip>
#include <iostream>
#include <tuple>
#include <utility>
#include <vector>
#include <cublas_v2.h>
#include <cuda_runtime.h>
#define CHECK_CUBLAS_ERROR(val) checkCuBlas((val), #val, __FILE__, __LINE__)
template <typename T>
void checkCuBlas(T err, const char* const func, const char* const file,
const int line)
{
if (err != CUBLAS_STATUS_SUCCESS)
{
std::cerr << "cuBlas Runtime Error at: " << file << ":" << line
<< std::endl;
std::exit(EXIT_FAILURE);
}
}
#define CHECK_CUDA_ERROR(val) checkCuda((val), #val, __FILE__, __LINE__)
template <typename T>
void checkCuda(T err, const char* const func, const char* const file,
const int line)
{
if (err != cudaSuccess)
{
std::cerr << "CUDA Runtime Error at: " << file << ":" << line
<< std::endl;
std::cerr << cudaGetErrorString(err) << " " << func << std::endl;
std::exit(EXIT_FAILURE);
}
}
#define CHECK_LAST_CUDA_ERROR() checkCudaLast(__FILE__, __LINE__)
void checkCudaLast(const char* const file, const int line)
{
cudaError_t const err{cudaGetLastError()};
if (err != cudaSuccess)
{
std::cerr << "CUDA Runtime Error at: " << file << ":" << line
<< std::endl;
std::cerr << cudaGetErrorString(err) << std::endl;
std::exit(EXIT_FAILURE);
}
}
float measure_cublas_performance(
std::function<cublasStatus_t(void)> bound_cublas_function,
cudaStream_t stream, int num_repeats = 100, int num_warmups = 100)
{
cudaEvent_t start, stop;
float time;
CHECK_CUDA_ERROR(cudaEventCreate(&start));
CHECK_CUDA_ERROR(cudaEventCreate(&stop));
for (int i{0}; i < num_warmups; ++i)
{
CHECK_CUBLAS_ERROR(bound_cublas_function());
}
CHECK_CUDA_ERROR(cudaStreamSynchronize(stream));
CHECK_CUDA_ERROR(cudaEventRecord(start, stream));
for (int i{0}; i < num_repeats; ++i)
{
CHECK_CUBLAS_ERROR(bound_cublas_function());
}
CHECK_CUDA_ERROR(cudaEventRecord(stop, stream));
CHECK_CUDA_ERROR(cudaEventSynchronize(stop));
CHECK_LAST_CUDA_ERROR();
CHECK_CUDA_ERROR(cudaEventElapsedTime(&time, start, stop));
CHECK_CUDA_ERROR(cudaEventDestroy(start));
CHECK_CUDA_ERROR(cudaEventDestroy(stop));
float const latency{time / num_repeats};
return latency;
}
void print_latency(float latency)
{
std::cout << std::fixed << std::setprecision(3) << "Latency: " << latency
<< " ms" << std::endl;
}
int main()
{
constexpr uint32_t num_repeats{100};
constexpr uint32_t num_warmups{100};
constexpr uint32_t M{256};
constexpr uint32_t K{256};
constexpr uint32_t N{256};
float* A{nullptr};
float* B{nullptr};
float* C{nullptr};
CHECK_CUDA_ERROR(cudaMalloc(&A, M * K * sizeof(float)));
CHECK_CUDA_ERROR(cudaMalloc(&B, K * N * sizeof(float)));
CHECK_CUDA_ERROR(cudaMalloc(&C, M * N * sizeof(float)));
uint32_t const matrix_a_col_major_ld{M};
uint32_t const matrix_a_row_major_ld{K};
uint32_t const matrix_a_transpose_col_major_ld{matrix_a_row_major_ld};
uint32_t const matrix_a_transpose_row_major_ld{matrix_a_col_major_ld};
uint32_t const matrix_b_col_major_ld{K};
uint32_t const matrix_b_row_major_ld{N};
uint32_t const matrix_b_transpose_col_major_ld{matrix_b_row_major_ld};
uint32_t const matrix_b_transpose_row_major_ld{matrix_b_col_major_ld};
uint32_t const matrix_c_col_major_ld{M};
uint32_t const matrix_c_row_major_ld{N};
uint32_t const matrix_c_transpose_col_major_ld{matrix_c_row_major_ld};
uint32_t const matrix_c_transpose_row_major_ld{matrix_c_col_major_ld};
cublasHandle_t cublas_handle;
cudaStream_t stream;
CHECK_CUDA_ERROR(cudaStreamCreate(&stream));
CHECK_CUBLAS_ERROR(cublasCreate(&cublas_handle));
CHECK_CUBLAS_ERROR(cublasSetStream(cublas_handle, stream));
float const alpha{1.0};
float const beta{0.0};
// cublasSgemm assumes column-major matrices.
std::function<cublasStatus_t(void)> const mm_a_col_major_b_col_major_a_b{
std::bind(cublasSgemm, cublas_handle, CUBLAS_OP_N, CUBLAS_OP_N, M, N, K,
&alpha, A, matrix_a_col_major_ld, B, matrix_b_col_major_ld,
&beta, C, matrix_c_col_major_ld)};
std::function<cublasStatus_t(void)> const
mm_a_col_major_b_col_major_a_transpose_b{
std::bind(cublasSgemm, cublas_handle, CUBLAS_OP_T, CUBLAS_OP_N, M,
N, K, &alpha, A, matrix_a_transpose_col_major_ld, B,
matrix_b_col_major_ld, &beta, C, matrix_c_col_major_ld)};
std::function<cublasStatus_t(void)> const
mm_a_col_major_b_col_major_a_transpose_b_transpose{std::bind(
cublasSgemm, cublas_handle, CUBLAS_OP_T, CUBLAS_OP_T, M, N, K,
&alpha, A, matrix_a_transpose_col_major_ld, B,
matrix_b_transpose_col_major_ld, &beta, C, matrix_c_col_major_ld)};
std::function<cublasStatus_t(void)> const
mm_a_col_major_b_col_major_a_b_transpose{std::bind(
cublasSgemm, cublas_handle, CUBLAS_OP_N, CUBLAS_OP_T, M, N, K,
&alpha, A, matrix_a_col_major_ld, B,
matrix_b_transpose_col_major_ld, &beta, C, matrix_c_col_major_ld)};
std::cout << "C = A * B" << std::endl;
float const latency_a_b = measure_cublas_performance(
mm_a_col_major_b_col_major_a_b, stream, num_repeats, num_warmups);
print_latency(latency_a_b);
std::cout << "C = A^T * B" << std::endl;
float const latency_a_transpose_b =
measure_cublas_performance(mm_a_col_major_b_col_major_a_transpose_b,
stream, num_repeats, num_warmups);
print_latency(latency_a_transpose_b);
std::cout << "C = A * B^T" << std::endl;
float const latency_a_b_transpose =
measure_cublas_performance(mm_a_col_major_b_col_major_a_b_transpose,
stream, num_repeats, num_warmups);
print_latency(latency_a_b_transpose);
std::cout << "C = A^T * B^T" << std::endl;
float const latency_a_transpose_b_transpose = measure_cublas_performance(
mm_a_col_major_b_col_major_a_transpose_b_transpose, stream, num_repeats,
num_warmups);
print_latency(latency_a_transpose_b_transpose);
CHECK_CUDA_ERROR(cudaFree(A));
CHECK_CUDA_ERROR(cudaFree(B));
CHECK_CUDA_ERROR(cudaFree(C));
CHECK_CUBLAS_ERROR(cublasDestroy(cublas_handle));
CHECK_CUDA_ERROR(cudaStreamDestroy(stream));
}
使用高度优化的实现,四种选项之间几乎没有差异。
$ nvcc cublas_mm.cu -o cublas_mm -lcublas
$ ./cublas_mm
C = A * B
Latency: 0.008 ms
C = A^T * B
Latency: 0.010 ms
C = A * B^T
Latency: 0.009 ms
C = A^T * B^T
Latency: 0.008 ms
参考文献
-
Row- and Column-Major Order – Wikipedia(https://en.wikipedia.org/wiki/Row-_and_column-major_order)
(文:GiantPandaCV)

