CVPR 2025｜MetricGrids：基于泰勒展开的任意非线性特征网格神经表征

论文标题： MetricGrids: Arbitrary Nonlinear Approximation with Elementary Metric Grids based Implicit Neural Representation

论文地址： https://arxiv.org/abs/2503.10000

Github： https://github.com/wangshu31/MetricGrids

背景：

隐式神经表示（Implicit neural representations，INRs）已成为信号表示的新范式，在重建各种信号方面表现出卓越的性能，包括二维图像、三维视频、三维形状和辐射场等。INRs利用神经网络通过使用规则采样的信号值作为训练数据并优化网络参数来建立连续坐标与目标输出之间的映射。许多隐式神经表示方法依赖于大型的多层感知机（MLP）作为基线，但受到频谱偏差的限制。

为了提高信号重建精度，混合表示，或称为基于网格的神经表示在信号输入域离散的顶点坐标处存储信号的潜在空间特征，并使用解码器重建目标信号值。为了表示复杂的细节，混合表示需要在整个信号输入域建立一个密集的特征网格，以确保基于存储的点可以高精度地获得连续空间点的特征。特别地，考虑到不同信号在空间的复杂性和稀疏性各不相同，基于规则网格的表示往往导致较大的存储需求和冗余。目前已有高效的网格结构实现，如通过启发式策略进行剪枝和合并、使用低秩张量、使用自适应径向基函数等。然而如何有效地用离散网格表示连续空间的非线性信号尚未得到充分研究。

研究内容：

鉴于上述挑战，我们首先研究了使用特征网格结构进行信号逼近的机制，并指出依赖线性插值的规则网格隐含地将潜在特征空间限制为分段线性形式，这是非线性信号的一种退化情况。为解决这一问题，我们提出了MetricGrids，基于泰勒展开的概念在不同度量空间中构建多个特征网格，作为信号潜在特征空间的高阶近似。进一步，我们采用多个长度的哈希编码分别存储这些特征网格，以探索高阶导数的稀疏性，从而保持模型的紧凑性。最后，考虑如何充分利用不同阶项的特征，实现复杂的非线性变换的同时减少所需网格的数量，设计了高阶外推解码器基于学习到的特征网格逐步生成更高阶项。

建模分析：

隐式神经表示可以理解为信号输入到输出的映射，该映射使用神经网络参数化： ，其中  分别表示坐标和重建的信号值， 表示可学习参数，对应于 MLP 参数。对于混合表示，该映射可以进一步表示为编码－解码架构：  。其中，从网格中索引特征视作编码，将特征转换到信号域视作解码，可学习参数包含一个特征网格和解码器参数  是索引函数，用于连续信号在特征网格中插值特征，依赖于距离度量  。从信号表示的角度看，特征网格可以被看作是连续信号的一个离散特征表示。然而，自然场景通常复杂且高度非线性，同样反映在特征空间中。现有方法使用一个分段线性近似的退化特征空间重建信号，在复杂区域自然产生了挑战。

鉴于连续函数的任何点都可以通过泰勒展开用包含不同阶项的多项式在其邻近点近似，网格中的任何点也可以通过一系列基本度量网格来近似。每个基本度量网格包含了导数相关信息，如同泰勒展开中的不同阶项，点与点之间的距离是用不同阶的度量计算。这样一来，经过索引函数后，每个特征网格提供了类似形式的特征，与泰勒展开中每一阶项的形式相对应。

方法介绍：

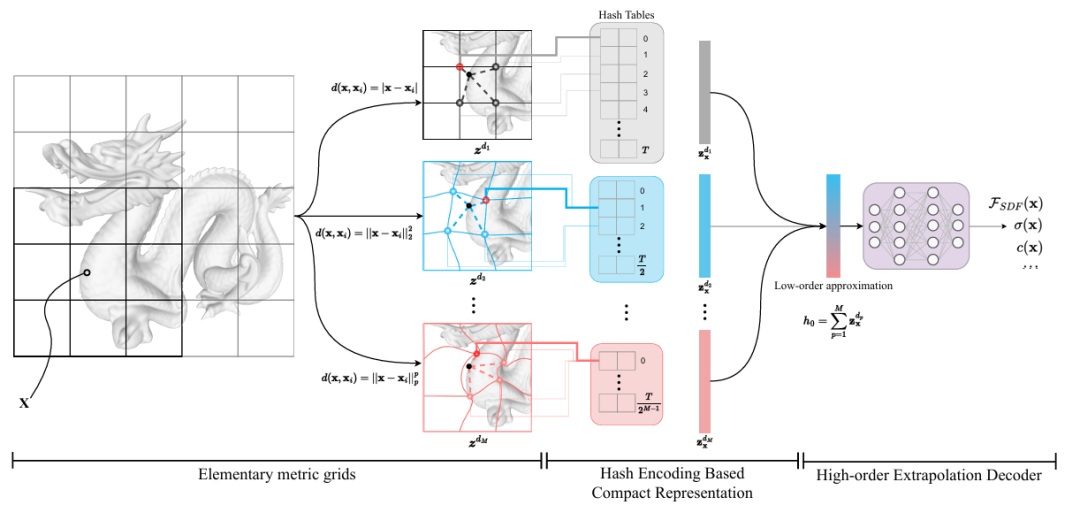
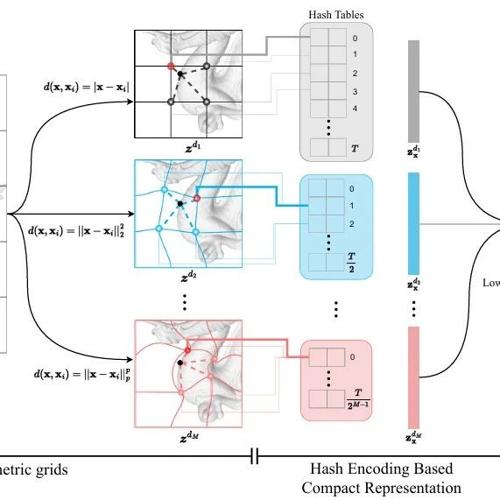
1. 基本度量网格（Elementary Metric Grids）：正如前文分析所述，在不同的非线性度量空间中建立特征网格，并按照泰勒展开的多项式和形式聚合，可以得到信号的非线性潜在特征。使用不同距离度量建立的特征网格  ，其中  表示具有离散顶点坐标的网格结构，每个坐标存储一个可学习特征向量； 表示定义在该网格上的距离度量。为了与泰勒展开公式保持一致，不同阶度量可使用指数形式的 P 范数。于是，神经表示的编码过程重写为  。通过基于梯度的优化过程，不同基本度量网格中学习到不同阶导数的特征。其中第一个网格中的特征  使用线性距离，与现有的范式保持一致， 则提供非线性近似。

2. 基于哈希编码的压缩（Hash Encoding Based Compact Representation）：相较于I-NGP等现有方法，MetricGrids使用了多个特征网格提高潜在特征空间的非线性拟合能力，导致参数量翻倍。为此，我们基于Instant-NGP的启发使用哈希编码对基本度量网格进行压缩表示。需要注意的是，不同度量网格中存储的是不同阶导数，因此需要将其隔离，避免在不同阶数的特征中产生哈希冲突。另一方面，在信号的平滑区域，不同阶导数均为零，因此高阶导数比低阶导数更加稀疏。因此为高阶度量网格设置更短的哈希表长度 T 有进一步提高紧凑性。因此，对于一个顶点坐标  ，我们使用哈希映射索引度量网格特征： ，其中  。  表示按位异或操作，是唯一的大质数，与 Instant－NGP 相同。

3.高阶项外推解码器：为了减少学习到的网格数量并提高基本度量网格的表示效率，实际只采用了三个度量网格。为了进一步减少阶数有限导致的近似误差，我们进一步设计了高阶项外推解码器，充分利用存储在网格中的线性和相对较低阶项逐步生成高阶项。

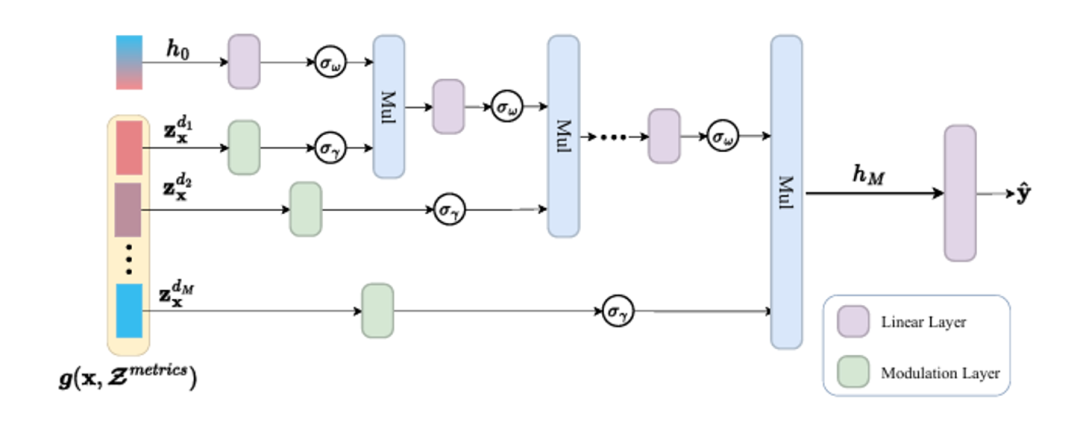
对网格特征  ，根据泰勒公式进行求和作为基础的低阶特征。在解码器中，每一层添加额外的调制层，将基本度量网格中从低阶到高阶的导数诱导特征通过哈达玛积注入解码器，生成一个更高阶项。不考虑激活函数，经过  个解码器层后特征阶数为  ，相较于初始的 m 阶近似特征非线性特征更强。经过输出层将高阶特征转换到输出域，即可得到重建的信号。

实验结果：

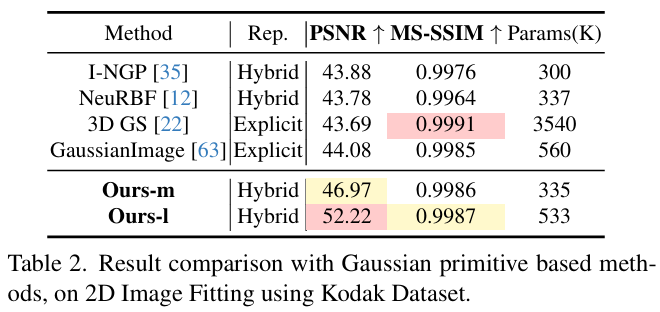
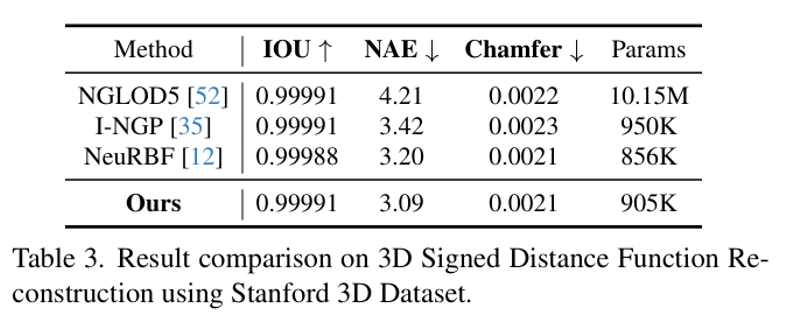
本文所提出的MetricGrids在2D图像、3D有向距离场、5D辐射场重建中均取得了最好的重建精度。

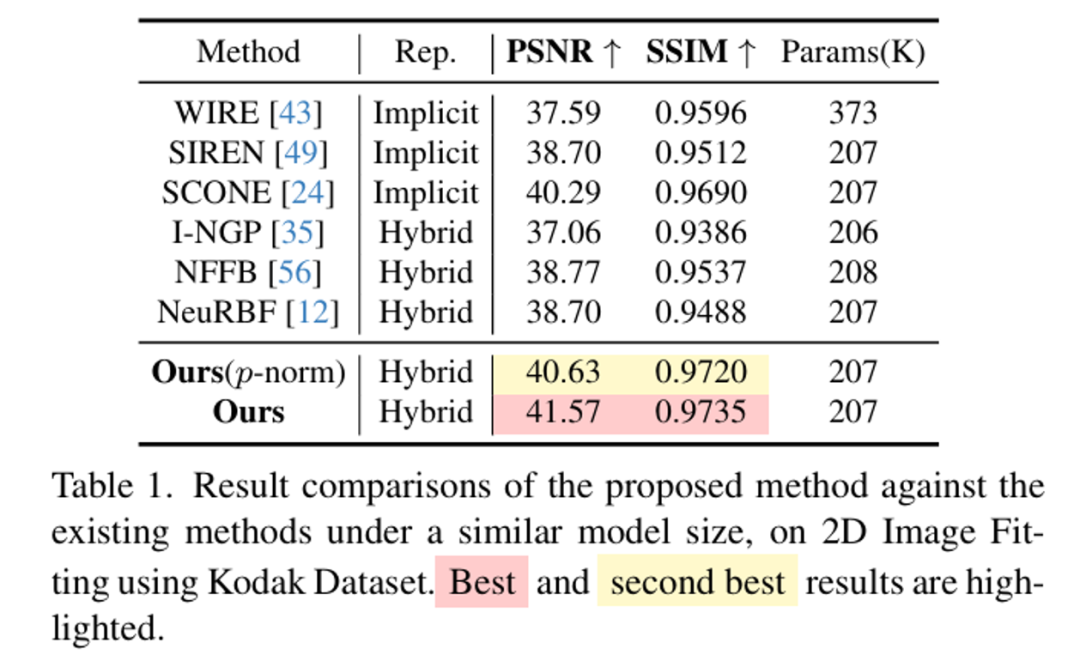
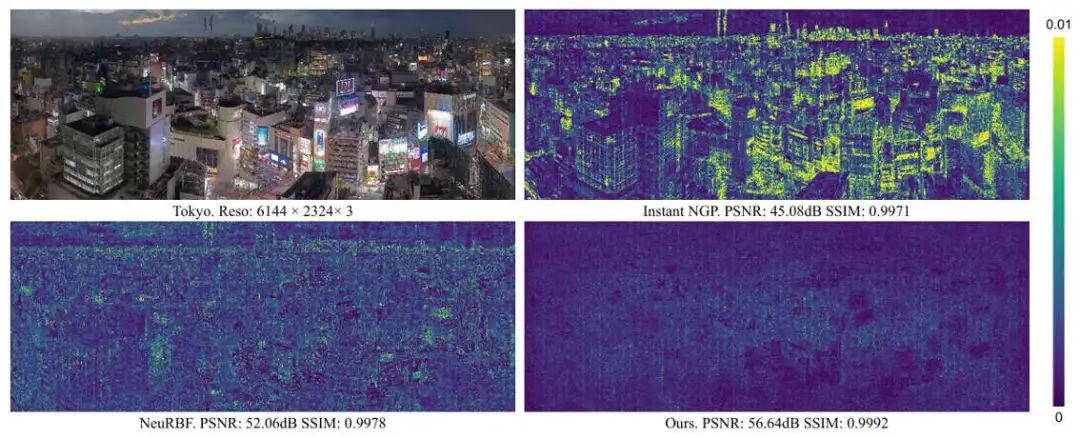
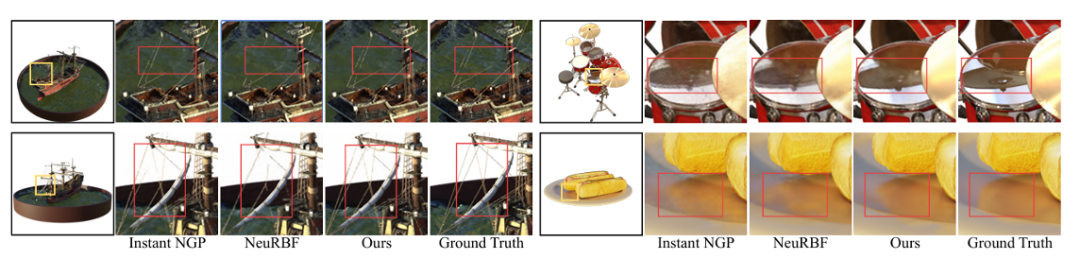
从大型图像重建的L2误差图中可以看出，MetricGrids能够有效提升边缘和复杂纹理处的重建质量，体现了非线性特征空间的有效性。

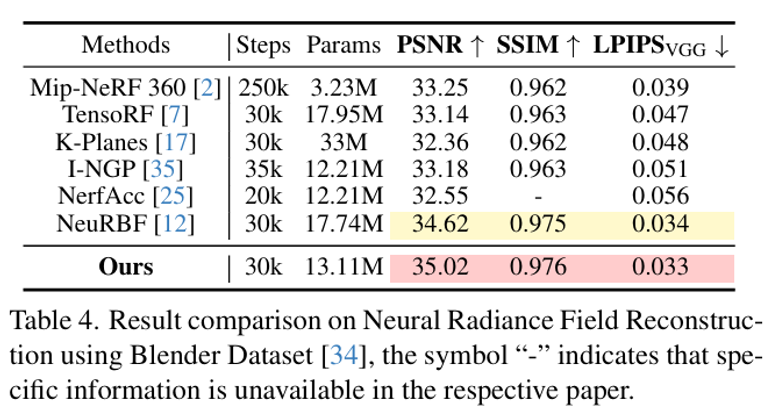
在辐射场重建任务中，MetricGrids对于反光表面和精细的几何结构重建质量也明显优于基线和现有方法。

为了更进一步验证文中所提方法的有效性，我们还在Kodak和Stanford 3D数据集上进行了多项消融实验：

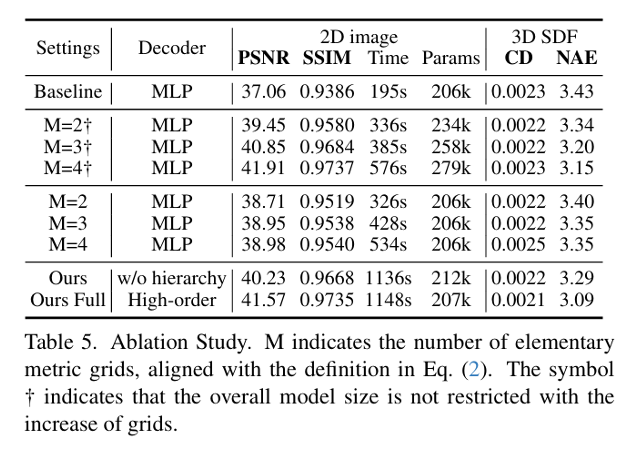
首先我们通过不同数量的基本度量网格验证了非线性度量带来的拟合精度提升。进一步，我们通过限制参数量与基线相当验证MetricGrids的参数效率。当阶数更高时，需要将分辨率和哈希表长度参数适当缩小以维持参数量不变。从表5的第二部分中可以看出，参数量固定的情况下添加一个高阶项网格有效地提高了性能，证明了通过度量网格进行非线性插值在表示质量方面比线性插值提供了更好的归纳偏差。然而，当高阶项的数量超过三个时，性能增益减小，表明显式存储高阶项在计算上效率低下。最后，我们评估了解码器是否采用逐步输入不同阶度量网格特征的作用。从表5的最后一部分可以看出，调制层结构能够提升解码器性能，但MetricGrids逐步注入的方式能够有效地利用多个度量网格的信息来提升最终性能。

结论：

我们提出了MetricGrids，它为各种信号类型提供了准确的神经表示。我们的分析揭示，当前基于网格的神经表示中使用线性索引函数来获取连续空间点特征，导致潜在空间的退化，从而在非线性信号上产生参数效率低下和近似误差。基于泰勒展开思想我们提出了一种在非线性度量空间中定义的基本度量网格作为高阶项特征来捕捉复杂的潜在空间非线性，并进一步使用哈希编码和高阶外推解码器以提高拟合精度，而不增加参数和存储需求。实验结果表明，我们的方法显著优于基线模型，并在2D图像拟合、3D形状拟合以及神经辐射场重建任务中实现了最先进性能。