作者：Leila Sloman
机器之心编译
一切始于一场赌局。
20 世纪 80 年代末，在洛桑的一次会议上，两位数学家 Noga Alon 和 Peter Sarnak 展开了一场友好的辩论。两人当时都在研究由节点和边组成的集合即图，他们特别想更好地理解一种名为「扩展图」的看似矛盾的图类型，这种图的边相对较少，但仍然高度互连。
争论的焦点在于最优扩展图：那些连通性尽可能强的扩展图。Sarnak 认为这样的图很少见，他和两位合作者很快发表了一篇论文，运用数论中的复杂思想来构建示例，并指出任何其他结构都同样难以实现。
而 Alon 则寄希望于随机图通常展现出各种最优性质的事实，他认为这些极其优秀的扩展图会很常见。如果你从大量可能性中随机选择一个图，则几乎可以保证它是一个最优扩展图。
左为 Peter Sarnak，右为 Noga Alon。
如今，Sarnak 和 Alon 是普林斯顿大学的同事。几十年来，这场赌局的细节已经变得模糊不清。「当时并不太严肃，」Alon 回忆道，「我们甚至对赌局的内容都意见不一。」
尽管如此，这个传说依然流传，它微妙地提醒着数学家们，究竟谁才是对的。
最近，三位数学家通过探究物理学中一个关键现象，并将其推向极限，最终对这场赌局做出了裁决。他们两人都错了。
-
论文标题： Ramanujan Property and Edge Universality of Random Regular Graphs
-
arXiv 地址：https://arxiv.org/pdf/2412.20263
扩展的极限
自 20 世纪 60 年代数学家开始研究扩展图以来，它们就被用于大脑建模、统计分析和构建纠错码。由于扩展图的边数极少，因此效率极高。同时，由于扩展图高度连通，因此仍然能够抵御潜在的网络故障。Sarnak 表示，这种矛盾「使得扩展图既违反直觉，又非常有用」。
因此，数学家们想要更好地理解它们。「减少边数」和「增加图的连通性」之间的这种矛盾可以延伸到多远？以及在张力最高的好的扩展图有多普遍？
为了回答这些问题，研究人员需要精确地定义扩展图。有很多方法可以做到这一点，其中一种是：为了将扩展图拆分成两个独立的部分，你需要擦除许多边。另一种是：如果你沿着图的边缘徘徊，在每一步随机选择方向，你很快就能探索整个图。
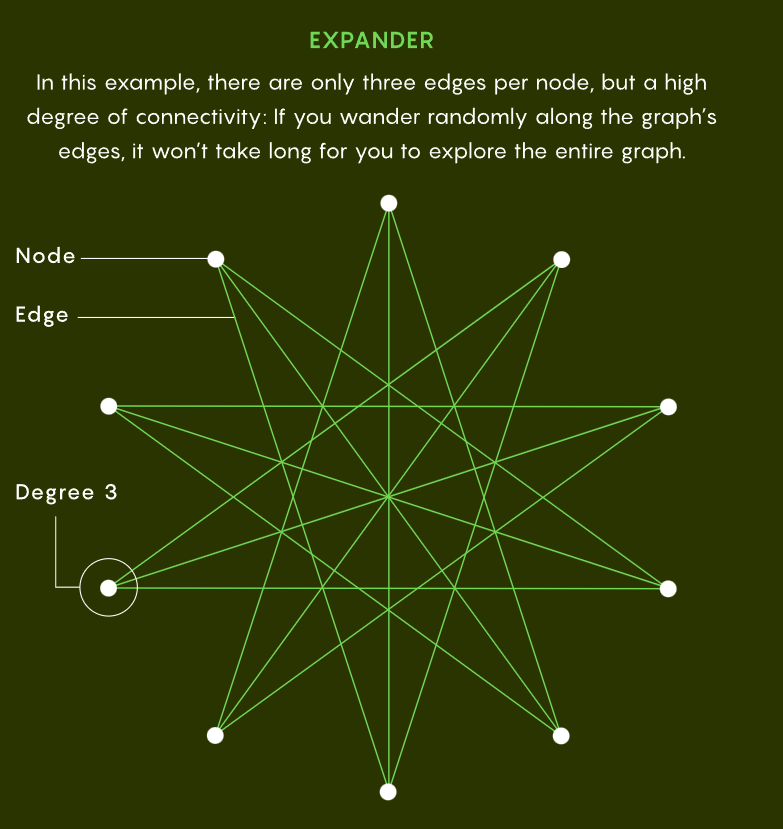
下图为扩展图示例，每个节点只有三条边，但连通性很高。如果你沿着图的边随机游走，那么探索整个图不需要花费很长时间。
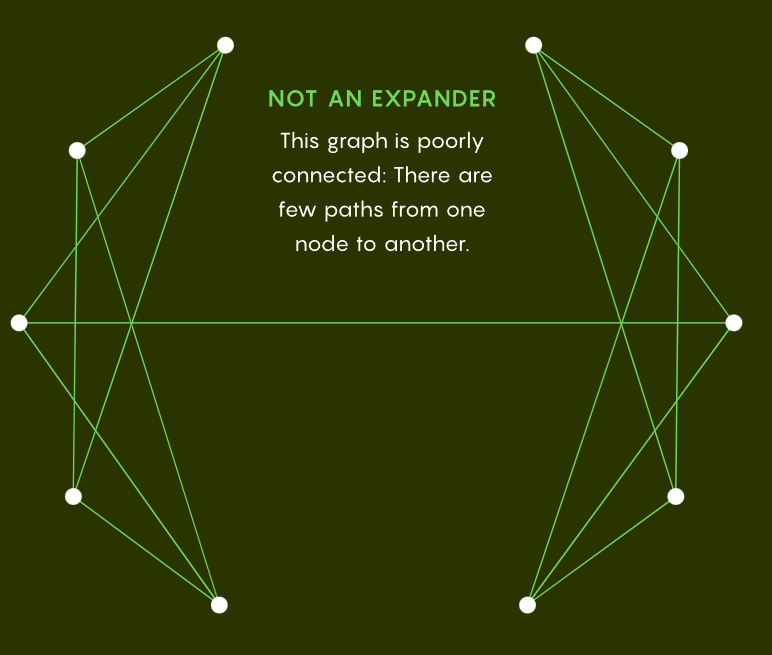
下图为非扩展器示例，该图连通性较差，从一个节点到另一个节点的路径很少。
1984 年，数学家 Józef Dodziuk 证明，所有这些扩张度量都通过一个量联系起来 —— 至少对于某些类型的图而言是如此。在这些所谓的「正则图」中，每个节点都有相同数量的边，这确保了整个图的边数相对较少。因此，要使其成为扩展图，你只需证明它是连通的。这就是 Dodziuk 数（quantity）的来源。
要计算这个数，你必须首先构造一个由 1 和 0 组成的数组，称为邻接矩阵。这个邻接矩阵表示图中哪些节点通过边连接，哪些节点没有通过边连接。
然后，你可以使用该矩阵计算一系列数字，称为特征值（eigenvalues），这些数字可以提供有关原始图的有用信息。例如，最大的特征值给出了连接到图中每个节点的边数。Józef Dodziuk 发现，第二大特征值可以告诉你图的连通性。该数字越小，图的连通性越好 —— 这使得它成为一个更好的扩展图。
在 Józef Dodziuk 发现之后不久，Alon 和另一位数学家 Ravi Boppana 证明，如果正则图中的每个节点都有 d 条边，则第二个特征值不可能比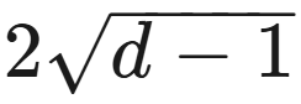 
小很多。第二个特征值接近「Alon-Boppana 界限」的正则图是一个良好的扩展图；相对于具有相同边数的其他正则图，它的连通性良好。但是，如果第二个特征值实际上达到了界限，那么该图就是可以想象到的最优扩展图。
对于包括 Sarnak 在内的一些数学家来说，「Alon-Boppana 界限」是一个令人着迷的挑战。他们想知道：能否构建达到这个极限的图？
随机性赌博
在 1988 年发表的一篇具有里程碑意义的论文中，Sarnak、Alexander Lubotzky 和 Ralph Phillips 斯找到了方法。他们利用印度数学天才 Srinivasa Ramanujan 在数论领域取得的一项高超技术成果，构建了满足「Alon-Boppana 界限」的正则图。
因此，他们将这些最优扩展图称为「拉马努金图」（Ramanujan graphs）。（同年，Grigorii Margulis 使用了不同但同样高超的方法构建了其他示例。）
论文地址：https://link.springer.com/article/10.1007/BF02126799
新泽西州普林斯顿高等研究院的 Ramon van Handel 表示：「直观地看，你似乎可以预料到构建拉马努金图几乎难以实现的难度。并且看起来，最优图应该非常难以实现。」
但在数学中，难以构造的事物往往出奇地常见。「这是数学界的普遍现象，」van Handel 说。「任何你能想象的例子都不会具备这些属性，但一个随机的例子却会。」
包括 Alon 在内的一些研究人员认为，拉马努金图或许也适用同样的原理。Alon 认为，寻找这些图所需的巨大努力与其说是物质的丰富性，不如说更多地反映了人类的思维方式。这种信念促成 Sarnak 和 Alon 的赌局：Sarnak 打赌，如果把所有正则图都收集起来，其中只有极小一部分是拉马努金图；而 Alon 则认为几乎所有图都是拉马努金图。
很快，关于 Sarnak 和 Alon 打赌的传闻就在社区里流传开来，尽管人们对当时的记忆各不相同。「说实话，这更像是民间传说，」Sarnak 承认道，「我其实不记得那件事了。」
几十年后，在 2008 年，对大量正则图及其特征值的分析表明，答案并非一目了然。有些图符合拉马努金定理，有些则不然。这只会让找出确切的比例变得更加艰巨。
在证明一个适用于所有图（或所有图都不适用）的性质时，数学家们拥有丰富的工具箱。但要证明某些图符合拉马努金定理，而其他图则不然，则需要精确度，而图论学家们并不确定这种精确度从何而来。
后来发现，在一个完全不同的数学领域，一位名叫姚鸿泽（Horng-Tzer Yau）的研究员正在解决这个问题。在花了十多年时间研究与随机图相关的矩阵之后，姚鸿泽解决了一个有关它们行为的重大难题。
姚鸿泽
一个「疯狂」的想法
在图论研究者还在努力理解 2008 年那项研究的意义时，哈佛大学教授姚鸿泽已经沉迷特征值问题好几年了。他研究的特征值来源于更广泛的一类矩阵，这些矩阵的元素是通过随机方式生成的 —— 比如抛硬币或进行其他随机过程。姚鸿泽想弄清楚：使用不同的随机过程，矩阵的特征值会如何变化。
这个问题可以追溯到 1955 年，当时物理学家 Eugene Wigner 使用随机矩阵来模拟像铀这样重原子中原子核的行为。他希望通过研究这些矩阵的特征值，来了解系统所具有的能量。
很快，Wigner 注意到一个奇怪的现象：不同的随机矩阵模型的特征值似乎都呈现出相同的分布模式。对于任何一个随机矩阵，每个特征值本身也是随机的 —— 你选定一个数值区间，某个特征值落在这个区间内的概率是可以计算的。但神奇的是，这种概率分布似乎与矩阵的具体构造无关：无论一个随机矩阵的元素只是由 1 和 −1 组成，还是可以是任意实数，其特征值落入某个区间的概率都几乎不变。
Eugene Wigner
Wigner 在他研究的各种随机系统中，观察到了出人意料的普遍行为。如今，数学家们已经将这种行为的适用范围进一步拓展。
Wigner 曾猜想，任何随机矩阵的特征值都应遵循相同的概率分布。这个预测后来被称为普遍性猜想。
姚鸿泽表示这个想法太过疯狂，导致很多人根本不相信他说的是真的。但随着时间推移，他和其他数学家不断证明，这一猜想在许多不同类型的随机矩阵中都成立。一次又一次，Wigner 的理论被证实是正确的。
姚鸿泽开始思考，自己还能将这一猜想推进多远。他想寻找那些能突破对标准矩阵理解的问题。
于是，在 2013 年，当 Sarnak 提出让他研究与随机正则图相关的矩阵的特征值时，他接受了这个挑战。
如果姚鸿泽能证明这些特征值也满足普遍性猜想，那么他就能掌握它们的概率分布。接下来，他就可以利用这些信息来计算第二特征值达到 Alon–Boppana 界限的概率。
换句话说，他将能够为 Sarnak 和 Alon 的赌局 —— 有多少比例的正则图是拉马努金图 —— 给出一个明确答案。
于是，他开始动手了。
快要成功了
许多类型的随机矩阵，包括曾启发 Wigner 提出普适性猜想的那些矩阵，本身具备一些良好性质，使得人们可以直接计算它们的特征值分布。然而，邻接矩阵并不具备这些性质。
大约在 2015 年，姚鸿泽与他的研究生黄骄阳（2010-201 年在清华大学交叉信息研究院计算机科学实验班学习）以及另外两位合作者提出了一项计划。首先，他们将使用一个随机过程，对邻接矩阵中的元素做出微小调整，从而得到一个新的随机矩阵，这个矩阵具备他们所需的那些良好性质。
接着，他们将计算这个新矩阵的特征值分布，并证明它满足普遍性猜想。
最后，他们还要证明，这些所做的调整足够小，不会影响原始邻接矩阵的特征值 —— 这就意味着，原始邻接矩阵也满足普遍性猜想。
黄骄阳在概率论领域的研究，使他涉足了数学、物理与计算机科学中的多个难题。
2020 年，黄博士毕业后，他与合作者终于能够借助这一方法，将普遍性猜想扩展到一定规模的正则图。只要图的边数足够多，它的第二特征值就会呈现出几十年前 Wigner 研究过的那种分布。但要解答 Alon 和 Sarnak 之间的赌约，仅仅证明一部分正则图还不够 —— 他们需要对所有正则图都证明这一猜想成立。
到了 2022 年秋天，一位名叫 Theo McKenzie 的博士后研究员来到哈佛大学，希望深入了解黄骄阳、姚鸿泽及其合作者在 2020 年证明中使用的工具和方法。他有很多内容需要「补课」。「我们已经在这个问题上钻研了很长时间」姚鸿泽说。
但加州大学伯克利分校的数学家、McKenzie 的前博士导师 Nikhil Srivastava 表示，McKenzie 非常无畏，他并不害怕去攻克这些非常棘手的问题。
在花了几个月时间深入研究黄骄阳和姚鸿泽的方法后，McKenzie 终于做好准备，能够以新的视角和力量加入进来。「你希望有人能检查大量细节，并提出各种不同的问题，」姚鸿泽说，「有时候，你就是需要更多人手。」
一开始，这三位数学家只能取得部分结果。他们还无法精准地完成证明策略中的第二步 —— 计算经过微调的矩阵的特征值分布，因此还不足以证明所有正则图都满足普遍性猜想。但他们已经能够证明，这些特征值仍然满足一些关键性质，而这些性质强烈暗示：这个猜想极有可能成立。
McKenzie 是最后一位加入这个数学家团队的成员 —— 他们解决了一个关于所谓拉马努金图的争论，这个问题已经悬而未决了数十年。
「我知道他们已经接近彻底解决这个问题的边缘了。」Sarnak 说。
而事实证明，在另一项研究中，黄骄阳其实早已在尝试他们最终所需的那一关键要素。
闭合循环
黄骄阳正在独立研究一组被称为「循环方程（loop equations）」的数学公式，这些方程描述了随机矩阵模型中特征值的行为。他意识到，如果他、McKenzie 和姚鸿泽能够证明他们的矩阵足够精确地满足这些方程，那就能补上他们在第二步推理中所缺失的信息。
他们最终确实做到了。经过数月细致入微的计算，他们完成了证明。所有的正则图都遵循 Wigner 普遍性猜想：随机选取一个正则图，它的特征值将呈现出已知的那种分布形式。
这也意味着，这三位数学家现在已经知道第二特征值取值的具体分布情况。他们可以进一步计算出，有多少比例的第二特征值达到了 Alon-Boppana 界限 —— 也就是说，有多少比例的随机正则图是完美扩展图。三十多年后，Sarnak 和 Alon 终于得到了他们打赌的答案。这个比例大约是 69%，这意味着这些图既不算常见，也不算稀有。
最先得知这个消息的是 Sarnak。黄骄阳说：「他告诉我们，这是他收到过的最棒的圣诞礼物。」他笑着补充道：「所以我们觉得一切都值得了。」
这一结果也表明，普遍性猜想比研究者原先预想的更加广泛且强大。数学家们希望继续突破这一猜想的适用边界，并利用这次新证明中的技术来解决相关问题。
而与此同时，他们也可以稍稍放松一下，享受在神秘莫测的拉马努金图宇宙中，又多掌握了一点点知识的喜悦。
「我们两个其实都不太对，」Alon 说道。「不过，我还是稍微更接近正确一些，因为这个概率超过了一半。」他笑着补充道。
（文：机器之心）