极市导读
文章详细介绍了FlashAttentionV3(FA3)的前向过程原理,结合代码分析了其数学公式和工程实现的细节,包括分块计算、在线softmax的实现以及splitK部分的优化,旨在帮助读者更好地理解FA3的高效实现方式。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
前言
接着Kernel系列,前文介绍了PagedAttentionV1和V2,本文开始介绍FlashAttentionV3 (后文简称为FA3)。FA3的涉及内容比较多,如果用一篇来介绍的话,内容太大,不便于阅读,所以初步会分为《FA3原理篇》,《FA3数据的Load和Store篇》,《FA3的WGMMA数据划分和Mask设计篇》,《FA3的Block调度,负载均衡,以及Overlap技巧篇》。同时分析FA系列,cutlass是必不可少,所以计划有Cutlass基础篇的四篇,分别是《cutlass核心数据结构和函数篇》,《理解cutlass的MMA/WGMMA数据划分篇》,《cutlass的数据加载之TMA设计与使用篇》,《cutlass中的Warp Specialization(即WS)编程模式篇》。另外针对GPU优化的基础知识介绍一下《CPU与GPU指令调度和优化思路的差异篇》。文章的名以最终发布为准。
为啥把这篇作为FA3系列的开篇,主要原因是理解了数学原理,对看懂整体的代码起到提纲挈领的作用。介绍FlashAttention数学原理的文章很多,大部分都讲的挺好,不同于前人的文章,本文主要是结合代码,拉近数学公式和工程实现的距离,让大家可以独立看懂FlashAttention的代码。其实在笔者之前的文章中有过相应FlashAttentionV2和RingAttention公式推导的介绍,原理上FA3相比FA2并没有变化,表述方式上,本文结合代码进行了更加细致介绍以及增加了对splitK部分(combine_attn_seqk_parallel)介绍。本文或者是接下来的系列文章是基于FlashAttention的0dfb28174333d9eefb7c1dd4292690a8458d1e89提交来介绍的,如果有讲的不对或者不理解的地方,欢迎留言探讨。
前面文章可参考:
杨鹏程:聊聊CUDA编程中线程划分和数据分块 之 PagedAttention(V1/V2)分析
https://zhuanlan.zhihu.com/p/710310530
杨鹏程:从Coding视角出发推导Ring Attention和FlashAttentionV2前向过程
https://zhuanlan.zhihu.com/p/701183864
简介
先回顾一下FlashAttention主要解决什么问题,或者说Flash的含义。FlashAttention是对经典SelfAttention的一种高效实现,如下图,展示的是经典的SelfAttention计算过程(去除了所有的可并行的维度,不包括GQA优化),主要解决的问题分为下面几个层次:
-
解决空间复杂度的中间激活的显存占用问题,如下图中的的中间结果;
-
将片上资源(shared memory)与序列长度解耦,可以实现超长序列的SelfAttention,早期的FasterTransformer以及PagedAttentionV1(V2通过SplitK来解决这个问题,详情可以参看笔者前一篇关于PagedAttentionV1/V2的介绍)就没有解决这个问题。
那FlashAttention如何解决这两个问题呢,谈到这个问题,就绕不开下面这张图:
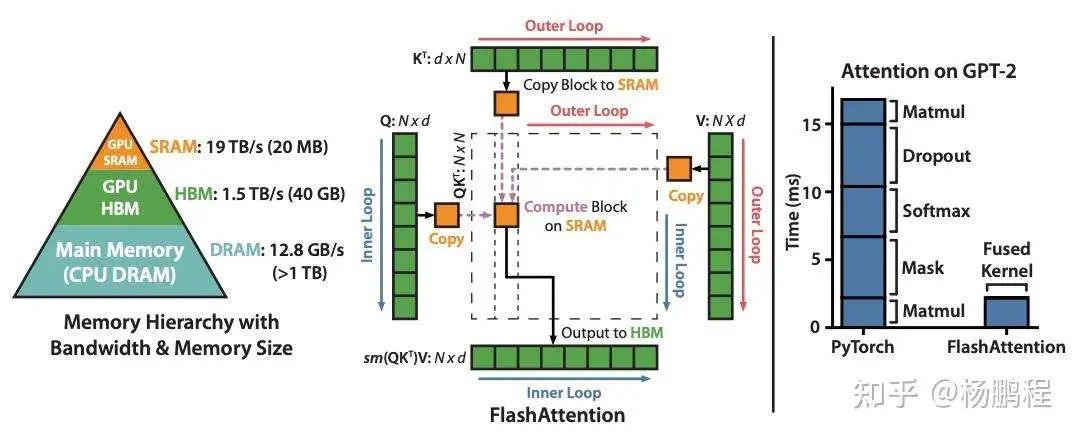
上图描述的是FlashAttentionV1的计算逻辑,通过对 ,在序列维上的划分,来实现片上一次只需要计算一部分固定序列长度的 ,将片上资源与真实序列长度的解耦,这样无论多长的序列,只要 可以放到显存上(甚至不需要在显存上),都可以完成 SelfAttention的计算。这个思想其实在GEMM里早有运用,在SelfAttention中应用较晚,主要是SelfAttention多了一个Softmax操作,对分块Softmax的等效计算,也就是Online Softmax是在后面提出的。另外在2021之前,既懂CUDA/cutlass和GPU架构,又懂online softmax的人并不多,所以很多人没意识到在Kernel内做这个工作,其实Kernel外,在 FlashAttention之前已有相关工作。
理解"Flash",这个点可能很多人知道,但是由于比较重要,这里再强调一下。由于分块计算,单个块的 的计算过程,如上面的图一,都可以在片上完成,消除Global memory的写入和写出,从而获得更好的性能。部分人的理解都到此为止,其实这里面还有两个更深的层次:
1.FA1并不是完全的片上计算的,如上图所示, 是在外层循环,在内层循环,所以一块 对应的 的全量,那么中间的 就是一个全尺寸大小,与全尺寸的 大小相同,这个尺寸是相当大的,尤其是序列很长时,所以 不可能保存在片上,而是写到Global Memory上了,整个过程并不是都在片上的。到了FA2, 放到了外循环, 变成内循环,此时一个分块的 ,完成了所有分块 ,即得到最终的结果分块 ,与内循环 的计算结果可以一直复用 ,可以保证 一直在片上,甚至一直在寄存器上(FA3在store的时候为了用TMA,这里可以选择把O写到Shared Memory上)。
2.第二层,会被很多人忽略,不研究代码可能也不会在意到这个点。这个点需要对mma指令的数据layout有了解才行,这里简单说明,详细内容会在《FA3的WGMMA数据划分和Mask设计篇》中介绍。例如mma的数据layout:MxNxK ,A矩阵shape:MxK ,B矩阵的shape为 ,对 进行reduce,得到 ,其中 是 的序列维, 是 的序列维,对mma指令的输出结果,一个确定 Q token,对应的序列维 的所有结果都在一个quarter warp内,即:一个local softmax的所有计算元素都在一个quarter warp内。这样softmax的计算以及后面 的计算,都在一个warp内,这样就没有warp之间的通信,不需要把中间结果写到 shared memory上,从而实现了完全的寄存器操作,取得"Flash"效果。当然还有很多比较重要的优化点,将在后面文章中展开。这部分啰嗦的有点多,后面直接切入正题。
主逻辑数学原理
符号约定
-
表示代码中的 row_max ; -
表示代码中的 row_sum ; -
或者 表示 scores 为 的输出激活; -
上标. 表示当前分块; -
上标: 表示所有的历史分块,相当于省略了 ;
函数公式化
代码中主要涉及函数如下,注意代码中有融合了 scale ,这里简化了,另外FA3复用了FA2的优化,将 exp 运算转化为 (主要考虑到 有更多的算力单元),为了简化表述这里直接使用 表示:
-
reduce_max :zero_init=true : ,zero_init=false : ;false时会求历史最大; -
scale_apply_exp2 ,in place操作; -
reduce_sum :zero_init=true : ,zero_init=false : ,这里的false是和 reduce_max 相同的,求和值包括历史的 。
注意:FA3的online softmax计算依然是采用分子和分母分开的方式,下文中说到的softmax的scores值,均是指softmax的分子。
第一个分块
softmax.template online_softmax</*Is_first=*/true>(tSrS);
代码展开:
template<bool Is_first, bool Check_inf=false, typename Tensor0>
__forceinline__ __device__ TensorT online_softmax(Tensor0 &acc_s) {
...
flash::template reduce_max</*zero_init=*/true>(scores, row_max);
flash::template scale_apply_exp2</*Scale_max=*/true, /*Check_inf=*/true, Use_max_offset>(scores, row_max, softmax_scale_log2);
flash::reduce_sum</*zero_init=*/true, /*warp_reduce=*/false>(scores, row_sum);
...
};
对应的公式有:
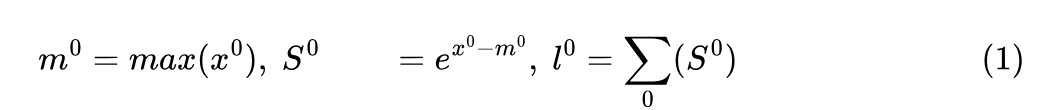
其中的warp_reduce是一个小的优化点,由于只有最后阶段才会使用,所以前期计算不需要reduce,而是保存在各线程的寄存器上,到最后的finalize函数进行求和。
第i个分块
clear(scores_scale);
#pragma unroll 1
for (; n_block > n_block_min; --n_block) {
...
softmax.rescale_o(tOrO, scores_scale);
...
cute::copy(softmax.template max</*Is_first=*/false, /*Check_inf=*/Is_local>(tSrS), scores_scale);
softmax.template online_softmax</*Is_first=*/false, /*Check_inf=*/Is_local>(tSrS);
...
}
...
softmax.rescale_o(tOrO, scores_scale);
...
cute::copy(softmax.template finalize</*Is_dropout=*/false, Is_split>(tSrS), scores_scale);
...
softmax.rescale_o(tOrO, scores_scale);
其中softmax.rescale_o(tOrO, scores_scale);是将调整系数scores_scale以in place的方式作用到上。cute::copy(softmax.template max</*Is_first=*/false, /*Check_inf=*/Is_local>(tSrS), scores_scale)使用当前的分块scores来更新scores_scale值和值。代码如下:
template<bool Is_first, bool Check_inf=false, typename Tensor0>
__forceinline__ __device__ TensorT max(Tensor0 &acc_s) {
...
Tensor scores_max_prev = make_fragment_like(row_max);
cute::copy(row_max, scores_max_prev);
flash::template reduce_max</*zero_init=*/false>(scores, row_max);
#pragma unroll
for (int mi = 0; mi < size(row_max); ++mi) {
float scores_max_cur = !Check_inf
? row_max(mi)
: (row_max(mi) == -INFINITY ? 0.0f : row_max(mi));
scores_scale(mi) = exp2f((scores_max_prev(mi) - scores_max_cur) * softmax_scale_log2);
row_sum(mi) *= scores_scale(mi);
}
...
return scores_scale;
};
可以发现 max 函数会将历史的最大值 保存起来,同时通过调用 reduce_max 函数求的包括当前分块在内,截至第 个分块,全局最大的scores值,即: 。这两个参数用计算调节系数,如下的scale,对应代码:scores_scale(mi)=exp2f((scores_max_prev(m i)-scores_max_cur)*softmax_scale_log2);。得到调节系数后,更新历史计算的 ,对应代码:row_sum(mi)*=scores_scale ,对应的更新公式如下:
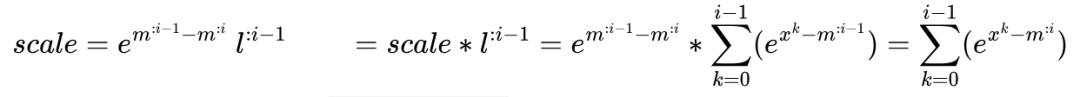
从上面的公式比较容易发现,scores_scale 更新历史 ,将上一个阶段的最大值 消除掉,换成当前阶段的全局最大值。同样的道理 scores_scale 也会更新 tOrO,也就是 。
上文中也提到,FA2是使用的 Q 是外循环, KV 是内循环, FA 3 同样也是这种方式,这里内循环 V 就复用了 t0rO 结果,并不断用 scale 更新 tOrO,得到当前截至当前块的调整值 (从理解公式的角度来看,这里的 可忽略),直到最后一块,那么得到的 就是全局最大值。
上面max更新历史,那么当前的softmax.template online_softmax</*Is_first=*/false, /*Check_inf=*/Is_local>(tSrS);用于计算当前块的local softmax,由于在max函数后面计算,这里用到的为,到目前分块为止(包括当前分块)的最大值。结合online_softmax<false>代码:
template<bool Is_first, bool Check_inf=false, typename Tensor0>
__forceinline__ __device__ TensorT online_softmax(Tensor0 &acc_s) {
...
flash::template scale_apply_exp2</*Scale_max=*/true, Check_inf, Use_max_offset>(scores, row_max, softmax_scale_log2);
flash::reduce_sum</*zero_init=*/false, /*warp_reduce=*/false>(scores, row_sum);
...
};
scale_apply_exp2 计算local softmax(softmax的分子),reduce_sum 将当前的 和历史已经矫正的 相加,对应公式为:
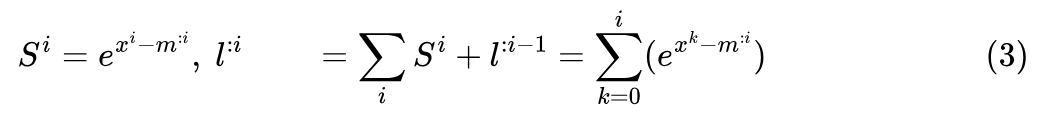
总结整个循环里的逻辑:
-
关键是计算矫正系数 ; -
得到矫正系数后,每次迭代都要更新当前分块 (softmax的分子乘以 的结果),由于 是外循环,对所有的 分块, 都是共享的; -
同样的道理,矫正系数也会矫正历史的 ,然后会跟当前的 累加,需要注意的是 使用到的 是 ,而非 ; -
这样对固定的 分片, 分块迭代完,即可得到最终的softmax的分子和分母( 可以当作系数)。
循环结束后第一个rescale_o作用循环中最后一次的scores_scale, 然后就是cute::copy(softmax.template finalize</*Is_dropout=*/false, Is_split>(tSrS), scores_scale);,其中finalize代码如下:
template<bool Is_dropout=false, bool Split=false, typename Tensor0>
__forceinline__ __device__ TensorT finalize(Tensor0 &acc_s, float descale_v = 1.f, float rp_dropout=1.f) {
constexpr static float max_offset_E = Use_max_offset ? 8.f * float(M_LN2) : 0.f;
// Reshape acc_s from ((2, 2, V), MMA_M, MMA_N) to (nrow=(2, MMA_M), ncol=(2, V, MMA_N))
Tensor scores = make_tensor(acc_s.data(), flash::convert_layout_acc_rowcol(acc_s.layout()));
static_assert(decltype(size<0>(scores))::value == kNRows);
SumOp<float> sum_op;
quad_allreduce_(row_sum, row_sum, sum_op);
TensorT scores_scale;
#pragma unroll
for (int mi = 0; mi < size(row_max); ++mi) {
float sum = row_sum(mi);
float inv_sum = (sum == 0.f || sum != sum) ? 0.f : descale_v / sum;
row_sum(mi) = (sum == 0.f || sum != sum) ? (Split ? -INFINITY : INFINITY) : (row_max(mi) * softmax_scale_log2) * float(M_LN2) - max_offset_E + __logf(sum);
scores_scale(mi) = !Is_dropout ? inv_sum : inv_sum * rp_dropout;
}
return scores_scale;
};
这里主要做的就是将softmax的分子除以分母,细化来说有三个操作:
-
reduce分布在每一个quarter warp中的 ,为啥是 的warp,这个涉及到mma指令输出的数据layout,《FA3的WGMMA数据划分和Mask设计篇》和《理解cutlass的 MMA/WGMMA数据划分篇》都会介绍; -
计算 作用最终的 即为完整的safe softmax公式,这部分跟笔者之前文章中介绍的 FA2的更新公式是完全一致的; -
保存: ,即为 .
Combine_attn_seqk_parallel的公式推导
符号定义
-
lse where ;这里为了方便推导我们将 放到 里面;得到下面结果: -
lse ;
这里需要说明的是: 为啥可以融合到 内,首先需要了解 的作用。 主要防止指数溢出,我们知道Float 32 可以表示的最大数值是 3.4 e 38 ,实际 ,即 在head维度reduce,考虑理想情况下是 (其中 d 是head-size)范围内的均匀分布,那么 结果不会溢出,如果出现异常值, 的结果超过 38 ,那么就会发生精度溢出。减去最大值 为啥可以避免这个问题呢,我们可以通过 的函数曲线来分析这个问题。

从上图不难看出, 在 是发散的,在 是收玫的,所以safe softmax通过将 的结果减去最大值 ,将定义域空间转化到 ,来实现值域不溢出的效果。这项技术在后文中计算LSE值也有应用。还有一个问题是,为什么LSE值可以把 放回去消掉呢。同样可以结合 的函数曲线分析,这里不画图了,直接数值分析,如果想让 正溢出,那么 ,近似得到 ,即 ,这个数值范围足够。同样的道理如果负溢出,那么 的数值也需要到达 。这里有一个近似理解的办法,
显然它的值域空间是他定义域空间的线性函数,这个空间足够使用,不用担心溢出了。
LSE的产生
template<bool Is_dropout=false, bool Split=false, typename Tensor0>
__forceinline__ __device__ TensorT finalize(Tensor0 &acc_s, float descale_v = 1.f, float rp_dropout=1.f) {
constexpr static float max_offset_E = Use_max_offset ? 8.f * float(M_LN2) : 0.f;
// Reshape acc_s from ((2, 2, V), MMA_M, MMA_N) to (nrow=(2, MMA_M), ncol=(2, V, MMA_N))
Tensor scores = make_tensor(acc_s.data(), flash::convert_layout_acc_rowcol(acc_s.layout()));
static_assert(decltype(size<0>(scores))::value == kNRows);
SumOp<float> sum_op;
quad_allreduce_(row_sum, row_sum, sum_op);
TensorT scores_scale;
#pragma unroll
for (int mi = 0; mi < size(row_max); ++mi) {
float sum = row_sum(mi);
float inv_sum = (sum == 0.f || sum != sum) ? 0.f : descale_v / sum;
row_sum(mi) = (sum == 0.f || sum != sum) ? (Split ? -INFINITY : INFINITY) : (row_max(mi) * softmax_scale_log2) * float(M_LN2) - max_offset_E + __logf(sum);
scores_scale(mi) = !Is_dropout ? inv_sum : inv_sum * rp_dropout;
}
return scores_scale;
};
其中的关键语句 row_sum(mi) = (sum == 0.f || sum != sum) ? (Split ? -INFINITY : INFINITY) : (row_max(mi) * softmax_scale_log2) * float(M_LN2) - max_offset_E + __logf(sum);;翻译过来即为(这里忽略max_offset_E): ,合并m即为: 。
求safel
// Compute the logsumexp of the LSE along the split dimension.
ElementAccum lse_max = lse_accum(0);
#pragma unroll
for (int l = 1; l < kNLsePerThread; ++l) { lse_max = max(lse_max, lse_accum(l)); }
MaxOp<float> max_op;
lse_max = Allreduce<kRowsPerLoadTranspose>::run(lse_max, max_op);
lse_max = lse_max == -INFINITY ? 0.0f : lse_max; // In case all local LSEs are -inf
float lse_sum = expf(lse_accum(0) - lse_max);
#pragma unroll
for (int l = 1; l < kNLsePerThread; ++l) { lse_sum += expf(lse_accum(l) - lse_max); }
SumOp<float> sum_op;
lse_sum = Allreduce<kRowsPerLoadTranspose>::run(lse_sum, sum_op);
其中的核心语句是lse_sum += expf(lse_accum(l) - lse_max);
翻译为数学公式得到:

这里减去是为了数值安全,其原理也在上文总结过了。
恢复标准的l
ElementAccum lse_logsum = (lse_sum == 0.f || lse_sum != lse_sum) ? INFINITY : logf(lse_sum) + lse_max;
核心代码:logf(lse_sum) + lse_max,翻译为数学公式:
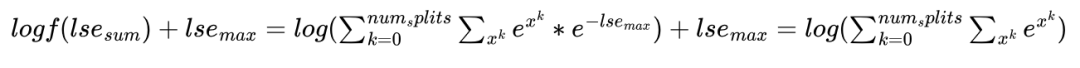
通过消除 ,得到标准的softmax的分母值。这里取 同样是一种保证数值安全的方法,在上文也解释过。最后得到结果是一般形式的softmax的分母取log。
得到最终的softmax矫正系数
#pragma unroll
for (int l = 0; l < kNLsePerThread; ++l) {
const int row = l * kRowsPerLoadTranspose + tidx % kRowsPerLoadTranspose;
const int col = tidx / kRowsPerLoadTranspose;
if (row < params.num_splits && col < kBlockM) { sLSE(row,col) = expf(lse_accum(l) - lse_logsum); }
}
其中的核心代码:expf(lse_accum(l) - lse_logsum);
softmax矫正系数,整个过程依然是数值安全的计算。结合每一分块的输出值:两者相乘并求和即得到最终的结果: 即为最终的结果。
总结
同样是对LSE的应用,splitK的reduce函数相比Ring形式是有差异的,笔者在之前的文章有介绍。造成这个差异的主要原因是Reduce SplitK是在知道所有分块的LSE和output情况,直接可以计算最终的softmax调节系数,而Ring的方式是串行过程,一步步获取下一个分块的LSE和output,并更新,所以有这样的差异。从下一篇开始,就涉及Cutlass的基础知识,所以下一篇会先介绍cutlass。改变计划,下一篇分析FlashMLA。
参考:
https://github.com/Dao-AILab/flash-attention/tree/main/hopper

(文:极市干货)