随着模型规模越来越大，大模型时代的工程能力和 research 能力逐渐变得同等重要。还记得几年前做科研经常看到一些paper改几行matlab、python，就能取得有效的的 performance。不过在当下，我估计很难了。

现如今大模型的训练、复杂的代码嵌套和各种工程挑战，我觉得对曾经做学术的人来说都不是很友好。我自己也深有体会，接触 Megatron-LM 之后，整个人都变得沉静了。

恰好最近看到一个博客，详细地介绍了训练大模型的各种技术。我看完之后，感觉深受启发，因此写一版自己对其的理解与反思，权当记录，也乐得分享，若对读者也能有所帮助，也十分荣幸。

https://jax-ml.github.io/scaling-book/

训练LLM 常常让人感觉像是在搞炼金术，但其实理解和优化模型性能并没有那么神秘。这个 blog 的目标就是帮你揭开扩展语言模型背后的科学原理：TPU（还有 GPU）到底是怎么工作的，它们之间是怎么通信的，LLM 在真实硬件上是如何运行的，以及在训练和推理过程中，如何把模型合理并行化，让它能在大规模场景下高效运行。如果你曾经有过这些疑问：“训练一个 LLM 到底得花多少钱？”“我要自己部署这个模型，需要多大的内存？”“AllGather 到底是啥玩意？”那这些内容，应该会对你有帮助。

当我们在硬件上跑算法时，性能主要受到三个方面的限制：

• • 计算速度 —— 也就是机器做数学运算的能力，比如每秒能处理多少次操作（OPs/second）
• • 带宽 —— 数据在内存、缓存、芯片之间搬运的速度（bytes/second）
• • 总内存容量 —— 也就是设备最多能装下多少数据（bytes）

这些限制就像给计算画出了一条 Roofline：上面顶着计算能力，下面托着内存和带宽瓶颈。通过这套 Roofline 模型，我们可以大致估算出某段计算最快能跑多快（上限）和最慢会卡在哪（下限）。

简单理解一下：如果算法数据太多、内存太小，那它就容易被“撑爆”；如果算法计算量很大但数据搬运太慢，那就等着“搬砖”；如果都不是问题，那就看计算核心有多能打了。这三点加起来，就决定了你模型在硬件上到底能跑多快、扩多大。后面我们会用这个模型来分析怎么高效地扩展模型到更大的硬件，比如 TPUs。

训练模型，哪里需要花时间？

我们运行一个模型，花时间的地方主要有三类：

1. 计算（Computation）

深度学习模型本质上就是一堆矩阵乘法，每个矩阵乘法由大量浮点加法和乘法组成，也就是所谓的 FLOPs（floating point operations）。我们使用的加速卡（GPU 或者 TPU）处理 FLOPs 的速度决定了计算所需要的时间。这里我们定义计算时间  为

举个例子直观理解一下，NVIDIA H100 每秒可以完成大约 9.89e14 个 bfloat16 的 FLOPs，TPU v6e 也差不多是 9.1e14。如果你有一个模型需要做 1e12 个 FLOPs，那在 H100 上大概只需要 1e12 / 9.89e14 = 1.01ms，在 TPU v6e 上大概是 1.1ms。

这告诉我们，只算数学运算的话，其实模型是可以很快的。

2. 芯片内部的通信（Communication within a chip）

模型运行过程中，张量需要在芯片的内存（比如 HBM）和计算核心之间传输。这个传输速度叫 HBM 带宽。对于H100来说，这大约是 3.35TB/s；而对 TPU v6e，大约是 1.6TB/s。

这部分搬数据的时间也需要算进去，特别是当数据量比较大时。

3. 芯片之间的通信（Communication between chips）

当你的模型太大，需要多个加速卡（比如多个 GPU 或 TPU）协作时，张量还需要在不同的芯片之间传来传去。不同的连接方式（比如 ICI, DCN, PCIe）速度不一样，单位和芯片内部通信速度一样，仍然是 bytes/second。到这里，我们也给通信时间  做一个定义：

估算总时间的方式

无论是计算还是通信，我们都可以粗略估计所需时间。并且：

• • 理论下限（Lower bound）：就是计算和通信中耗时更长的那个；
• • 理论上限（Upper bound）：是两者耗时之和。

大多数时候，我们可以通过“通信和计算并行”来让实际耗时更接近下限。因此，优化的目标通常是让通信时间和计算时间尽可能重叠。而即使最坏的情况，也只是差一个因子 2（也就是最长不会慢两倍）。另外，如果计算时间远大于通信时间，那就说明硬件一直在计算、没有等数据，说明我们主要受限于计算能力，处于计算瓶颈（compute-bound）状态；如果反过来是通信时间大于计算时间，那就是我们大部分时间都在“等数据”，说明被通信瓶颈（communication-bound）限制了，FLOPs 的潜力没有完全发挥出来，有浪费。那么我们怎么判断一个操作是计算瓶颈还是通讯瓶颈呢？

算术强度

看一个关键指标：算术强度（Arithmetic Intensity），也叫 Operational Intensity。

注意这里的“通信”既包括芯片内部（如 HBM）也包括芯片之间（如 GPU-GPU）。这个值就表示：“每搬一个字节，能做多少次浮点运算”。直觉上来理解，如果算术强度高：说明每搬一次数据能做很多计算，计算时间就占主导，是计算瓶颈；如果算术强度低，说明大部分时间都在搬数据，计算单元在空转，是通信瓶颈；而这两者“谁主谁次”的拐点，就叫 peak arithmetic intensity（峰值算术强度），也就是：

peak FLOPs/s ÷ 带宽（bytes/s）

峰值算术强度是硬件的一个特性。我们以TPU v5e 为例，它最大计算能力是 1.97e14 FLOPs/s，带宽是 8.2e11 bytes/s，所以它的峰值算术强度大约是1.97e14 / 8.2e11 ≈ 240 FLOPs/byte，这就意味着，如果一个算法的算术强度低于 240，它会变成通信瓶颈。以点积为例，计算两个向量  ，假设它们的长度都是 N，每个元素是 bfloat16：

• • 要从内存读出 x 和 y，每个都是2N 字节，一共 4N 字节（注意：bf16 每个元素是 2 字节，所以这里乘以 2）；
• • 做 N 次乘法，N-1 次加法，共 2N-1 个 FLOPs；
• • 最后再写回 2 字节。

当 N 趋近于无穷大时，整体的算术强度 (2N-1) FLOPs / （4N+2） bytes 近似为 0.5 FLOPs/byte，这个值远远小于 TPU 的 240 FLOPs/byte，所以这个操作是通信瓶颈，说明你即使硬件很强，也没法发挥它的全部计算力。

总结一句话：算术强度就是告诉你：你搬的每一份数据，能不能被“吃干榨净”。如果搬运得多，算得少，硬件再强也浪费；如果算得多，搬得少，那你就能用满算力。这就是判断计算 vs 通信瓶颈的核心标准。

Roofline

我们可以用一种叫做 Roofline 图的方式，把计算能力和内存带宽的权衡形象地画出来。这个图是个对数坐标图，横轴是算术强度（FLOPs per byte），纵轴是你在特定硬件上能达到的最大吞吐量（FLOPs/s）。

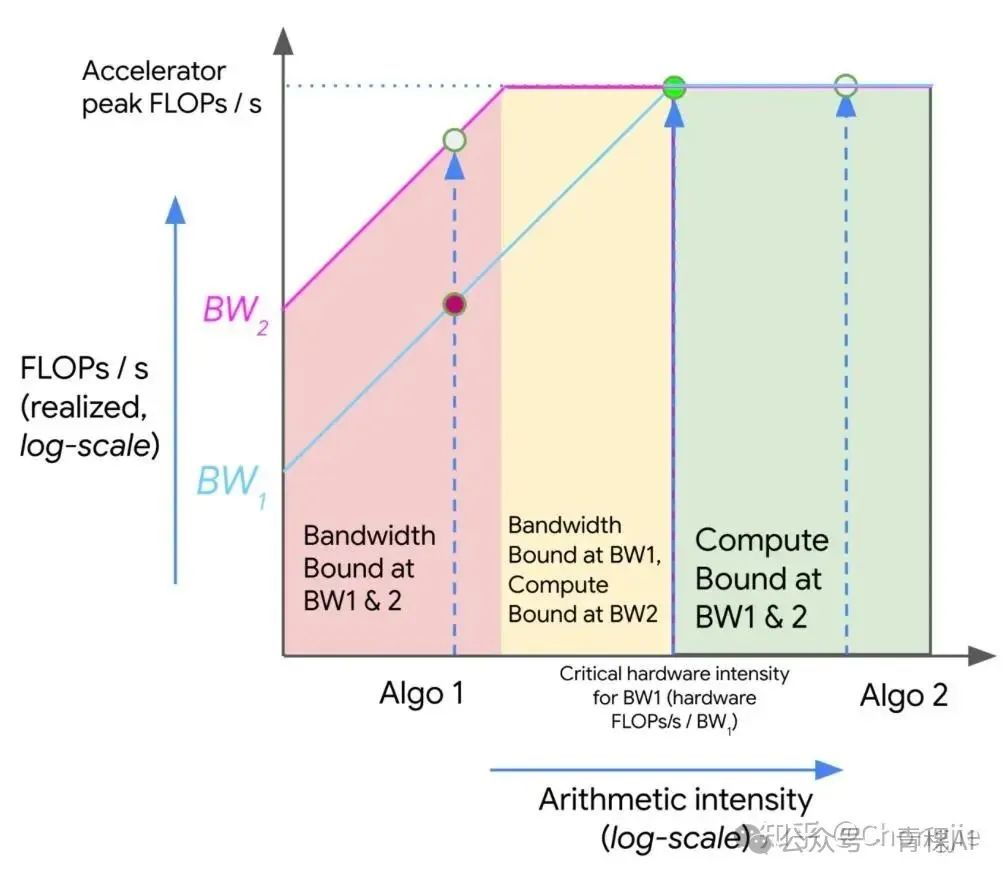
图上会看到几条线：

• • 红色区域：算法的算术强度太低，无论你的带宽是 BW1 还是 BW2，都会被带宽限制住，硬件的 FLOPs 没有被用满。
• • 黄色区域：算法在低带宽（BW1）下受限，但如果你换个高带宽（BW2）就能跑快。
• • 绿色区域：算术强度足够高，不再受内存带宽影响，这时瓶颈变成了计算能力，硬件跑满了

图中也有两个算法：

• • Algo 1（左边）：算术强度低，受限于内存带宽，只用到了硬件一小部分计算力，是通信瓶颈。
• • Algo 2（右边）：算术强度高，达到了硬件的峰值 FLOPs/s，是计算瓶颈，充分利用了硬件。

这张图告诉我们：如果一个算法在红区，你可以通过提高算术强度（比如增加计算量、减少内存访问）或者提高内存带宽来让它更快；如果一个算法已经在绿区，那再提带宽或者强度没啥意义了，因为已经计算瓶颈了。

矩阵乘法

讲了这么多，我们来看一个实际的应用。我们考虑最常见的算法之一：矩阵乘法（matrix multiplication，简称 matmul）。

假设你有两个矩阵：X，大小 bf16[B, D]，Y，大小 bf16[D, F]，得到结果矩阵 Z bf16[B, F]。为了计算这个 matmul，你得从内存里读取 2DF + 2BD 字节的数据，执行 2BDF 个 FLOPs（每次乘法+加法）；然后把 Z 写回内存，要写 2BF 字节。

如果我们假设 B（batch size）远小于 D 和 F，也就是 token 数相对 embedding size 和头数小得多（这在 Transformer 中很常见），那么算术强度大约就是：

换句话说，这个强度跟 batch size 成正比。所以，在 TPU v5e 上，如果你用的是 bfloat16 类型，那么只要你的 batch size 超过 240 个 token，你就可以做到 compute-bound。

当然，这些都是单卡内的 memory-bandwidth 限制，也就是看显存带宽能不能喂饱计算。但这其实只是最简单的一类 roofline，现实中我们更常遇到的瓶颈是多卡之间的通信带宽，尤其是在多个 TPU/GPU 上做分布式矩阵乘法时。来举个例子，还是原来的 X 和 Y，你把它们在维度 D 上一分为二，分别放在两张卡（比如 2 个 TPU）。现在你要做矩阵乘法，做法如下：

• • 在 TPU 0 上：算前一半： A = X[:, :D//2] @ Y[:D//2, :]
• • 在 TPU 1 上：算后一半： B = X[:, D//2:] @ Y[D//2:, :]
• • 然后两张卡交换 A 和 B 的结果，把它们加起来得到最终输出。

对于这一次，每张卡只做一半的工作，所以计算时间是原来的一半：

而通信时间是两个卡交换结果的时间，也就是：

我们要找出什么时候通信时间小于计算时间（也就是还能跑满卡，不受通信限制），解这个不等式：

也就是说：只要你的 embedding size D > 8755，通信就不是瓶颈，你是 compute-bound；反之就是 communication-bound。在这个场景下，决定是否 compute-bound 的，不是 batch size B，而是特征维度 D。

多卡分布式计算下的 roofline 限制关键在于通信带宽，是否能充分利用硬件取决于通信 vs. 计算的比例 —— 而这个比例依赖于模型维度，不是 batch size。理解这个规律，才能知道你什么时候该切分模型、怎么切分才能不踩通信瓶颈。