博客来源:https://leimao.github.io/article/CUDA-Matrix-Multiplication-Optimization/ ,来自Lei Mao,已获得作者转载授权。后续会转载一些Lei Mao的CUDA相关Blog,也是一个完整的专栏,Blog会从稍早一些的CUDA架构到当前最新的CUDA架构,也会包含实用工程技巧,底层指令分析,Cutlass分析等等多个课题,是一个时间线十分明确的专栏。
CUDA 矩阵乘法优化
介绍
通用矩阵乘法(GEMM)是线性代数中的基本运算。它也是许多科学计算应用中非常重要的运算,如机器学习和深度学习。
在本文中,我们将讨论如何使用 CUDA 优化 NVIDIA GPU 上 FP32 GEMM 的性能,以及如何使用 NVIDIA Tensor Core 将 FP32 GEMM 优化扩展到 FP16 GEMM。
通用矩阵乘法
GEMM 运算计算 ,其中 ,,,。在计算机程序中,通常 和 是常量输入矩阵, 将被输出矩阵 覆盖。
在我们的实现中,我们假设所有矩阵 、、 和 都以行主序存储在内存中,对于 FP32 矩阵,主维度填充为 64 字节,对于 FP16 矩阵,主维度填充为 32 字节。
具有非合并内存访问的朴素实现
朴素实现是使用 2D 块,其中每个线程负责计算输出矩阵的一个元素。具体来说,对于全局线程索引为 的每个线程,其中 和 ,它计算
以下代码片段显示了朴素实现。
template <typename T>
__global__ void gemm_v00(size_t m, size_t n, size_t k, T alpha, T const* A,
size_t lda, T const* B, size_t ldb, T beta, T* C,
size_t ldc)
{
// Compute the row and column of C that this thread is responsible for.
size_tconst C_row_idx{blockIdx.x * blockDim.x + threadIdx.x};
size_tconst C_col_idx{blockIdx.y * blockDim.y + threadIdx.y};
// Each thread compute
// C[C_row_idx, C_col_idx] = alpha * A[C_row_idx, :] * B[:, C_col_idx] +
// beta * C[C_row_idx, C_col_idx].
if (C_row_idx < m && C_col_idx < n)
{
T sum{static_cast<T>(0)};
for (size_t k_idx{0U}; k_idx < k; ++k_idx)
{
sum += A[C_row_idx * lda + k_idx] * B[k_idx * ldb + C_col_idx];
}
C[C_row_idx * ldc + C_col_idx] =
alpha * sum + beta * C[C_row_idx * ldc + C_col_idx];
}
}
template <typename T>
void launch_gemm_kernel_v00(size_t m, size_t n, size_t k, T const* alpha,
T const* A, size_t lda, T const* B, size_t ldb,
T const* beta, T* C, size_t ldc,
cudaStream_t stream)
{
dim3 const block_dim{32U, 32U, 1U};
dim3 const grid_dim{
(static_cast<unsignedint>(m) + block_dim.x - 1U) / block_dim.x,
(static_cast<unsignedint>(n) + block_dim.y - 1U) / block_dim.y, 1U};
gemm_v00<T><<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B,
ldb, *beta, C, ldc);
CHECK_LAST_CUDA_ERROR();
}
然而,除了朴素算法的其他缺点之外,这个实现还有一个主要问题,即读取和写入全局内存时的非合并内存访问。在我们的实现中,由于疏忽使用快速线程索引来索引矩阵 和 的行,同一 warp 中的线程从以行主序存储在内存中的矩阵 的同一列读取元素,由于读取完全不连续,导致非合并内存访问。当 warp 覆写矩阵 的元素时也会发生同样的问题。同一 warp 中的线程读取矩阵 的同一元素,导致广播内存访问,这不受疏忽的影响。
这个 FP32 GEMM 实现的性能在 NVIDIA GeForce RTX 3090 GPU 上仅为 0.27 TFLOPS,性能非常差。
具有合并内存访问的朴素实现
解决非合并内存访问的方法是使用快速线程索引来索引以行主序存储在内存中的矩阵的行,这样同一 warp 中的线程读取或覆写矩阵同一行的元素时是合并的。在我们的实现中,我们只需要在内核函数中交换快速线程索引和慢速线程索引。
以下代码片段显示了具有合并内存访问的朴素实现。
template <typename T>
__global__ void gemm_v01(size_t m, size_t n, size_t k, T alpha, T const* A,
size_t lda, T const* B, size_t ldb, T beta, T* C,
size_t ldc)
{
// Compute the row and column of C that this thread is responsible for.
size_tconst C_col_idx{blockIdx.x * blockDim.x + threadIdx.x};
size_tconst C_row_idx{blockIdx.y * blockDim.y + threadIdx.y};
// Each thread compute
// C[C_row_idx, C_col_idx] = alpha * A[C_row_idx, :] * B[:, C_col_idx] +
// beta * C[C_row_idx, C_col_idx].
if (C_row_idx < m && C_col_idx < n)
{
T sum{static_cast<T>(0)};
for (size_t k_idx{0U}; k_idx < k; ++k_idx)
{
sum += A[C_row_idx * lda + k_idx] * B[k_idx * ldb + C_col_idx];
}
C[C_row_idx * ldc + C_col_idx] =
alpha * sum + beta * C[C_row_idx * ldc + C_col_idx];
}
}
template <typename T>
void launch_gemm_kernel_v01(size_t m, size_t n, size_t k, T const* alpha,
T const* A, size_t lda, T const* B, size_t ldb,
T const* beta, T* C, size_t ldc,
cudaStream_t stream)
{
dim3 const block_dim{32U, 32U, 1U};
dim3 const grid_dim{
(static_cast<unsignedint>(n) + block_dim.x - 1U) / block_dim.x,
(static_cast<unsignedint>(m) + block_dim.y - 1U) / block_dim.y, 1U};
gemm_v01<T><<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B,
ldb, *beta, C, ldc);
CHECK_LAST_CUDA_ERROR();
}
现在,由于这个修复,同一warp中的线程从以行主序存储在内存中的矩阵的同一行读取元素,导致合并内存访问。当warp覆写矩阵的元素时也会发生同样的情况。同一warp中的线程读取矩阵的同一元素,导致广播内存访问。因此,这个实现应该比非合并内存访问的实现性能好得多。
这个FP32 GEMM实现的性能在NVIDIA GeForce RTX 3090 GPU上变成了1.72 TFLOPS,比之前的实现好得多。然而,考虑到GPU的理论峰值性能是35.58 TFLOPS,这个实现的性能仍然很差。
具有2D块分块的实现
由于前面的实现频繁访问全局内存,GEMM实现变成了内存受限的。由于访问共享内存比访问全局内存快得多,为了提高性能,我们可以使用共享内存来缓存输入矩阵和以实现数据重用。
然而,由于共享内存大小有限,我们无法在共享内存中缓存整个输入矩阵和。相反,我们可以在共享内存中缓存和的2D分块,并使用2D分块来计算输出矩阵的2D分块。然后,我们可以将和的下一个2D分块加载到共享内存中,并计算的下一个2D分块。
数学上,给定一个GEMM运算,其中,,,,矩阵可以被分成更小的矩阵。
每个中的小矩阵都是通过多个小矩阵乘法和累加计算的。
在这个实现中,每个具有块索引的2D块,其中和,负责计算一个小矩阵。共享内存用于缓存大小分别为和的和的2D分块。的2D分块由索引,其中和。的2D分块由索引,其中和。缓存和小矩阵乘法计算过程重复次,直到整个小矩阵被累加完成。
与之前的实现类似,每个块需要个线程来计算小矩阵,每个具有块线程索引的线程,其中和,负责计算小矩阵的一个元素。
下面的代码片段展示了使用2D块分块的实现。
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
size_t BLOCK_TILE_SIZE_K, size_t NUM_THREADS, size_t BLOCK_TILE_SKEW_SIZE_X = 0U, size_t BLOCK_TILE_SKEW_SIZE_K = 0U>
__device__ void load_data_to_shared_memory(T const* A, size_t lda,
T const* B, size_t ldb,
T A_thread_block_tile[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_K + BLOCK_TILE_SKEW_SIZE_K],
T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X + BLOCK_TILE_SKEW_SIZE_X],
size_t thread_block_tile_idx,
size_t thread_linear_idx,
size_t m, size_t n,
size_t k)
{
// 将DRAM中的矩阵A数据加载到共享内存中的A_thread_block_tile
#pragma unroll
for (size_t load_idx{0U};
load_idx <
(BLOCK_TILE_SIZE_Y * BLOCK_TILE_SIZE_K + NUM_THREADS - 1U) /
NUM_THREADS;
++load_idx)
{
// 计算在共享内存分块中的行列索引
size_tconst A_thread_block_tile_row_idx{
(thread_linear_idx + load_idx * NUM_THREADS) /
BLOCK_TILE_SIZE_K};
size_tconst A_thread_block_tile_col_idx{
(thread_linear_idx + load_idx * NUM_THREADS) %
BLOCK_TILE_SIZE_K};
// 计算在全局矩阵A中的行列索引
size_tconst A_row_idx{blockIdx.y * BLOCK_TILE_SIZE_Y +
A_thread_block_tile_row_idx};
size_tconst A_col_idx{thread_block_tile_idx * BLOCK_TILE_SIZE_K +
A_thread_block_tile_col_idx};
// 边界检查可能会在一定程度上降低内核性能
// 但是能够保证内核对所有不同GEMM配置的正确性
T val{static_cast<T>(0)};
if (A_row_idx < m && A_col_idx < k)
{
val = A[A_row_idx * lda + A_col_idx];
}
// 这个if语句会降低内核性能
// 在主机代码中添加静态断言来保证这个if条件总是为true
static_assert(BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_Y % NUM_THREADS ==
0U);
// if (A_thread_block_tile_row_idx < BLOCK_TILE_SIZE_Y &&
// A_thread_block_tile_col_idx < BLOCK_TILE_SIZE_K)
// {
// A_thread_block_tile[A_thread_block_tile_row_idx]
// [A_thread_block_tile_col_idx] = val;
// }
A_thread_block_tile[A_thread_block_tile_row_idx]
[A_thread_block_tile_col_idx] = val;
}
// 将DRAM中的矩阵B数据加载到共享内存中的B_thread_block_tile
#pragma unroll
for (size_t load_idx{0U};
load_idx <
(BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_X + NUM_THREADS - 1U) /
NUM_THREADS;
++load_idx)
{
// 计算在共享内存分块中的行列索引
size_tconst B_thread_block_tile_row_idx{
(thread_linear_idx + load_idx * NUM_THREADS) /
BLOCK_TILE_SIZE_X};
size_tconst B_thread_block_tile_col_idx{
(thread_linear_idx + load_idx * NUM_THREADS) %
BLOCK_TILE_SIZE_X};
// 计算在全局矩阵B中的行列索引
size_tconst B_row_idx{thread_block_tile_idx * BLOCK_TILE_SIZE_K +
B_thread_block_tile_row_idx};
size_tconst B_col_idx{blockIdx.x * BLOCK_TILE_SIZE_X +
B_thread_block_tile_col_idx};
// 边界检查可能会在一定程度上降低内核性能
// 但是能够保证内核对所有不同GEMM配置的正确性
T val{static_cast<T>(0)};
if (B_row_idx < k && B_col_idx < n)
{
val = B[B_row_idx * ldb + B_col_idx];
}
// 这个if语句会降低内核性能
// 在主机代码中添加静态断言来保证这个if条件总是为true
static_assert(BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_K % NUM_THREADS ==
0U);
// if (B_thread_block_tile_row_idx < BLOCK_TILE_SIZE_K &&
// B_thread_block_tile_col_idx < BLOCK_TILE_SIZE_X)
// {
// B_thread_block_tile[B_thread_block_tile_row_idx]
// [B_thread_block_tile_col_idx] = val;
// }
B_thread_block_tile[B_thread_block_tile_row_idx]
[B_thread_block_tile_col_idx] = val;
}
}
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
size_t BLOCK_TILE_SIZE_K>
__global__ void gemm_v02(size_t m, size_t n, size_t k, T alpha, T const* A,
size_t lda, T const* B, size_t ldb, T beta, T* C,
size_t ldc)
{
// 避免使用blockDim.x * blockDim.y作为每个块的线程数
// 因为它是一个运行时常数,编译器无法基于它优化循环展开
// 改为使用编译时常数
constexprsize_t NUM_THREADS{BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y};
size_tconst thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};
// 计算此线程负责的矩阵C的行列索引
size_tconst C_col_idx{blockIdx.x * blockDim.x + threadIdx.x};
size_tconst C_row_idx{blockIdx.y * blockDim.y + threadIdx.y};
// 在共享内存中缓存A和B的分块以实现数据重用
__shared__ T A_thread_block_tile[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_K];
__shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X];
// 计算需要处理的线程块分块数量
size_tconst num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
BLOCK_TILE_SIZE_K};
// 累加和初始化为0
T sum{static_cast<T>(0)};
// 遍历每个线程块分块
for (size_t thread_block_tile_idx{0U};
thread_block_tile_idx < num_thread_block_tiles;
++thread_block_tile_idx)
{
// 加载当前分块的数据到共享内存
load_data_to_shared_memory<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
BLOCK_TILE_SIZE_K, NUM_THREADS>(
A, lda, B, ldb, A_thread_block_tile, B_thread_block_tile,
thread_block_tile_idx, thread_linear_idx, m, n, k);
__syncthreads();
// 计算当前分块的矩阵乘法
#pragma unroll
for (size_t k_i{0U}; k_i < BLOCK_TILE_SIZE_K; ++k_i)
{
// 这样做会导致性能达到2 TOPS
// 假设blockDim.x = blockDim.y = 32
// 实际上,对于一个warp,在一次迭代中,我们从A_thread_block_tile的
// 共享内存同一位置读取值,导致广播,我们也从B_thread_block_tile
// 读取32个没有bank冲突的值。即使如此,所有值都必须从共享内存读取,
// 结果是共享内存指令运行得非常密集,只是为了使用简单的算术指令
// 计算少量值,这是不高效的
sum += A_thread_block_tile[threadIdx.y][k_i] *
B_thread_block_tile[k_i][threadIdx.x];
}
__syncthreads();
}
// 将最终结果写入输出矩阵C(边界检查)
if (C_row_idx < m && C_col_idx < n)
{
C[C_row_idx * ldc + C_col_idx] =
alpha * sum + beta * C[C_row_idx * ldc + C_col_idx];
}
}
template <typename T>
void launch_gemm_kernel_v02(size_t m, size_t n, size_t k, T const* alpha,
T const* A, size_t lda, T const* B, size_t ldb,
T const* beta, T* C, size_t ldc,
cudaStream_t stream)
{
// 可以随意调整块分块大小
// 算法正确性应该始终得到保证
constexprunsignedint BLOCK_TILE_SIZE_X{32U};
constexprunsignedint BLOCK_TILE_SIZE_Y{32U};
constexprunsignedint BLOCK_TILE_SIZE_K{32U};
constexprunsignedint NUM_THREADS{BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y};
// 静态断言确保分块大小与线程数兼容
static_assert(BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_Y % NUM_THREADS == 0U);
static_assert(BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_K % NUM_THREADS == 0U);
// 设置块维度
dim3 const block_dim{BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, 1U};
// 设置网格维度
dim3 const grid_dim{
(static_cast<unsignedint>(n) + block_dim.x - 1U) / block_dim.x,
(static_cast<unsignedint>(m) + block_dim.y - 1U) / block_dim.y, 1U};
// 启动GEMM内核
gemm_v02<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K>
<<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B, ldb,
*beta, C, ldc);
CHECK_LAST_CUDA_ERROR();
}
这个FP32 GEMM实现的性能在NVIDIA GeForce RTX 3090 GPU上变成了2.66 TFLOPS,比之前的实现好得多。然而,它仍然远远低于GPU的理论峰值性能。
这个实现的问题是共享内存被频繁访问。即使访问共享内存比访问全局内存快得多,共享内存指令运行得非常密集,只是为了使用简单的算术指令计算少量值,这是不高效的。因此,这个实现的性能仍然受限于内存带宽,这次来自共享内存。
具有2D块分块和1D线程分块的实现
为了进一步提高性能,我们可以通过进一步缓存输入矩阵和的更小的分块到线程的寄存器中来缓解共享内存带宽问题。这次,每个线程负责计算输出矩阵的一个小分块,而不是一个单个元素。因为寄存器是最快的访问方式,这个实现的性能应该比之前的实现好得多。
我们首先只缓存矩阵的数据从共享内存到寄存器。每个具有块线程索引的线程,其中和,现在负责计算小矩阵的个元素,其中是线程分块大小。
在我们之前的实现中没有线程分块,为了计算小矩阵的一个元素,我们需要从共享内存中缓存的矩阵中读取个值,从共享内存中缓存的矩阵中读取个值。总共需要从共享内存中读取个值。
现在,有了1D线程分块,为了计算小矩阵的个元素,我们只需要从共享内存中缓存的矩阵中读取个值,从共享内存中缓存的矩阵中读取个值。具体来说,在每个内层循环中,被缓存到寄存器中以被重复使用次。总共需要从共享内存中读取个值。平均来说,为了计算小矩阵的一个元素,我们需要从共享内存中读取个值。
因为 ,共享内存访问频率降低,共享内存带宽问题得到缓解。
下面的代码片段展示了使用2D块分块和1D线程分块的实现。
// 使用2D块分块和1D线程分块的GEMM内核模板
// T: 数据类型
// BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K: 块分块大小
// THREAD_TILE_SIZE_Y: 线程分块大小(每个线程处理的行数)
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
size_t BLOCK_TILE_SIZE_K, size_t THREAD_TILE_SIZE_Y>
__global__ void gemm_v03(size_t m, size_t n, size_t k, T alpha, T const* A,
size_t lda, T const* B, size_t ldb, T beta, T* C,
size_t ldc)
{
// 避免使用blockDim.x * blockDim.y作为每个块的线程数
// 因为它是运行时常量,编译器无法基于此优化循环展开
// 使用编译时常量代替
constexprsize_t NUM_THREADS{BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y /
THREAD_TILE_SIZE_Y};
// 计算线程的线性索引
size_tconst thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};
// 在共享内存中缓存A和B的分块以实现数据重用
__shared__ T A_thread_block_tile[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_K];
__shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X];
// 计算需要处理的线程块分块数量
size_tconst num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
BLOCK_TILE_SIZE_K};
// 块中的每个线程处理THREAD_TILE_SIZE_Y个输出值
// 具体来说,这些值对应于
// C[blockIdx.y * BLOCK_TILE_SIZE_Y + threadIdx.x / BLOCK_TILE_SIZE_X *
// THREAD_TILE_SIZE_Y : blockIdx.y * BLOCK_TILE_SIZE_Y + (threadIdx.x /
// BLOCK_TILE_SIZE_X + 1) * THREAD_TILE_SIZE_Y][blockIdx.x *
// BLOCK_TILE_SIZE_X + threadIdx.x % BLOCK_TILE_SIZE_X]
T C_thread_results[THREAD_TILE_SIZE_Y] = {static_cast<T>(0)};
// 遍历所有线程块分块
for (size_t thread_block_tile_idx{0U};
thread_block_tile_idx < num_thread_block_tiles;
++thread_block_tile_idx)
{
// 将数据从全局内存加载到共享内存
load_data_to_shared_memory<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
BLOCK_TILE_SIZE_K, NUM_THREADS>(
A, lda, B, ldb, A_thread_block_tile, B_thread_block_tile,
thread_block_tile_idx, thread_linear_idx, m, n, k);
// 同步所有线程,确保共享内存数据加载完成
__syncthreads();
// 遍历K维度进行矩阵乘法计算
#pragma unroll
for (size_t k_i{0U}; k_i < BLOCK_TILE_SIZE_K; ++k_i)
{
size_tconst B_thread_block_tile_row_idx{k_i};
// B_val被缓存在寄存器中以减轻共享内存访问压力
T const B_val{
B_thread_block_tile[B_thread_block_tile_row_idx]
[thread_linear_idx % BLOCK_TILE_SIZE_X]};
// 遍历线程分块的每一行
#pragma unroll
for (size_t thread_tile_row_idx{0U};
thread_tile_row_idx < THREAD_TILE_SIZE_Y;
++thread_tile_row_idx)
{
// 计算A矩阵在共享内存中的行索引
size_tconst A_thread_block_tile_row_idx{
thread_linear_idx / BLOCK_TILE_SIZE_X * THREAD_TILE_SIZE_Y +
thread_tile_row_idx};
// 计算A矩阵在共享内存中的列索引
size_tconst A_thread_block_tile_col_idx{k_i};
// 从共享内存中读取A矩阵的值
T const A_val{A_thread_block_tile[A_thread_block_tile_row_idx]
[A_thread_block_tile_col_idx]};
// 执行乘累加操作
C_thread_results[thread_tile_row_idx] += A_val * B_val;
}
}
// 同步所有线程,准备下一次迭代
__syncthreads();
}
// 将结果写入DRAM
#pragma unroll
for (size_t thread_tile_row_idx{0U};
thread_tile_row_idx < THREAD_TILE_SIZE_Y; ++thread_tile_row_idx)
{
// 计算输出矩阵C的行索引
size_tconst C_row_idx{blockIdx.y * BLOCK_TILE_SIZE_Y +
thread_linear_idx / BLOCK_TILE_SIZE_X *
THREAD_TILE_SIZE_Y +
thread_tile_row_idx};
// 计算输出矩阵C的列索引
size_tconst C_col_idx{blockIdx.x * BLOCK_TILE_SIZE_X +
thread_linear_idx % BLOCK_TILE_SIZE_X};
// 边界检查并写入结果
if (C_row_idx < m && C_col_idx < n)
{
C[C_row_idx * ldc + C_col_idx] =
alpha * C_thread_results[thread_tile_row_idx] +
beta * C[C_row_idx * ldc + C_col_idx];
}
}
}
// 启动GEMM内核v03的模板函数
template <typename T>
void launch_gemm_kernel_v03(size_t m, size_t n, size_t k, T const* alpha,
T const* A, size_t lda, T const* B, size_t ldb,
T const* beta, T* C, size_t ldc,
cudaStream_t stream)
{
// 可以随意调整块分块大小
// 算法正确性应该始终得到保证
constexprunsignedint BLOCK_TILE_SIZE_X{64U}; // 块分块X维度大小
constexprunsignedint BLOCK_TILE_SIZE_Y{64U}; // 块分块Y维度大小
constexprunsignedint BLOCK_TILE_SIZE_K{8U}; // 块分块K维度大小
// 每个线程计算C矩阵的THREAD_TILE_SIZE_Y个值
constexprunsignedint THREAD_TILE_SIZE_Y{8U}; // 线程分块大小
// 计算每个块的线程数
constexprunsignedint NUM_THREADS_PER_BLOCK{
BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y / THREAD_TILE_SIZE_Y};
// 静态断言确保参数配置的正确性
static_assert(BLOCK_TILE_SIZE_Y % THREAD_TILE_SIZE_Y == 0U);
static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_K == 0U);
static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_X == 0U);
// 设置块维度(一维线程块)
dim3 const block_dim{NUM_THREADS_PER_BLOCK, 1U, 1U};
// 设置网格维度
dim3 const grid_dim{
(static_cast<unsignedint>(n) + BLOCK_TILE_SIZE_X - 1U) /
BLOCK_TILE_SIZE_X,
(static_cast<unsignedint>(m) + BLOCK_TILE_SIZE_Y - 1U) /
BLOCK_TILE_SIZE_Y,
1U};
// 启动GEMM内核
gemm_v03<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K,
THREAD_TILE_SIZE_Y><<<grid_dim, block_dim, 0U, stream>>>(
m, n, k, *alpha, A, lda, B, ldb, *beta, C, ldc);
// 检查CUDA错误
CHECK_LAST_CUDA_ERROR();
}
这个FP32 GEMM实现的性能在NVIDIA GeForce RTX 3090 GPU上变成了8.91 TFLOPS。看起来我们一直在取得进展。
具有2D块分块和2D线程分块的实现
如果寄存器数量不是性能瓶颈,我们可以通过缓存矩阵和的数据从共享内存到寄存器来进一步提高性能。每个具有块线程索引的线程,其中和,现在负责计算小矩阵的个元素,其中和分别是行和列的线程分块大小。
在我们之前的实现中有了1D线程分块,为了计算小矩阵的一个元素,我们平均需要从共享内存中读取个值。
现在,有了2D线程分块,为了计算小矩阵的个元素,我们只需要从共享内存中读取个值。具体来说,在每个内层循环中,和被缓存到寄存器中以被重复使用来计算矩阵乘法。总共需要从共享内存中读取个值。平均来说,为了计算小矩阵的一个元素,我们需要从共享内存中读取个值。
因为 ,共享内存访问频率进一步降低,共享内存带宽问题得到进一步缓解。
下面是另一种描述2D线程分块实现的方法。
数学上,给定一个矩阵乘法和累加操作 ,其中 ,,,,矩阵可以被分成更小的矩阵。
中的每个小矩阵都是通过多个小矩阵乘法和累加计算的。
综合起来,线程分块 可以按如下方式计算。
在此实现中,我们设置 以使线程分块算法更简单。
以下代码片段展示了使用2D块分块和2D线程分块的实现。
// GEMM内核v04版本
// 从全局内存进行合并读写访问
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
size_t BLOCK_TILE_SIZE_K, size_t THREAD_TILE_SIZE_X,
size_t THREAD_TILE_SIZE_Y>
__global__ void gemm_v04(size_t m, size_t n, size_t k, T alpha, T const* A,
size_t lda, T const* B, size_t ldb, T beta, T* C,
size_t ldc)
{
// 避免使用blockDim.x * blockDim.y作为每个块的线程数
// 因为它是运行时常量,编译器无法基于此优化循环展开
// 使用编译时常量代替
constexprsize_t NUM_THREADS{BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y /
(THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y)};
// 计算线程的线性索引
size_tconst thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};
// 在共享内存中缓存A和B的分块以实现数据重用
__shared__ T A_thread_block_tile[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_K];
__shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X];
// 计算需要处理的线程块分块数量
size_tconst num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
BLOCK_TILE_SIZE_K};
// 块中的每个线程处理THREAD_TILE_SIZE_Y * THREAD_TILE_SIZE_X个输出值
// 具体来说,这些值对应于输出矩阵C中的一个小矩形区域
// C[blockIdx.y * BLOCK_TILE_SIZE_Y + threadIdx.x / BLOCK_TILE_SIZE_X *
// THREAD_TILE_SIZE_Y : blockIdx.y * BLOCK_TILE_SIZE_Y + (threadIdx.x /
// BLOCK_TILE_SIZE_X + 1) * THREAD_TILE_SIZE_Y][blockIdx.x *
// BLOCK_TILE_SIZE_X + threadIdx.x % BLOCK_TILE_SIZE_X *
// THREAD_TILE_SIZE_X : blockIdx.x * BLOCK_TILE_SIZE_X + (threadIdx.x %
// BLOCK_TILE_SIZE_X + 1) * THREAD_TILE_SIZE_X]
T C_thread_results[THREAD_TILE_SIZE_Y][THREAD_TILE_SIZE_X] = {
static_cast<T>(0)};
// A_vals缓存在寄存器中,存储当前线程分块的A矩阵值
T A_vals[THREAD_TILE_SIZE_Y] = {static_cast<T>(0)};
// B_vals缓存在寄存器中,存储当前线程分块的B矩阵值
T B_vals[THREAD_TILE_SIZE_X] = {static_cast<T>(0)};
// 遍历所有的线程块分块
for (size_t thread_block_tile_idx{0U};
thread_block_tile_idx < num_thread_block_tiles;
++thread_block_tile_idx)
{
// 将数据从全局内存加载到共享内存
load_data_to_shared_memory<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
BLOCK_TILE_SIZE_K, NUM_THREADS>(
A, lda, B, ldb, A_thread_block_tile, B_thread_block_tile,
thread_block_tile_idx, thread_linear_idx, m, n, k);
__syncthreads();
// 对当前分块进行矩阵乘法计算
#pragma unroll
for (size_t k_i{0U}; k_i < BLOCK_TILE_SIZE_K; ++k_i)
{
// 计算当前线程在A分块中的行索引
size_tconst A_thread_block_tile_row_idx{
thread_linear_idx / (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
THREAD_TILE_SIZE_Y};
// 计算当前线程在A分块中的列索引
size_tconst A_thread_block_tile_col_idx{k_i};
// 从共享内存中加载A矩阵的值到寄存器
#pragma unroll
for (size_t thread_tile_row_idx{0U};
thread_tile_row_idx < THREAD_TILE_SIZE_Y;
++thread_tile_row_idx)
{
// 访问A_thread_block_tile的值时会有共享内存bank冲突
// 我们可以通过在从DRAM加载数据时转置A_thread_block_tile来改善这一点
A_vals[thread_tile_row_idx] =
A_thread_block_tile[A_thread_block_tile_row_idx +
thread_tile_row_idx]
[A_thread_block_tile_col_idx];
}
// 计算当前线程在B分块中的行索引
size_tconst B_thread_block_tile_row_idx{k_i};
// 计算当前线程在B分块中的列索引
size_tconst B_thread_block_tile_col_idx{
thread_linear_idx % (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
THREAD_TILE_SIZE_X};
// 从共享内存中加载B矩阵的值到寄存器
#pragma unroll
for (size_t thread_tile_col_idx{0U};
thread_tile_col_idx < THREAD_TILE_SIZE_X;
++thread_tile_col_idx)
{
B_vals[thread_tile_col_idx] =
B_thread_block_tile[B_thread_block_tile_row_idx]
[B_thread_block_tile_col_idx +
thread_tile_col_idx];
}
// 执行线程分块的矩阵乘法计算
for (size_t thread_tile_row_idx{0U};
thread_tile_row_idx < THREAD_TILE_SIZE_Y;
++thread_tile_row_idx)
{
for (size_t thread_tile_col_idx{0U};
thread_tile_col_idx < THREAD_TILE_SIZE_X;
++thread_tile_col_idx)
{
// 累加计算结果:C += A * B
C_thread_results[thread_tile_row_idx]
[thread_tile_col_idx] +=
A_vals[thread_tile_row_idx] *
B_vals[thread_tile_col_idx];
}
}
}
__syncthreads();
}
// 将计算结果写入全局内存(DRAM)
for (size_t thread_tile_row_idx{0U};
thread_tile_row_idx < THREAD_TILE_SIZE_Y; ++thread_tile_row_idx)
{
for (size_t thread_tile_col_idx{0U};
thread_tile_col_idx < THREAD_TILE_SIZE_X; ++thread_tile_col_idx)
{
// 计算输出矩阵C中的行索引
size_tconst C_row_idx{
blockIdx.y * BLOCK_TILE_SIZE_Y +
threadIdx.x / (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
THREAD_TILE_SIZE_Y +
thread_tile_row_idx};
// 计算输出矩阵C中的列索引
size_tconst C_col_idx{
blockIdx.x * BLOCK_TILE_SIZE_X +
threadIdx.x % (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
THREAD_TILE_SIZE_X +
thread_tile_col_idx};
// 边界检查,确保不越界
if (C_row_idx < m && C_col_idx < n)
{
// 执行GEMM操作:C = alpha * A * B + beta * C
C[C_row_idx * ldc + C_col_idx] =
alpha * C_thread_results[thread_tile_row_idx]
[thread_tile_col_idx] +
beta * C[C_row_idx * ldc + C_col_idx];
}
}
}
}
// GEMM内核v04的启动函数
template <typename T>
void launch_gemm_kernel_v04(size_t m, size_t n, size_t k, T const* alpha,
T const* A, size_t lda, T const* B, size_t ldb,
T const* beta, T* C, size_t ldc,
cudaStream_t stream)
{
// 可以自由调整块分块大小
// 算法的正确性应该始终得到保证
constexprunsignedint BLOCK_TILE_SIZE_X{128U}; // 块分块X维度大小
constexprunsignedint BLOCK_TILE_SIZE_Y{128U}; // 块分块Y维度大小
constexprunsignedint BLOCK_TILE_SIZE_K{16U}; // 块分块K维度大小
// 每个线程计算THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y个C矩阵的值
constexprunsignedint THREAD_TILE_SIZE_X{8U}; // 线程分块X维度大小
constexprunsignedint THREAD_TILE_SIZE_Y{8U}; // 线程分块Y维度大小
// 计算每个块的线程数
constexprunsignedint NUM_THREADS_PER_BLOCK{
BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y /
(THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y)};
// 静态断言确保参数配置的正确性
static_assert(BLOCK_TILE_SIZE_X % THREAD_TILE_SIZE_X == 0U);
static_assert(BLOCK_TILE_SIZE_Y % THREAD_TILE_SIZE_Y == 0U);
static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_K == 0U);
static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_X == 0U);
static_assert(
BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_K % NUM_THREADS_PER_BLOCK == 0U);
static_assert(
BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_Y % NUM_THREADS_PER_BLOCK == 0U);
// 配置CUDA内核启动参数
dim3 const block_dim{NUM_THREADS_PER_BLOCK, 1U, 1U}; // 块维度
dim3 const grid_dim{
(static_cast<unsignedint>(n) + BLOCK_TILE_SIZE_X - 1U) /
BLOCK_TILE_SIZE_X,
(static_cast<unsignedint>(m) + BLOCK_TILE_SIZE_Y - 1U) /
BLOCK_TILE_SIZE_Y,
1U}; // 网格维度
// 启动CUDA内核
gemm_v04<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K,
THREAD_TILE_SIZE_X, THREAD_TILE_SIZE_Y>
<<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B, ldb,
*beta, C, ldc);
CHECK_LAST_CUDA_ERROR();
}
这个FP32 GEMM实现的性能在NVIDIA GeForce RTX 3090 GPU上达到13.02 TFLOPS。
具有2D块分块和2D线程分块和向量化内存访问的实现
在我的上一篇文章“CUDA向量化内存访问”中,我展示了如何使用向量化内存访问来提高一个简单的内存复制内核的性能。向量化内存访问减少了内存事务的数量,从而提高了内存带宽利用率。同样的技巧可以应用于这个GEMM内核,以加速从全局内存到共享内存的数据加载和从共享内存到寄存器的数据加载。
在之前的实现中,为了计算矩阵乘法,每个线程必须从共享内存中读取矩阵的一列和矩阵的一行,并将它们缓存在寄存器中。因为从矩阵的一列读取数据会阻止向量化内存访问,我们希望在从全局内存加载数据到共享内存时转置矩阵,这样每个线程就可以以向量化方式从共享内存中访问转置矩阵的一行和矩阵的一行,并将它们缓存在寄存器中。
下面是使用2D块分块和2D线程分块和向量化内存访问的实现。
// 向量化内存访问的数据加载函数,将矩阵A转置后加载到共享内存
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
size_t BLOCK_TILE_SIZE_K, size_t NUM_THREADS, size_t BLOCK_TILE_SKEW_SIZE_X = 0U, size_t BLOCK_TILE_SKEW_SIZE_Y = 0U, typename VECTOR_TYPE = int4>
__device__ void load_data_to_shared_memory_transposed_vectorized(T const* A, size_t lda,
T const* B, size_t ldb,
T A_thread_block_tile_transposed[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_Y + BLOCK_TILE_SKEW_SIZE_Y],
T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X + BLOCK_TILE_SKEW_SIZE_X],
size_t thread_block_tile_idx,
size_t thread_linear_idx,
size_t m, size_t n,
size_t k)
{
// 计算向量化访问的单元数量(例如int4包含4个float)
constexprsize_t NUM_VECTOR_UNITS{sizeof(VECTOR_TYPE) / sizeof(T)};
static_assert(sizeof(VECTOR_TYPE) % sizeof(T) == 0U);
static_assert(BLOCK_TILE_SIZE_K % NUM_VECTOR_UNITS == 0U);
static_assert(BLOCK_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);
// 计算向量化后的块分块大小
constexprsize_t VECTORIZED_BLOCK_TILE_SIZE_K{BLOCK_TILE_SIZE_K /
NUM_VECTOR_UNITS};
static_assert(BLOCK_TILE_SIZE_K % NUM_VECTOR_UNITS == 0U);
constexprsize_t VECTORIZED_BLOCK_TILE_SIZE_X{BLOCK_TILE_SIZE_X /
NUM_VECTOR_UNITS};
static_assert(BLOCK_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);
// 确保共享内存中的数据对齐正确,以支持向量化加载
// skew大小可能会影响向量化加载时共享内存中的数据对齐
static_assert((BLOCK_TILE_SIZE_Y) * sizeof(T) % sizeof(VECTOR_TYPE) == 0U);
static_assert((BLOCK_TILE_SIZE_X) * sizeof(T) % sizeof(VECTOR_TYPE) == 0U);
static_assert((BLOCK_TILE_SIZE_Y + BLOCK_TILE_SKEW_SIZE_Y) * sizeof(T) % sizeof(VECTOR_TYPE) == 0U);
static_assert((BLOCK_TILE_SIZE_X + BLOCK_TILE_SKEW_SIZE_X) * sizeof(T) % sizeof(VECTOR_TYPE) == 0U);
// 从DRAM中的矩阵A加载数据到共享内存中的A_thread_block_tile(转置存储)
#pragma unroll
for (size_t load_idx{0U};
load_idx < (BLOCK_TILE_SIZE_Y * VECTORIZED_BLOCK_TILE_SIZE_K +
NUM_THREADS - 1U) /
NUM_THREADS;
++load_idx)
{
// 计算当前线程在A_thread_block_tile中的行索引
size_tconst A_thread_block_tile_row_idx{
(thread_linear_idx + load_idx * NUM_THREADS) /
VECTORIZED_BLOCK_TILE_SIZE_K};
// 计算当前线程在A_thread_block_tile中的列索引(向量化后)
size_tconst A_thread_block_tile_col_idx{
(thread_linear_idx + load_idx * NUM_THREADS) %
VECTORIZED_BLOCK_TILE_SIZE_K * NUM_VECTOR_UNITS};
// 计算在全局矩阵A中的行索引
size_tconst A_row_idx{blockIdx.y * BLOCK_TILE_SIZE_Y +
A_thread_block_tile_row_idx};
// 计算在全局矩阵A中的列索引
size_tconst A_col_idx{thread_block_tile_idx * BLOCK_TILE_SIZE_K +
A_thread_block_tile_col_idx};
// 边界检查可能会在一定程度上降低内核性能
// 但它们保证了内核对所有不同GEMM配置的正确性
int4 A_row_vector_vals{0, 0, 0, 0};
if (A_row_idx < m && A_col_idx < k)
{
// 向量化读取矩阵A的一行数据
A_row_vector_vals = *reinterpret_cast<int4 const*>(
&A[A_row_idx * lda + A_col_idx]);
}
// 如果超出矩阵边界,需要将无效元素置零
if (A_col_idx + NUM_VECTOR_UNITS > k)
{
// 计算最后一个向量中无效元素的数量
size_tconst num_invalid_elements{A_col_idx + NUM_VECTOR_UNITS -
k};
// 屏蔽无效元素
T* const A_row_vector_vals_ptr{
reinterpret_cast<T*>(&A_row_vector_vals)};
for (size_t i{0U}; i < num_invalid_elements; ++i)
{
A_row_vector_vals_ptr[NUM_VECTOR_UNITS - 1U - i] =
static_cast<T>(0);
}
}
// 如果满足以下条件,可以移除下面的if判断
// static_assert(VECTORIZED_BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_Y %
// NUM_THREADS ==
// 0U);
if (A_thread_block_tile_row_idx < BLOCK_TILE_SIZE_Y &&
A_thread_block_tile_col_idx < BLOCK_TILE_SIZE_K)
{
// 将向量化读取的数据转置存储到共享内存中
for (size_t i{0U}; i < NUM_VECTOR_UNITS; ++i)
{
A_thread_block_tile_transposed
[A_thread_block_tile_col_idx + i]
[A_thread_block_tile_row_idx] =
reinterpret_cast<T const*>(&A_row_vector_vals)[i];
}
}
}
// 从DRAM中的矩阵B加载数据到共享内存中的B_thread_block_tile
#pragma unroll
for (size_t load_idx{0U};
load_idx < (BLOCK_TILE_SIZE_K * VECTORIZED_BLOCK_TILE_SIZE_X +
NUM_THREADS - 1U) /
NUM_THREADS;
++load_idx)
{
// 计算当前线程在B_thread_block_tile中的行索引
size_tconst B_thread_block_tile_row_idx{
(thread_linear_idx + load_idx * NUM_THREADS) /
VECTORIZED_BLOCK_TILE_SIZE_X};
// 计算当前线程在B_thread_block_tile中的列索引(向量化后)
size_tconst B_thread_block_tile_col_idx{
(thread_linear_idx + load_idx * NUM_THREADS) %
VECTORIZED_BLOCK_TILE_SIZE_X * NUM_VECTOR_UNITS};
// 计算在全局矩阵B中的行索引
size_tconst B_row_idx{thread_block_tile_idx * BLOCK_TILE_SIZE_K +
B_thread_block_tile_row_idx};
// 计算在全局矩阵B中的列索引
size_tconst B_col_idx{blockIdx.x * BLOCK_TILE_SIZE_X +
B_thread_block_tile_col_idx};
// 边界检查可能会在一定程度上降低内核性能
// 但它们保证了内核对所有不同GEMM配置的正确性
int4 B_row_vector_vals{0, 0, 0, 0};
if (B_row_idx < k && B_col_idx < n)
{
// 向量化读取矩阵B的一行数据
B_row_vector_vals = *reinterpret_cast<int4 const*>(
&B[B_row_idx * ldb + B_col_idx]);
}
// 如果超出矩阵边界,需要将无效元素置零
if (B_col_idx + NUM_VECTOR_UNITS > n)
{
// 计算最后一个向量中无效元素的数量
size_tconst num_invalid_elements{B_col_idx + NUM_VECTOR_UNITS -
n};
// 屏蔽无效元素
T* const B_row_vector_vals_ptr{
reinterpret_cast<T*>(&B_row_vector_vals)};
for (size_t i{0U}; i < num_invalid_elements; ++i)
{
B_row_vector_vals_ptr[NUM_VECTOR_UNITS - 1U - i] =
static_cast<T>(0);
}
}
// 如果满足以下条件,可以移除下面的if判断
// static_assert(VECTORIZED_BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_K %
// NUM_THREADS ==
// 0U);
if (B_thread_block_tile_row_idx < BLOCK_TILE_SIZE_K &&
B_thread_block_tile_col_idx < BLOCK_TILE_SIZE_X)
{
// 向量化写入到共享内存中的B_thread_block_tile
*reinterpret_cast<int4*>(
&B_thread_block_tile[B_thread_block_tile_row_idx]
[B_thread_block_tile_col_idx]) =
B_row_vector_vals;
}
}
}
// GEMM内核v05版本 - 使用向量化内存访问
// 从全局内存进行合并读写
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
size_t BLOCK_TILE_SIZE_K, size_t THREAD_TILE_SIZE_X,
size_t THREAD_TILE_SIZE_Y>
__global__ void gemm_v05_vectorized(size_t m, size_t n, size_t k, T alpha,
T const* A, size_t lda, T const* B,
size_t ldb, T beta, T* C, size_t ldc)
{
// 避免使用blockDim.x * blockDim.y作为每个块的线程数
// 因为它是运行时常量,编译器无法基于此优化循环展开
// 使用编译时常量代替
constexprsize_t NUM_THREADS{BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y /
(THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y)};
// 计算当前线程在块内的线性索引
size_tconst thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};
// 在共享内存中缓存A和B的分块以实现数据重用
__shared__ T
A_thread_block_tile_transposed[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_Y];
__shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X];
// 计算需要处理的线程块分块数量
size_tconst num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
BLOCK_TILE_SIZE_K};
// 块中的每个线程处理THREAD_TILE_SIZE_Y * THREAD_TILE_SIZE_X个输出值
// 具体来说,这些值对应于
// C[blockIdx.y * BLOCK_TILE_SIZE_Y + threadIdx.x / BLOCK_TILE_SIZE_X *
// THREAD_TILE_SIZE_Y : blockIdx.y * BLOCK_TILE_SIZE_Y + (threadIdx.x /
// BLOCK_TILE_SIZE_X + 1) * THREAD_TILE_SIZE_Y][blockIdx.x *
// BLOCK_TILE_SIZE_X + threadIdx.x % BLOCK_TILE_SIZE_X *
// THREAD_TILE_SIZE_X : blockIdx.x * BLOCK_TILE_SIZE_X + (threadIdx.x %
// BLOCK_TILE_SIZE_X + 1) * THREAD_TILE_SIZE_X]
T C_thread_results[THREAD_TILE_SIZE_Y][THREAD_TILE_SIZE_X] = {
static_cast<T>(0)};
// A_vals缓存在寄存器中
T A_vals[THREAD_TILE_SIZE_Y] = {static_cast<T>(0)};
// B_vals缓存在寄存器中
T B_vals[THREAD_TILE_SIZE_X] = {static_cast<T>(0)};
// 向量化访问相关的常量定义
constexprsize_t NUM_VECTOR_UNITS{sizeof(int4) / sizeof(T)};
static_assert(sizeof(int4) % sizeof(T) == 0U);
static_assert(BLOCK_TILE_SIZE_K % NUM_VECTOR_UNITS == 0U);
static_assert(BLOCK_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);
constexprsize_t VECTORIZED_THREAD_TILE_SIZE_X{THREAD_TILE_SIZE_X /
NUM_VECTOR_UNITS};
static_assert(THREAD_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);
// 主计算循环:遍历所有线程块分块
for (size_t thread_block_tile_idx{0U};
thread_block_tile_idx < num_thread_block_tiles;
++thread_block_tile_idx)
{
// 加载数据到共享内存(A转置,B正常)
load_data_to_shared_memory_transposed_vectorized<
T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K,
NUM_THREADS>(A, lda, B, ldb, A_thread_block_tile_transposed,
B_thread_block_tile, thread_block_tile_idx,
thread_linear_idx, m, n, k);
__syncthreads();
// 在K维度上进行矩阵乘法计算
#pragma unroll
for (size_t k_i{0U}; k_i < BLOCK_TILE_SIZE_K; ++k_i)
{
// 计算当前线程在A_thread_block_tile中的行索引
size_tconst A_thread_block_tile_row_idx{
thread_linear_idx / (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
THREAD_TILE_SIZE_Y};
// A的列索引就是当前的k_i
size_tconst A_thread_block_tile_col_idx{k_i};
// 从共享内存中加载A的数据到寄存器
#pragma unroll
for (size_t thread_tile_row_idx{0U};
thread_tile_row_idx < THREAD_TILE_SIZE_Y;
++thread_tile_row_idx)
{
A_vals[thread_tile_row_idx] =
A_thread_block_tile_transposed[A_thread_block_tile_col_idx]
[A_thread_block_tile_row_idx +
thread_tile_row_idx];
}
// 计算当前线程在B_thread_block_tile中的索引
size_tconst B_thread_block_tile_row_idx{k_i};
size_tconst B_thread_block_tile_col_idx{
thread_linear_idx % (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
THREAD_TILE_SIZE_X};
// 虽然从A_thread_block_tile的读取无法向量化,但从B_thread_block_tile的读取可以向量化
#pragma unroll
for (size_t thread_tile_col_vector_idx{0U};
thread_tile_col_vector_idx < VECTORIZED_THREAD_TILE_SIZE_X;
++thread_tile_col_vector_idx)
{
// 向量化读取B的数据到寄存器
*reinterpret_cast<int4*>(
&B_vals[thread_tile_col_vector_idx * NUM_VECTOR_UNITS]) =
*reinterpret_cast<int4 const*>(
&B_thread_block_tile[B_thread_block_tile_row_idx]
[B_thread_block_tile_col_idx +
thread_tile_col_vector_idx *
NUM_VECTOR_UNITS]);
}
// 执行矩阵乘法累加计算
for (size_t thread_tile_row_idx{0U};
thread_tile_row_idx < THREAD_TILE_SIZE_Y;
++thread_tile_row_idx)
{
for (size_t thread_tile_col_idx{0U};
thread_tile_col_idx < THREAD_TILE_SIZE_X;
++thread_tile_col_idx)
{
C_thread_results[thread_tile_row_idx]
[thread_tile_col_idx] +=
A_vals[thread_tile_row_idx] *
B_vals[thread_tile_col_idx];
}
}
}
__syncthreads();
}
// 向量化写入结果到DRAM
for (size_t thread_tile_row_idx{0U};
thread_tile_row_idx < THREAD_TILE_SIZE_Y; ++thread_tile_row_idx)
{
for (size_t thread_tile_col_vector_idx{0U};
thread_tile_col_vector_idx < VECTORIZED_THREAD_TILE_SIZE_X;
++thread_tile_col_vector_idx)
{
// 计算在全局矩阵C中的行索引
size_tconst C_row_idx{
blockIdx.y * BLOCK_TILE_SIZE_Y +
thread_linear_idx / (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
THREAD_TILE_SIZE_Y +
thread_tile_row_idx};
// 计算在全局矩阵C中的列索引
size_tconst C_col_idx{
blockIdx.x * BLOCK_TILE_SIZE_X +
thread_linear_idx % (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
THREAD_TILE_SIZE_X +
thread_tile_col_vector_idx * NUM_VECTOR_UNITS};
// 向量化读取C的原始值
int4 C_row_vector_vals{*reinterpret_cast<int4 const*>(
&C[C_row_idx * ldc + C_col_idx])};
// 向量化读取计算结果
int4 const C_thread_results_row_vector_vals{
*reinterpret_cast<int4 const*>(
&C_thread_results[thread_tile_row_idx]
[thread_tile_col_vector_idx *
NUM_VECTOR_UNITS])};
// 更新C_row_vector_vals中的值(执行alpha*结果 + beta*原值)
for (size_t i{0U}; i < NUM_VECTOR_UNITS; ++i)
{
reinterpret_cast<T*>(&C_row_vector_vals)[i] =
alpha * reinterpret_cast<T const*>(
&C_thread_results_row_vector_vals)[i] +
beta * reinterpret_cast<T const*>(&C_row_vector_vals)[i];
}
// 向量化写入到C
if (C_row_idx < m && C_col_idx < n)
{
// 不需要屏蔽越界的无效元素,
// 因为C矩阵的行是32字节对齐的
*reinterpret_cast<int4*>(&C[C_row_idx * ldc + C_col_idx]) =
C_row_vector_vals;
}
}
}
}
// 启动GEMM内核v05向量化版本的函数
template <typename T>
void launch_gemm_kernel_v05_vectorized(size_t m, size_t n, size_t k,
T const* alpha, T const* A, size_t lda,
T const* B, size_t ldb, T const* beta,
T* C, size_t ldc, cudaStream_t stream)
{
// 可以自由调整块分块大小
// 算法正确性应该始终得到保证
constexprunsignedint BLOCK_TILE_SIZE_X{128U}; // 块分块X维度大小
constexprunsignedint BLOCK_TILE_SIZE_Y{128U}; // 块分块Y维度大小
constexprunsignedint BLOCK_TILE_SIZE_K{16U}; // 块分块K维度大小
// 每个线程计算THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y个C矩阵的值
constexprunsignedint THREAD_TILE_SIZE_X{8U}; // 线程分块X维度大小
constexprunsignedint THREAD_TILE_SIZE_Y{8U}; // 线程分块Y维度大小
// 计算每个块的线程数
constexprunsignedint NUM_THREADS_PER_BLOCK{
BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y /
(THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y)};
// 静态断言确保参数配置的正确性
static_assert(BLOCK_TILE_SIZE_X % THREAD_TILE_SIZE_X == 0U);
static_assert(BLOCK_TILE_SIZE_Y % THREAD_TILE_SIZE_Y == 0U);
static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_K == 0U);
static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_X == 0U);
static_assert(
BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_K % NUM_THREADS_PER_BLOCK == 0U);
static_assert(
BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_Y % NUM_THREADS_PER_BLOCK == 0U);
// 配置CUDA内核启动参数
dim3 const block_dim{NUM_THREADS_PER_BLOCK, 1U, 1U}; // 块维度
dim3 const grid_dim{
(static_cast<unsignedint>(n) + BLOCK_TILE_SIZE_X - 1U) /
BLOCK_TILE_SIZE_X,
(static_cast<unsignedint>(m) + BLOCK_TILE_SIZE_Y - 1U) /
BLOCK_TILE_SIZE_Y,
1U}; // 网格维度
// 启动CUDA内核
gemm_v05_vectorized<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
BLOCK_TILE_SIZE_K, THREAD_TILE_SIZE_X,
THREAD_TILE_SIZE_Y>
<<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B, ldb,
*beta, C, ldc);
CHECK_LAST_CUDA_ERROR();
}
除了使用向量化内存访问加载数据外,其余内核与之前使用2D块分块和2D线程分块的实现相同。然而,在我们的使用案例中,向量化内存访问存在一个在之前实现中不存在的注意事项。当我们将数据从全局内存加载到共享内存,并将数据从共享内存加载到寄存器时,考虑到矩阵是2D的,我们需要确保向量化内存访问数据类型的数据对齐是正确的。否则,将会发生未定义行为。例如,如果我们使用 作为向量化内存访问数据类型,我们需要确保数据对齐是16字节的倍数。这就是为什么我们必须填充矩阵 和矩阵 在全局内存中的前导维度,并且共享内存维度必须仔细选择。
这个FP32 GEMM实现的性能在NVIDIA GeForce RTX 3090 GPU上达到19.66 TFLOPS。
使用2D块分块和2D Warp分块和2D线程分块和向量化内存访问的实现
在CUDA编程模型中,warp由32个线程组成,是调度和执行的最小单位。当warp中的线程访问共享内存的同一个bank时,可能会发生共享内存bank冲突(https://leimao.github.io/blog/CUDA-Shared-Memory-Bank-Conflicts/)。在我们之前的实现中,由于GEMM CUDA内核不是以warp为中心的方式组织的,如何避免共享内存bank冲突并不明显。
在这个实现中,我们将以warp为中心的方式组织GEMM CUDA内核,并使用2D warp分块和2D线程分块,以便可以更容易地预期和优化共享内存bank冲突。
理解warp分块几乎与理解线程分块完全相同。
数学上,给定矩阵乘法和累加操作 ,其中 ,,,,矩阵可以被分成更小的矩阵。
中的每个小矩阵都作为多个小矩阵乘法和累加来计算。
每个具有块warp索引 的warp,其中 和 ,在具有块索引 的块中,其中 和 ,负责计算一个小矩阵乘法和累加 。
到目前为止,一切看起来都与2D线程分块的数学描述相同,只是线程索引和线程分块大小被warp索引和warp分块大小所替代。
剩下的问题是如何使用warp中具有块warp索引 的所有32个线程来计算 。做到这一点并没有唯一的方法。我们选择的方式是使用2D线程分块。假设warp中行的线程数为 ,列的线程数为 ,我们必须有 。warp中的每个线程应该负责计算 个输出矩阵的值。我们接着将线程分块大小设置为行为 ,列为 ,使得 和 。warp中的每个线程将必须计算 个大小为 的输出矩阵 的块。
假设线程分块索引为 ,其中 和 。负责计算该分块的线程具有warp线程索引 。因为矩阵 可以沿行维度分成 个片段,矩阵 可以沿列维度分成 个片段。我们有
每个具有warp线程索引 的线程负责计算一个小矩阵乘法和累加 。
线程分块 可以按如下方式计算。
综合起来,线程分块 可以按如下方式计算。
在此实现中,我们设置 以使线程分块算法更简单。
下面是使用2D块分块和2D warp分块和2D线程分块和向量化内存访问的实现。
// GEMM kernel v06.
// 每个线程块中的线程处理 THREAD_TILE_SIZE_Y * THREAD_TILE_SIZE_X 个输出值
// 线程数量为 BLOCK_TILE_SIZE_Y * BLOCK_TILE_SIZE_X / (THREAD_TILE_SIZE_Y * THREAD_TILE_SIZE_X)
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
size_t BLOCK_TILE_SIZE_K, size_t WARP_TILE_SIZE_X,
size_t WARP_TILE_SIZE_Y, size_t THREAD_TILE_SIZE_X,
size_t THREAD_TILE_SIZE_Y, size_t NUM_THREADS_PER_WARP_X,
size_t NUM_THREADS_PER_WARP_Y>
__global__ void gemm_v06_vectorized(size_t m, size_t n, size_t k, T alpha,
T const* A, size_t lda, T const* B,
size_t ldb, T beta, T* C, size_t ldc)
{
// 确保每个warp有32个线程
static_assert(NUM_THREADS_PER_WARP_X * NUM_THREADS_PER_WARP_Y == 32U);
// 计算每个块中warp的数量
constexprsize_t NUM_WARPS_X{BLOCK_TILE_SIZE_X / WARP_TILE_SIZE_X};
static_assert(BLOCK_TILE_SIZE_X % WARP_TILE_SIZE_X == 0U);
constexprsize_t NUM_WARPS_Y{BLOCK_TILE_SIZE_Y / WARP_TILE_SIZE_Y};
static_assert(BLOCK_TILE_SIZE_Y % WARP_TILE_SIZE_Y == 0U);
// 计算每个warp中线程块的数量
constexprunsignedint NUM_THREAD_TILES_PER_WARP_X{
WARP_TILE_SIZE_X / (THREAD_TILE_SIZE_X * NUM_THREADS_PER_WARP_X)};
constexprunsignedint NUM_THREAD_TILES_PER_WARP_Y{
WARP_TILE_SIZE_Y / (THREAD_TILE_SIZE_Y * NUM_THREADS_PER_WARP_Y)};
static_assert(
WARP_TILE_SIZE_X % (THREAD_TILE_SIZE_X * NUM_THREADS_PER_WARP_X) == 0U);
static_assert(
WARP_TILE_SIZE_Y % (THREAD_TILE_SIZE_Y * NUM_THREADS_PER_WARP_Y) == 0U);
// 计算总的线程数量
constexprunsignedint NUM_THREADS_X{NUM_WARPS_X * NUM_THREADS_PER_WARP_X};
constexprunsignedint NUM_THREADS_Y{NUM_WARPS_Y * NUM_THREADS_PER_WARP_Y};
// 避免使用 blockDim.x * blockDim.y 作为每个块的线程数
// 因为它是运行时常量,编译器无法基于此优化循环展开
// 使用编译时常量代替
constexprsize_t NUM_THREADS{NUM_THREADS_X * NUM_THREADS_Y};
// 在共享内存中缓存A和B的块以实现数据重用
__shared__ T
A_thread_block_tile_transposed[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_Y];
__shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X];
// A_vals 缓存在寄存器中
T A_vals[NUM_THREAD_TILES_PER_WARP_Y][THREAD_TILE_SIZE_Y] = {
static_cast<T>(0)};
// B_vals 缓存在寄存器中
T B_vals[NUM_THREAD_TILES_PER_WARP_X][THREAD_TILE_SIZE_X] = {
static_cast<T>(0)};
// 计算线程索引
size_tconst thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};
size_tconst warp_linear_idx{thread_linear_idx / 32U};
size_tconst warp_row_idx{warp_linear_idx / NUM_WARPS_X};
size_tconst warp_col_idx{warp_linear_idx % NUM_WARPS_X};
size_tconst thread_linear_idx_in_warp{thread_linear_idx % 32U};
size_tconst thread_linear_row_idx_in_warp{thread_linear_idx_in_warp /
NUM_THREADS_PER_WARP_X};
size_tconst thread_linear_col_idx_in_warp{thread_linear_idx_in_warp %
NUM_THREADS_PER_WARP_X};
// 执行内积求和的外层循环次数
// C_thread_block_tile =
// \sigma_{thread_block_tile_idx=0}^{num_thread_block_tiles-1} A[:,
// thread_block_tile_idx:BLOCK_TILE_SIZE_K] *
// B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :]
size_tconst num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
BLOCK_TILE_SIZE_K};
// 块中的每个线程处理 NUM_THREAD_TILES_PER_WARP_Y *
// NUM_THREAD_TILES_PER_WARP_X * THREAD_TILE_SIZE_Y *
// THREAD_TILE_SIZE_X 个输出值
T C_thread_results[NUM_THREAD_TILES_PER_WARP_Y][NUM_THREAD_TILES_PER_WARP_X]
[THREAD_TILE_SIZE_Y][THREAD_TILE_SIZE_X] = {
static_cast<T>(0)};
// 向量化内存访问的设置
constexprsize_t NUM_VECTOR_UNITS{sizeof(int4) / sizeof(T)};
static_assert(sizeof(int4) % sizeof(T) == 0U);
static_assert(BLOCK_TILE_SIZE_K % NUM_VECTOR_UNITS == 0U);
static_assert(BLOCK_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);
constexprsize_t VECTORIZED_THREAD_TILE_SIZE_X{THREAD_TILE_SIZE_X /
NUM_VECTOR_UNITS};
static_assert(THREAD_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);
constexprsize_t VECTORIZED_THREAD_TILE_SIZE_Y{THREAD_TILE_SIZE_Y /
NUM_VECTOR_UNITS};
static_assert(THREAD_TILE_SIZE_Y % NUM_VECTOR_UNITS == 0U);
// 主循环:遍历所有线程块块
for (size_t thread_block_tile_idx{0U};
thread_block_tile_idx < num_thread_block_tiles;
++thread_block_tile_idx)
{
// 将数据加载到共享内存中(转置和向量化)
load_data_to_shared_memory_transposed_vectorized<
T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K,
NUM_THREADS>(A, lda, B, ldb, A_thread_block_tile_transposed,
B_thread_block_tile, thread_block_tile_idx,
thread_linear_idx, m, n, k);
__syncthreads();
// 执行 A[:, thread_block_tile_idx:BLOCK_TILE_SIZE_K] *
// B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :]
// 其中 A[:, thread_block_tile_idx:BLOCK_TILE_SIZE_K] 和
// B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :] 分别缓存在
// 共享内存中作为 A_thread_block_tile 和 B_thread_block_tile
// 这个内积进一步分解为 BLOCK_TILE_SIZE_K 个外积
// A_thread_block_tile * B_thread_block_tile =
// \sigma_{k_i=0}^{BLOCK_TILE_SIZE_K-1} A_thread_block_tile[:, k_i] @ B_thread_block_tile[k_i, :]
// 注意 A_thread_block_tile 和 B_thread_block_tile 都可以缓存在寄存器中
#pragma unroll
for (size_t k_i{0U}; k_i < BLOCK_TILE_SIZE_K; ++k_i)
{
// 加载A的数据到寄存器
#pragma unroll
for (size_t thread_tile_repeat_row_idx{0U};
thread_tile_repeat_row_idx < NUM_THREAD_TILES_PER_WARP_Y;
++thread_tile_repeat_row_idx)
{
size_tconst A_thread_block_tile_row_idx{
warp_row_idx * WARP_TILE_SIZE_Y +
thread_tile_repeat_row_idx *
(WARP_TILE_SIZE_Y / NUM_THREAD_TILES_PER_WARP_Y) +
thread_linear_row_idx_in_warp * THREAD_TILE_SIZE_Y};
size_tconst A_thread_block_tile_col_idx{k_i};
// 向量化加载A的数据
#pragma unroll
for (size_t thread_tile_y_vector_idx{0U};
thread_tile_y_vector_idx < VECTORIZED_THREAD_TILE_SIZE_Y;
++thread_tile_y_vector_idx)
{
*reinterpret_cast<int4*>(
&A_vals[thread_tile_repeat_row_idx]
[thread_tile_y_vector_idx * NUM_VECTOR_UNITS]) =
*reinterpret_cast<int4 const*>(
&A_thread_block_tile_transposed
[A_thread_block_tile_col_idx]
[A_thread_block_tile_row_idx +
thread_tile_y_vector_idx * NUM_VECTOR_UNITS]);
}
}
// 加载B的数据到寄存器
#pragma unroll
for (size_t thread_tile_repeat_col_idx{0U};
thread_tile_repeat_col_idx < NUM_THREAD_TILES_PER_WARP_X;
++thread_tile_repeat_col_idx)
{
size_tconst B_thread_block_tile_row_idx{k_i};
size_tconst B_thread_block_tile_col_idx{
warp_col_idx * WARP_TILE_SIZE_X +
thread_tile_repeat_col_idx *
(WARP_TILE_SIZE_X / NUM_THREAD_TILES_PER_WARP_X) +
thread_linear_col_idx_in_warp * THREAD_TILE_SIZE_X};
// 向量化加载B的数据
#pragma unroll
for (size_t thread_tile_x_vector_idx{0U};
thread_tile_x_vector_idx < VECTORIZED_THREAD_TILE_SIZE_X;
++thread_tile_x_vector_idx)
{
*reinterpret_cast<int4*>(
&B_vals[thread_tile_repeat_col_idx]
[thread_tile_x_vector_idx * NUM_VECTOR_UNITS]) =
*reinterpret_cast<int4 const*>(
&B_thread_block_tile[B_thread_block_tile_row_idx]
[B_thread_block_tile_col_idx +
thread_tile_x_vector_idx *
NUM_VECTOR_UNITS]);
}
}
// 计算 NUM_THREAD_TILES_PER_WARP_Y * NUM_THREAD_TILES_PER_WARP_X 个外积
#pragma unroll
for (size_t thread_tile_repeat_row_idx{0U};
thread_tile_repeat_row_idx < NUM_THREAD_TILES_PER_WARP_Y;
++thread_tile_repeat_row_idx)
{
#pragma unroll
for (size_t thread_tile_repeat_col_idx{0U};
thread_tile_repeat_col_idx < NUM_THREAD_TILES_PER_WARP_X;
++thread_tile_repeat_col_idx)
{
// 执行线程块级别的矩阵乘法
#pragma unroll
for (size_t thread_tile_y_idx{0U};
thread_tile_y_idx < THREAD_TILE_SIZE_Y;
++thread_tile_y_idx)
{
#pragma unroll
for (size_t thread_tile_x_idx{0U};
thread_tile_x_idx < THREAD_TILE_SIZE_X;
++thread_tile_x_idx)
{
// 累加计算结果
C_thread_results[thread_tile_repeat_row_idx]
[thread_tile_repeat_col_idx]
[thread_tile_y_idx]
[thread_tile_x_idx] +=
A_vals[thread_tile_repeat_row_idx]
[thread_tile_y_idx] *
B_vals[thread_tile_repeat_col_idx]
[thread_tile_x_idx];
}
}
}
}
}
__syncthreads();
}
// 将结果写入DRAM
#pragma unroll
for (size_t thread_tile_repeat_row_idx{0U};
thread_tile_repeat_row_idx < NUM_THREAD_TILES_PER_WARP_Y;
++thread_tile_repeat_row_idx)
{
#pragma unroll
for (size_t thread_tile_repeat_col_idx{0U};
thread_tile_repeat_col_idx < NUM_THREAD_TILES_PER_WARP_X;
++thread_tile_repeat_col_idx)
{
#pragma unroll
for (size_t thread_tile_y_idx{0U};
thread_tile_y_idx < THREAD_TILE_SIZE_Y; ++thread_tile_y_idx)
{
#pragma unroll
for (size_t thread_tile_x_vector_idx{0U};
thread_tile_x_vector_idx < VECTORIZED_THREAD_TILE_SIZE_X;
++thread_tile_x_vector_idx)
{
// 计算输出矩阵C的索引
size_tconst C_row_idx{
blockIdx.y * BLOCK_TILE_SIZE_Y +
warp_row_idx * WARP_TILE_SIZE_Y +
thread_tile_repeat_row_idx *
(WARP_TILE_SIZE_Y / NUM_THREAD_TILES_PER_WARP_Y) +
thread_linear_row_idx_in_warp * THREAD_TILE_SIZE_Y +
thread_tile_y_idx};
size_tconst C_col_idx{
blockIdx.x * BLOCK_TILE_SIZE_X +
warp_col_idx * WARP_TILE_SIZE_X +
thread_tile_repeat_col_idx *
(WARP_TILE_SIZE_X / NUM_THREAD_TILES_PER_WARP_X) +
thread_linear_col_idx_in_warp * THREAD_TILE_SIZE_X +
thread_tile_x_vector_idx * NUM_VECTOR_UNITS};
// 边界检查
if (C_row_idx < m && C_col_idx < n)
{
// 向量化读取原始C值
int4 C_vals{*reinterpret_cast<int4 const*>(
&C[C_row_idx * ldc + C_col_idx])};
// 应用alpha和beta系数,更新C值
#pragma unroll
for (size_t i{0U}; i < NUM_VECTOR_UNITS; ++i)
{
reinterpret_cast<T*>(&C_vals)[i] =
alpha *
C_thread_results[thread_tile_repeat_row_idx]
[thread_tile_repeat_col_idx]
[thread_tile_y_idx]
[thread_tile_x_vector_idx *
NUM_VECTOR_UNITS +
i] +
beta * reinterpret_cast<T const*>(&C_vals)[i];
}
// 向量化写回结果
*reinterpret_cast<int4*>(
&C[C_row_idx * ldc + C_col_idx]) = C_vals;
}
}
}
}
}
}
// 启动GEMM kernel v06向量化版本的函数
template <typename T>
void launch_gemm_kernel_v06_vectorized(size_t m, size_t n, size_t k,
T const* alpha, T const* A, size_t lda,
T const* B, size_t ldb, T const* beta,
T* C, size_t ldc, cudaStream_t stream)
{
// 可以自由调整块分块大小
// 算法正确性应该始终得到保证
constexprunsignedint BLOCK_TILE_SIZE_X{128U}; // 块在X方向的大小
constexprunsignedint BLOCK_TILE_SIZE_Y{128U}; // 块在Y方向的大小
constexprunsignedint BLOCK_TILE_SIZE_K{16U}; // 块在K方向的大小
constexprunsignedint WARP_TILE_SIZE_X{32U}; // warp在X方向的大小
constexprunsignedint WARP_TILE_SIZE_Y{64U}; // warp在Y方向的大小
constexprunsignedint NUM_WARPS_X{BLOCK_TILE_SIZE_X / WARP_TILE_SIZE_X};
constexprunsignedint NUM_WARPS_Y{BLOCK_TILE_SIZE_Y / WARP_TILE_SIZE_Y};
static_assert(BLOCK_TILE_SIZE_X % WARP_TILE_SIZE_X == 0U);
static_assert(BLOCK_TILE_SIZE_Y % WARP_TILE_SIZE_Y == 0U);
constexprunsignedint THREAD_TILE_SIZE_X{8U}; // 线程在X方向的分块大小
constexprunsignedint THREAD_TILE_SIZE_Y{8U}; // 线程在Y方向的分块大小
constexprunsignedint NUM_THREADS_PER_WARP_X{4U}; // 每个warp在X方向的线程数
constexprunsignedint NUM_THREADS_PER_WARP_Y{8U}; // 每个warp在Y方向的线程数
static_assert(NUM_THREADS_PER_WARP_X * NUM_THREADS_PER_WARP_Y == 32U);
static_assert(
WARP_TILE_SIZE_X % (THREAD_TILE_SIZE_X * NUM_THREADS_PER_WARP_X) == 0U);
static_assert(
WARP_TILE_SIZE_Y % (THREAD_TILE_SIZE_Y * NUM_THREADS_PER_WARP_Y) == 0U);
constexprunsignedint NUM_THREADS_X{NUM_WARPS_X * NUM_THREADS_PER_WARP_X};
constexprunsignedint NUM_THREADS_Y{NUM_WARPS_Y * NUM_THREADS_PER_WARP_Y};
constexprunsignedint NUM_THREADS_PER_BLOCK{NUM_THREADS_X * NUM_THREADS_Y};
// 设置块和网格维度
dim3 const block_dim{NUM_THREADS_PER_BLOCK, 1U, 1U};
dim3 const grid_dim{
(static_cast<unsignedint>(n) + BLOCK_TILE_SIZE_X - 1U) /
BLOCK_TILE_SIZE_X,
(static_cast<unsignedint>(m) + BLOCK_TILE_SIZE_Y - 1U) /
BLOCK_TILE_SIZE_Y,
1U};
// 启动kernel
gemm_v06_vectorized<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
BLOCK_TILE_SIZE_K, WARP_TILE_SIZE_X, WARP_TILE_SIZE_Y,
THREAD_TILE_SIZE_X, THREAD_TILE_SIZE_Y,
NUM_THREADS_PER_WARP_X, NUM_THREADS_PER_WARP_Y>
<<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B, ldb,
*beta, C, ldc);
CHECK_LAST_CUDA_ERROR();
}
这个FP32 GEMM实现的性能在NVIDIA GeForce RTX 3090 GPU上达到20.16 TFLOPS。与cuBLAS FP32 GEMM性能24.59 TFLOPS相比,这个实现已经优化得相当不错。
使用2D块分块和2D warp分块和Tensor Core和向量化内存访问的实现
因为我们已经以warp为中心组织了GEMM CUDA内核,并且NVIDIA Tensor Core指令在warp级别接口,因此利用NVIDIA Tensor Core(https://leimao.github.io/blog/NVIDIA-Tensor-Core-Programming/) WMMA API进一步加速GEMM计算非常简单。因为NVIDIA Tensor Core不支持IEEE FP32计算,我们将使这个CUDA内核运行FP16 GEMM。
与使用2D块分块和2D warp分块和2D线程分块和向量化内存访问的实现相比,使用2D块分块和2D warp分块和Tensor Core和向量化内存访问的实现更简单,因为线程分块过程被NVIDIA Tensor Core warp级WMMA API抽象掉了。
从数学角度来看,给定矩阵乘法和累加操作:,其中 ,,,,这些矩阵可以被分割成更小的矩阵。
中的每个小矩阵都是通过多个小矩阵乘法和累加计算得出的。
每个具有块warp索引 的warp,其中 和 ,在具有块索引 的块中,其中 和 ,负责计算一个小矩阵乘法和累加 。
假设Tensor Core WMMA GEMM的大小是 。因为矩阵 可以沿行维度分割为 个片段,矩阵 可以沿列维度分割为 个片段。我们有:
每个warp不是调用线程级指令,而是调用WMMA warp级Tensor Core来计算所有的 迭代计算 。
在这个实现中,由于WMMA Tensor Core API的限制,,,。
下面的代码片段展示了使用2D块分块、2D warp分块、Tensor Core和向量化内存访问的实现。
// GEMM kernel v07.
// 每个线程块中的每个线程处理 THREAD_TILE_SIZE_Y * THREAD_TILE_SIZE_X 个输出值
// 线程数量为 BLOCK_TILE_SIZE_Y * BLOCK_TILE_SIZE_X / (THREAD_TILE_SIZE_Y * THREAD_TILE_SIZE_X)
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
size_t BLOCK_TILE_SIZE_K, size_t BLOCK_TILE_SKEW_SIZE_X,
size_t BLOCK_TILE_SKEW_SIZE_Y, size_t WARP_TILE_SIZE_X,
size_t WARP_TILE_SIZE_Y, size_t WMMA_TILE_SIZE_X,
size_t WMMA_TILE_SIZE_Y, size_t WMMA_TILE_SIZE_K, size_t NUM_THREADS>
__global__ void gemm_v07_vectorized(size_t m, size_t n, size_t k, T alpha,
T const* A, size_t lda, T const* B,
size_t ldb, T beta, T* C, size_t ldc)
{
// 计算X方向上的warp数量
constexprsize_t NUM_WARPS_X{BLOCK_TILE_SIZE_X / WARP_TILE_SIZE_X};
// 确保块分块大小能被warp分块大小整除
static_assert(BLOCK_TILE_SIZE_X % WARP_TILE_SIZE_X == 0U);
static_assert(BLOCK_TILE_SIZE_Y % WARP_TILE_SIZE_Y == 0U);
// 在共享内存中缓存A和B的分块以实现数据重用
// A矩阵分块进行转置存储,添加skew以避免bank冲突
__shared__ T A_thread_block_tile_transposed[BLOCK_TILE_SIZE_K]
[BLOCK_TILE_SIZE_Y +
BLOCK_TILE_SKEW_SIZE_Y];
// B矩阵分块正常存储,添加skew以避免bank冲突
__shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X +
BLOCK_TILE_SKEW_SIZE_X];
// 计算每个warp在X和Y方向上的WMMA分块数量
constexprsize_t NUM_WMMA_TILES_X{WARP_TILE_SIZE_X / WMMA_TILE_SIZE_X};
static_assert(WARP_TILE_SIZE_X % WMMA_TILE_SIZE_X == 0U);
constexprsize_t NUM_WMMA_TILES_Y{WARP_TILE_SIZE_Y / WMMA_TILE_SIZE_Y};
static_assert(WARP_TILE_SIZE_Y % WMMA_TILE_SIZE_Y == 0U);
// 计算K方向上的WMMA分块数量
constexprsize_t NUM_WMMA_TILES_K{BLOCK_TILE_SIZE_K / WMMA_TILE_SIZE_K};
static_assert(BLOCK_TILE_SIZE_K % WMMA_TILE_SIZE_K == 0U);
// 声明WMMA片段
// A矩阵片段,列主序存储
nvcuda::wmma::fragment<nvcuda::wmma::matrix_a, WMMA_TILE_SIZE_Y,
WMMA_TILE_SIZE_X, WMMA_TILE_SIZE_K, T,
nvcuda::wmma::col_major>
a_frags[NUM_WMMA_TILES_Y];
// B矩阵片段,行主序存储
nvcuda::wmma::fragment<nvcuda::wmma::matrix_b, WMMA_TILE_SIZE_Y,
WMMA_TILE_SIZE_X, WMMA_TILE_SIZE_K, T,
nvcuda::wmma::row_major>
b_frags[NUM_WMMA_TILES_X];
// 累加器片段,用于存储中间计算结果
nvcuda::wmma::fragment<nvcuda::wmma::accumulator, WMMA_TILE_SIZE_Y,
WMMA_TILE_SIZE_X, WMMA_TILE_SIZE_K, T>
acc_frags[NUM_WMMA_TILES_Y][NUM_WMMA_TILES_X];
// C矩阵片段,用于加载和存储最终结果
nvcuda::wmma::fragment<nvcuda::wmma::accumulator, WMMA_TILE_SIZE_Y,
WMMA_TILE_SIZE_X, WMMA_TILE_SIZE_K, T>
c_frag;
// 确保累加器从0开始
#pragma unroll
for (size_t wmma_tile_row_idx{0U}; wmma_tile_row_idx < NUM_WMMA_TILES_Y;
++wmma_tile_row_idx)
{
for (size_t wmma_tile_col_idx{0U}; wmma_tile_col_idx < NUM_WMMA_TILES_X;
++wmma_tile_col_idx)
{
// 将累加器片段初始化为0
nvcuda::wmma::fill_fragment(
acc_frags[wmma_tile_row_idx][wmma_tile_col_idx],
static_cast<T>(0));
}
}
// 计算线程的线性索引
size_tconst thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};
// 计算warp的线性索引(每个warp有32个线程)
size_tconst warp_linear_idx{thread_linear_idx / 32U};
// 计算warp在Y方向上的索引
size_tconst warp_row_idx{warp_linear_idx / NUM_WARPS_X};
// 计算warp在X方向上的索引
size_tconst warp_col_idx{warp_linear_idx % NUM_WARPS_X};
// 计算外层循环次数,用于执行内积求和
// C_thread_block_tile =
// \sigma_{thread_block_tile_idx=0}^{num_thread_block_tiles-1} A[:,
// thread_block_tile_idx:BLOCK_TILE_SIZE_K] *
// B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :]
size_tconst num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
BLOCK_TILE_SIZE_K};
// 主循环:遍历所有K方向上的分块
for (size_t thread_block_tile_idx{0U};
thread_block_tile_idx < num_thread_block_tiles;
++thread_block_tile_idx)
{
// 将数据从全局内存加载到共享内存,使用向量化访问和转置
load_data_to_shared_memory_transposed_vectorized<
T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K,
NUM_THREADS, BLOCK_TILE_SKEW_SIZE_X, BLOCK_TILE_SKEW_SIZE_Y>(
A, lda, B, ldb, A_thread_block_tile_transposed, B_thread_block_tile,
thread_block_tile_idx, thread_linear_idx, m, n, k);
// 同步所有线程,确保数据加载完成
__syncthreads();
// 执行 A[:, thread_block_tile_idx:BLOCK_TILE_SIZE_K] *
// B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :]
// 其中A和B的分块已缓存在共享内存中
// 这个内积进一步分解为BLOCK_TILE_SIZE_K个外积
// A_thread_block_tile * B_thread_block_tile =
// \sigma_{k_i=0}^{BLOCK_TILE_SIZE_K-1} A_thread_block_tile[:, k_i] @ B_thread_block_tile[k_i, :]
#pragma unroll
for (size_t k_i{0U}; k_i < NUM_WMMA_TILES_K; ++k_i)
{
#pragma unroll
// 遍历Y方向上的所有WMMA分块
for (size_t wmma_tile_row_idx{0U};
wmma_tile_row_idx < NUM_WMMA_TILES_Y; ++wmma_tile_row_idx)
{
// 从共享内存加载A矩阵片段
nvcuda::wmma::load_matrix_sync(
a_frags[wmma_tile_row_idx],
&A_thread_block_tile_transposed[k_i * WMMA_TILE_SIZE_K]
[warp_row_idx *
WARP_TILE_SIZE_Y +
wmma_tile_row_idx *
WMMA_TILE_SIZE_Y],
BLOCK_TILE_SIZE_Y + BLOCK_TILE_SKEW_SIZE_Y);
#pragma unroll
// 遍历X方向上的所有WMMA分块
for (size_t wmma_tile_col_idx{0U};
wmma_tile_col_idx < NUM_WMMA_TILES_X; ++wmma_tile_col_idx)
{
// 这些加载操作非常慢,严重影响性能
// 从共享内存加载B矩阵片段
nvcuda::wmma::load_matrix_sync(
b_frags[wmma_tile_col_idx],
&B_thread_block_tile[k_i * WMMA_TILE_SIZE_K]
[warp_col_idx * WARP_TILE_SIZE_X +
wmma_tile_col_idx *
WMMA_TILE_SIZE_Y],
BLOCK_TILE_SIZE_X + BLOCK_TILE_SKEW_SIZE_X);
// 执行矩阵乘法累加操作
nvcuda::wmma::mma_sync(
acc_frags[wmma_tile_row_idx][wmma_tile_col_idx],
a_frags[wmma_tile_row_idx], b_frags[wmma_tile_col_idx],
acc_frags[wmma_tile_row_idx][wmma_tile_col_idx]);
}
}
}
// 同步所有线程,确保计算完成
__syncthreads();
}
// 将结果写入DRAM
#pragma unroll
for (size_t wmma_tile_row_idx{0U}; wmma_tile_row_idx < NUM_WMMA_TILES_Y;
++wmma_tile_row_idx)
{
#pragma unroll
for (size_t wmma_tile_col_idx{0U}; wmma_tile_col_idx < NUM_WMMA_TILES_X;
++wmma_tile_col_idx)
{
// 从全局内存加载C矩阵片段
nvcuda::wmma::load_matrix_sync(
c_frag,
&C[(blockIdx.y * BLOCK_TILE_SIZE_Y +
warp_row_idx * WARP_TILE_SIZE_Y +
wmma_tile_row_idx * WMMA_TILE_SIZE_Y) *
n +
blockIdx.x * BLOCK_TILE_SIZE_X +
warp_col_idx * WARP_TILE_SIZE_X +
wmma_tile_col_idx * WMMA_TILE_SIZE_X],
n, nvcuda::wmma::mem_row_major);
// 执行缩放和加法操作:C = alpha * A * B + beta * C
for (size_t i{0}; i < c_frag.num_elements; ++i)
{
c_frag.x[i] =
alpha *
acc_frags[wmma_tile_row_idx][wmma_tile_col_idx].x[i] +
beta * c_frag.x[i];
}
// 将片段存储回全局内存
nvcuda::wmma::store_matrix_sync(
&C[(blockIdx.y * BLOCK_TILE_SIZE_Y +
warp_row_idx * WARP_TILE_SIZE_Y +
wmma_tile_row_idx * WMMA_TILE_SIZE_Y) *
n +
blockIdx.x * BLOCK_TILE_SIZE_X +
warp_col_idx * WARP_TILE_SIZE_X +
wmma_tile_col_idx * WMMA_TILE_SIZE_X],
c_frag, n, nvcuda::wmma::mem_row_major);
}
}
}
// GEMM kernel v07的启动函数
template <typename T>
void launch_gemm_kernel_v07_vectorized(size_t m, size_t n, size_t k,
T const* alpha, T const* A, size_t lda,
T const* B, size_t ldb, T const* beta,
T* C, size_t ldc, cudaStream_t stream)
{
// 可以自由调整块分块大小
// 算法正确性应该始终得到保证
constexprunsignedint BLOCK_TILE_SIZE_X{128U}; // 块在X方向的分块大小
constexprunsignedint BLOCK_TILE_SIZE_Y{128U}; // 块在Y方向的分块大小
constexprunsignedint BLOCK_TILE_SIZE_K{16U}; // 块在K方向的分块大小
// skew大小用于避免共享内存中的bank冲突
constexprsize_t BLOCK_TILE_SKEW_SIZE_X{16U};
constexprsize_t BLOCK_TILE_SKEW_SIZE_Y{16U};
// warp分块大小
constexprunsignedint WARP_TILE_SIZE_X{32U}; // warp在X方向的分块大小
constexprunsignedint WARP_TILE_SIZE_Y{64U}; // warp在Y方向的分块大小
// 计算X和Y方向上的warp数量
constexprunsignedint NUM_WARPS_X{BLOCK_TILE_SIZE_X / WARP_TILE_SIZE_X};
constexprunsignedint NUM_WARPS_Y{BLOCK_TILE_SIZE_Y / WARP_TILE_SIZE_Y};
// 确保块分块大小能被warp分块大小整除
static_assert(BLOCK_TILE_SIZE_X % WARP_TILE_SIZE_X == 0U);
static_assert(BLOCK_TILE_SIZE_Y % WARP_TILE_SIZE_Y == 0U);
// WMMA分块大小(固定为16x16x16)
constexprunsignedint WMMA_TILE_SIZE_X{16U};
constexprunsignedint WMMA_TILE_SIZE_Y{16U};
constexprunsignedint WMMA_TILE_SIZE_K{16U};
// 每个块的线程数量
constexprunsignedint NUM_THREADS_PER_BLOCK{NUM_WARPS_X * NUM_WARPS_Y *
32U};
// 配置块和网格维度
dim3 const block_dim{NUM_THREADS_PER_BLOCK, 1U, 1U};
dim3 const grid_dim{
(static_cast<unsignedint>(n) + BLOCK_TILE_SIZE_X - 1U) /
BLOCK_TILE_SIZE_X,
(static_cast<unsignedint>(m) + BLOCK_TILE_SIZE_Y - 1U) /
BLOCK_TILE_SIZE_Y,
1U};
// 启动kernel
gemm_v07_vectorized<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
BLOCK_TILE_SIZE_K, BLOCK_TILE_SKEW_SIZE_X,
BLOCK_TILE_SKEW_SIZE_Y, WARP_TILE_SIZE_X,
WARP_TILE_SIZE_Y, WMMA_TILE_SIZE_X, WMMA_TILE_SIZE_Y,
WMMA_TILE_SIZE_K, NUM_THREADS_PER_BLOCK>
<<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B, ldb,
*beta, C, ldc);
CHECK_LAST_CUDA_ERROR();
}
因为基本WMMA大小是 ,所有在同一个warp中的32个线程必须协同访问缓存在共享内存中的WMMA片段。因此,共享内存bank冲突很可能发生。为了避免共享内存bank冲突,我们必须填充共享内存大小,确保共享内存bank冲突不会发生。这就是为什么我们必须使用skew大小来填充共享内存大小在leading维度。
这个FP16 GEMM实现的性能在NVIDIA GeForce RTX 3090 GPU上达到46.78 TFLOPS。与cuBLAS FP16 GEMM性能138.95 TFLOPS相比,这个实现只实现了33.7%的cuBLAS FP16 GEMM性能。我们将把这个实现的性能优化作为未来工作。
结论
我们在GEMM CUDA内核上执行的优化主要遵循“CUTLASS: Fast Linear Algebra in CUDA C++”(https://developer.nvidia.com/blog/cutlass-linear-algebra-cuda/)中的图表。
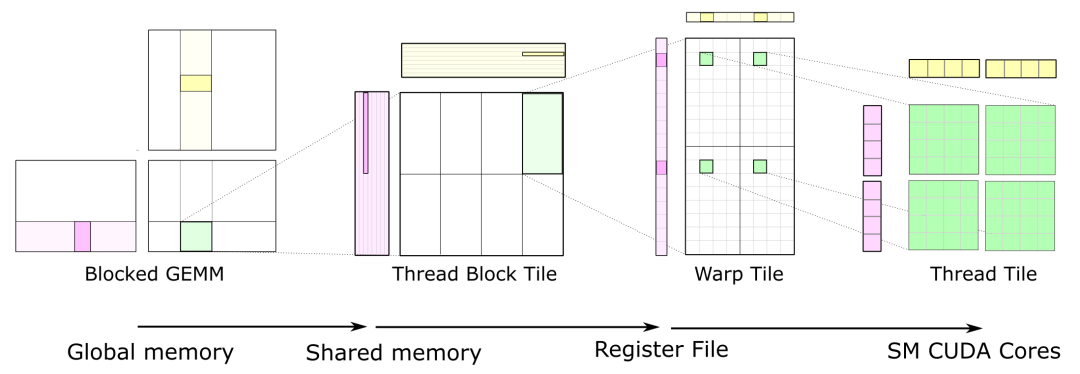
通过使用2D块分块、2D warp分块、2D线程分块和向量化内存访问等优化技术,我们可以在NVIDIA GeForce RTX 3090 GPU上实现20.16 TFLOPS FP32 GEMM性能,这大约是cuBLAS FP32 GEMM性能的80% – 90%。
源代码
GEMM CUDA内核的源代码可以在我的GitHub仓库“CUDA GEMM Optimization”(https://github.com/leimao/CUDA-GEMM-Optimization/)中找到。
参考
-
CUTLASS: Fast Linear Algebra in CUDA C++(https://developer.nvidia.com/blog/cutlass-linear-algebra-cuda/) -
CUDA GEMM Optimization – GitHub(https://github.com/leimao/CUDA-GEMM-Optimization/) -
CUDA Matrix Multiplication(https://leimao.github.io/blog/CUDA-Matrix-Multiplication/) -
CUDA Vectorized Memory Access(https://leimao.github.io/blog/CUDA-Vectorized-Memory-Access/) -
CUDA Data Alignment(https://leimao.github.io/blog/CUDA-Data-Alignment/) -
CUDA Shared Memory Bank(https://leimao.github.io/blog/CUDA-Shared-Memory-Bank/) -
NVIDIA Tensor Core Programming(https://leimao.github.io/blog/NVIDIA-Tensor-Core-Programming/) -
CUDA Tensor Core GEMM(https://github.com/NVIDIA/cuda-samples/blob/e8568c417356f7e66bb9b7130d6be7e55324a519/Samples/3_CUDA_Features/cudaTensorCoreGemm/cudaTensorCoreGemm.cu) -
How to Optimize a CUDA Matmul Kernel for cuBLAS-like Performance: a Worklog(https://siboehm.com/articles/22/CUDA-MMM)
(文:GiantPandaCV)

