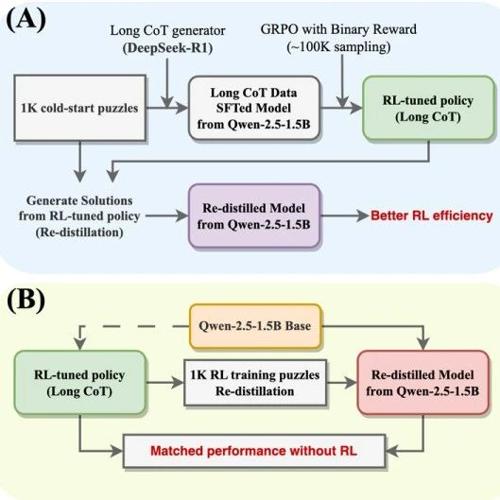
论文：Towards Revealing the Effectiveness of Small-Scale Fine-tuning in R1-style Reinforcement Learning
Abs：https://arxiv.org/abs/2505.17988
复现代码github链接：https://github.com/on1262/deep-reasoning

主要结论

RL过程是“可压缩”的

我们提出一种解释性方法(re-distillation, 重蒸镏)，用1K样本SFT可达到与R1-style RL相同的泛化性能，而后者采样次数超过100K。可压缩性质说明RL并非天然具有内在的泛化性优势，SFT也并非天然缺乏泛化能力。

小规模SFT做冷启动很重要

RL前使用1K样本做SFT将显著影响RL收敛曲线，从instruct或base模型训练都不是最优选择。通过选择合适的冷启动数据集，我们在K&K数据集上使用1.5B模型成功达到了超越DeepSeek-V3-0324的泛化性能，并且没有使用课程学习等trick

从理论上解释样本质量与泛化能力的关系

我们基于线性化假设下的kernel method解释单个样本如何影响泛化能力，并定义了一个可计算的sample effect。实验中，效果最好的SFT样本并非具有最佳的深度思考模式，而是具有更高的sample effect

从理论上解释Re-distillation为何高效

我们从理论上解释re-distillation方法为何能仅用SFT达到如此好的泛化效果，这并非一两个数据集上的偶然现象，而是RL过程在理论上会提升输出样本的sample effect

RL探索应该依靠SFT而不是随机性

我们发现RL天然地不擅长探索，在RL过程中，输出模式从尾部开始改变，逐渐向前移动。靠前的token对输出模式影响很大，却难以被改变。基于小规模SFT改变输出模式显著优于基于randomness的探索，对RL收敛影响很大。

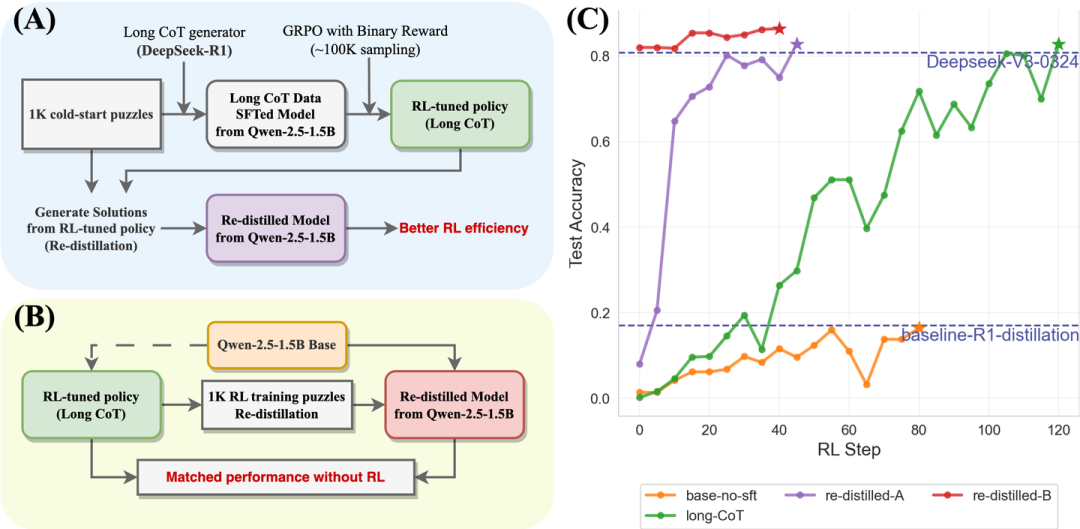
初步探索：小规模SFT如何影响RL过程

DeepSeek-R1描绘了一个具有吸引力的图景：R1-Zero说明GRPO无需SFT即可实现模型的自我进步，R1使用高质量数据冷启动增强输出可读性，本质的性能提升来自于RL中的自我试错。近来也有坚持zero-RL的工作，直接从base/instruct模型开始训练。然而，LLM的pretraining和SFT都使用CELoss，并没有本质上的区别。如果模型的输出模式被最后1K SFT数据主导会如何？ 那么从base model能直接成功RL的原因可能是最后的1K pretrain sample恰好激发了深度思考的模式。为了检验这个假设，我们第一步验证小规模SFT是否对RL具有显著影响。

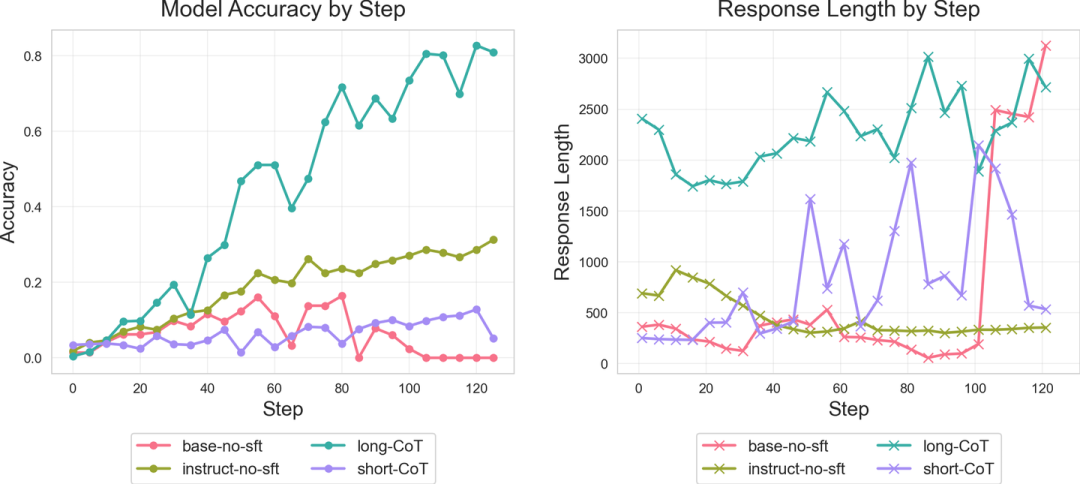
我们定义小规模SFT为少于2K样本，这旨在确保SFT的性能提升来自于模型内在能力的激发，而非持续预训练。在K&K数据集上，long-CoT从DeepSeek-R1蒸镏1K数据并只取正确样本，short-CoT采用KK数据集自带的程序生成CoT，为了对照加入base/instruct直接做RL的实验，所有实验均在Qwen2.5-1.5B上进行，RL算法为GRPO。结果显示小规模SFT对RL具有显著影响，只有long-CoT能达到0.8的test acc，并且保持较高且有意义的长CoT。是否long-CoT就一定好于其他方法？在MATH数据集上，long-CoT略差于从base直接训练，这种优越性并不是稳定的。

我们还发现SFT后的性能与RL后的性能没有直接关联：KK数据集上所有初始化方法在SFT后test accuracy都低于5%，但是收敛速度和RL效率显著不同。MATH数据集上short-CoT初始acc最高但RL效果反而最差。

理论分析：什么决定了小规模SFT的effectiveness？

我们比较关心为什么这种差异存在且如此显著。一个简单的假设是SFT质量越高越好，DeepSeek-R1生成的SFT数据比Qwen2.5-1.5B模型生成的或程序自动生成的SFT数据更好，因为它包含更多的深层思考模式。接下来，我们从理论上进行分析，并最终用实验证明：如果限定只用1K样本SFT，从DeepSeek-R1蒸镏远没有达到学习效率的上限，而且存在一个简单的post-hoc方法能产生效率更高的SFT样本。这一节的详细推导可参考原文section5和附录A

使用SDE刻画RL过程中测试accuracy的增长速率

首先在理论场景中描述研究内容，在RL中，我们研究最简单的REINFORCE方法和0-1 rule-based reward，每次优化时policy采样N个样本，假设不考虑baseline而使用reward代替advantage，可以写出训练梯度的表达式：

其中N是train batch size, a是action(response), s是state(prompt)，r是0-1 binary reward。a和s都是sequence level而不是token level。

当N足够大时，由中心极限定理，每个参数的梯度均值收敛于正态分布，每个参数的协同关系通过协方差矩阵刻画。由于每次采样的参数都是随机的，我们使用随机微分方程（SDE）刻画这一过程：

其中A满足：

得到参数  随时间t变化的表达式后，就可以利用Ito lemma研究测试acc  这一统计量随时间如何演化了，我们研究测试acc的增长速率，即  。测试acc的增长速度是一个随机过程，在每个时刻具有均值（飘移项）和方差（噪声项）。只考虑它的均值（即N次实验的期望acc增长速率）如何随时间演化，这一项可以写成两项之和：

飘移项的第一项，即positive effect，表示在采样数量N趋于无穷时的期望增长速率。当训练集和测试集从同一个分布中随机采样时，Dt和De可互换，此时该项是一个随机矢量期望与自身的内积，是非负的。第二项则是噪声对学习速率的影响，它通常为负。例如，当模型收敛至最优policy时，改变任何参数都会导致性能下降，因此，海森矩阵  为负定，此时第二项一定不大于0。当降低学习率  或提升buffer大小时第二项的影响削弱，这也解释了为什么较大的学习率和较低的N往往导致RL失败。

然而，进一步推导却遇到相当大的困难。首先，第二项的海森矩阵难以计算，且多步RL的参数theta随时间变化，是非线性的。我们考虑在足够好的超参数下，第二项的系数  足够小，并且假设RL迭代step较少时，第一项的线性作用能够刻画整个RL的性质，只计算飘移项的第一项即可近似RL学习效率。事实上，在25step内Qwen2.5-1.5B即表现出显著的提升，我们在之后也会验证理论假设的有效性。

为什么不从泰勒展开/NTK或其他理论分析？Positive effect的刻画并不困难，可以从其他方法得到，但是SDE对噪声和随机性的刻画具有天然的优势，更能说明线性近似假设的误差来源。

我们发现第一项中训练集的每个样本通过期望的方式加权，影响测试acc的增长速率，因此，我们定义sample effect，它表达每个样本在CE Loss下与梯度期望的内积：

可以将RL的学习速率（即飘移项）的近似用sample effect表示：

SFT蒸镏的最优目标分布

上一节得到的近似项对于SFT同样成立。RL是“从自身输出分布中学习”，只需将SFT看作“从一个未知分布中采样并学习”即可。我们考虑带有正确性过滤的蒸镏，有一个目标分布  ，采样并去除错误样本，可以看作从分布  采样，其中p(s)是每个问题s对应的正确概率，满足  ，这一设定和文中实验一致。 当我们只考虑飘移项第一项时，SFT的test acc增长速率可写为：

得到这两个近似有什么用？给定一个模型  和数据集，它的RL过程是固定的，我们想要找到最优的目标分布 ，使得SFT蒸镏的泛化性尽可能高于RL，并且研究这个最优分布的性质。为了得到有意义的结论，我们为最优分布满足的优化目标加上KL约束，最优分布  将最大化下列目标：

在附录A.2中，我们沿用DPO的思路证明了最优分布为：

其中Z(a,s)与样本正确性有关，hat r的定义是 

直观地，V越大，输出概率越高。具体来说，对任意两个正确答案a1和a2，它们在最优分布中的概率满足：

只要a1的sample effect大于a2，就能找到足够小的beta使得a1的生成概率大于a2. 这从理论上说明了提升SFT效率需要使用较高sample effect的样本训练。

引入KL约束还能带来一个奇妙的性质，如果我们改变每个问题的正确率p(s)，它在过滤后的最优分布  中总是和beta一起出现，因此改变p(s)等价于设定另一个beta，使得分布不变。这说明在正确性过滤后，target policy的accuracy并不重要。

RL如何改变输出样本的sample effect

高效SFT需要target policy生成较高的sample effect，人工构建数据集是一个简单的想法。但是有什么方法能找到这种policy？我们证明了RL能保证提升输出样本sample effect。

首先我们定义一个数据集上的sample effect期望，即dataset effect，它的定义基于一个base model  ，一个target policy  和数据集：  注意  经过正确性过滤后才是实际采样分布  。

我们研究target policy在RL过程中，输出dataset effect如何随之变化。在RL过程中  的初始值为  ，是一个随时间变化的随机矢量，在数据集和初值固定时，dataset effect是  的一个统计量，因此它也可用SDE求出飘移项，即dataset effect的增长速率。我们在附录A.3中证明了，在第一步迭代时，dataset effect的下界与acc增长速率有关。如果RL导致训练reward上升，那么dataset effect上升的速率至少是它的平方：

这种增长来自于正确性过滤吗？dataset effect定义在过滤后的分布上，因此它意味着过滤后的effect依然增长，而不是过滤本身带来的增长。

这种增长能从训练reward下降（负数的平方）产生吗？由于飘移项估计不考虑学习率、train batch size等现实误差，因此第一步优化导致的reward变化一定是非负的，不存在reward下降情况。

重蒸镏(Re-distillation)：仅用SFT复现RL

我们提出的重蒸镏方法的原理是：首先从Base model做小规模SFT得到SFTed model，再做RL得到target policy，从target policy中蒸镏小规模数据，重新训练Base Model得到Re-distilled model。重蒸镏的具体实现和SFT没有区别，这个名词只是表示它对模型的要求（从RL-trained模型蒸镏）。这个过程在理论上的解释也相对清晰：最大化SFT效率需要较高的sample effect，而RL可以提升sample effect，那么RL后的模型输出做SFT效率可能较高。它具体有多高？实际上，仅用不到1K例样本即可直接达到RL后的泛化性能。在产生显著提升的K&K数据集上也依然成立。

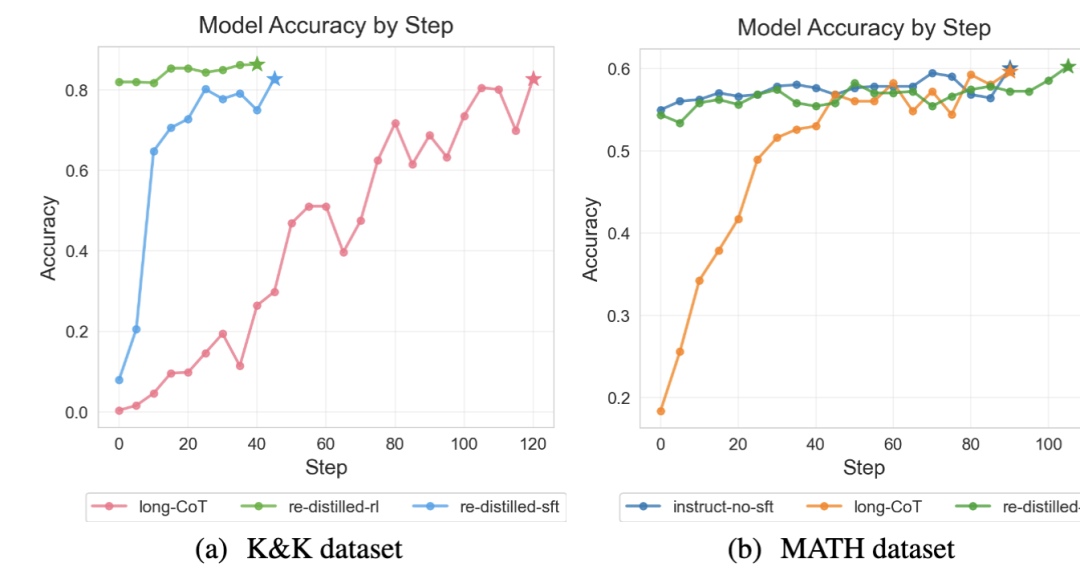
在K&K数据集上，我们做了两个重蒸镏实验，re-distilled-rl使用RL训练集蒸镏，确保Dt=De，re-distilled-sft使用SFTed model训练时的问题，N_ppl={2,3}，不满足De=Dt条件，但是可以和long-CoT公平比较。我们发现re-distilled-sft表现出5倍的效率提升，在25 step即可达到80%以上的test acc，而re-distilled-rl仅用SFT即可达到long-CoT训练125 step的性能。在MATH上，SFT数据集和RL训练集从同一个分布中分割，因此re-distilled-sft满足De=Dt条件，仅使用496例数据做重蒸镏，它的accuracy在SFT后与instruct极为接近，并且在之后表现出几乎一致的reward曲线。

假设验证：验证线性化假设的正确性

尽管重蒸镏实验与理论预测一致，但线性化假设的解释能力是否足够？数据集的实际sample effect是否完全不同？只考虑RL或SFT的第一步确实会引入误差，为了衡量这个误差的大小，我们用更贴近定义的方式计算不同数据集对应的acc增长速率，即  和  ，并将其和真实RL的性能曲线进行对比。

对于SFT，  越大，那么SFT后的test acc应当越高，这是一步能概括多步的假设。对于RL，  越大意味着初始reward增长速率越快。计算sample effect的公式是

然而，上述公式在实际应用时是存在问题的。因为

• • 实际优化采用Adam而非SGD，因此参数更新量并不对应梯度；
• • RL采用的是GRPO而不是简化的REINFORCE。

我们的核心目的是验证“用单步+线性假设计算的effect可以有效估计多步非线性的效果”，只要保持单步+线性条件不变，其他设置应当尽可能接近实际训练，因此在计算时做了如下设定：

• • 同时计算SGD和Adam对应的sample effect，Adam受到历史梯度影响，设置SFT的batch size为1，RL的batch size为20，这是因为RL下batch size对grad clip和adv=0样本的影响不可忽略，而实际SFT和RL的batch size比例为64:1024也大致符合1:20的比例
• • 引入实际训练存在的gradient clip和计算RL所需的GRPO loss，advantage用原始replay buffer的数据计算
• • 计算V所需的测试集梯度期望非常重要，由于每个模型的这一项不同，无法公平比较。我们统一采用Qwen2.5-1.5B base直接做RL在25 step得到的checkpoint与原base model的参数差值的方向矢量作为梯度。这一方向能确保是有效的，因为25 step时test acc已经产生了显著上升，并且不受到SFT影响。
• • 我们测试instruct, long-CoT, short-CoT在上述base model梯度方向下的sample effect，避免自己测自己产生的bias

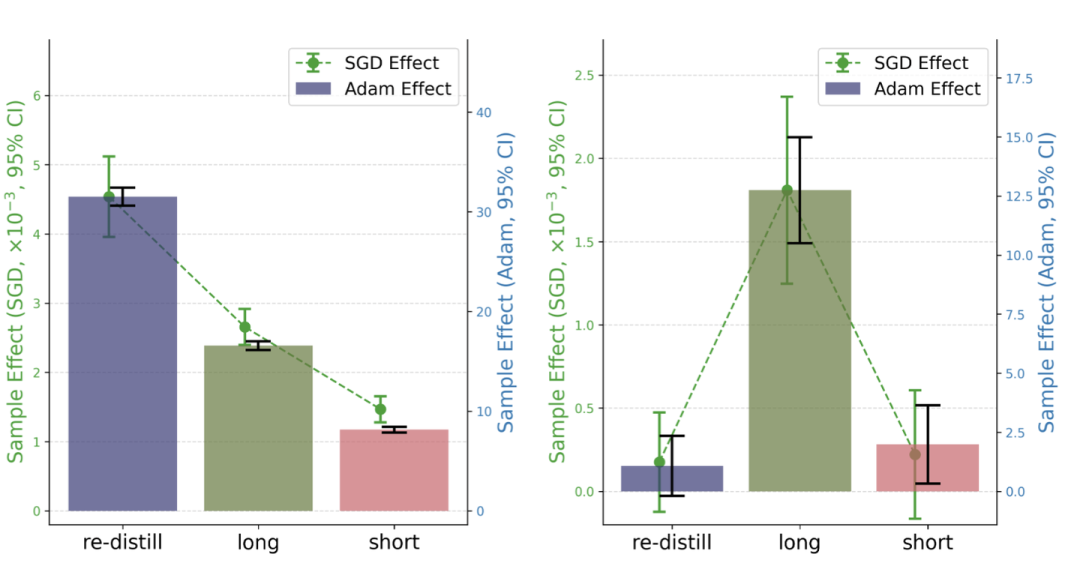
左图是SFT下计算的reward增长速率，Adam和SGD测试趋势一致。其中re-distill效果最好，这与实际SFT效果相符，long-CoT和short-CoT的相对大小与实际观测相反，这可能是因为long-CoT相比short-CoT的token更多，需要更多样本才能降低噪声，而我们没有考虑噪声的影响。右图是RL下计算的reward增长速率，long>short>re-distill，这与实际观测结果相符。re-distill较低是因为它在一开始已经收敛了，所以增长速率很低。

我们在线性化假设下计算的sample effect与真实训练结果趋势相符，仅long和short顺序不一致。这说明即使只看第一步也能对多步非线性优化效果有一个相对准确的估计，佐证了理论对重蒸镏的指导作用。

RL的探索困境：为什么SFT能改变long-term exploration

小规模SFT改变RL的初始探索模式并不反常，然而，随着RL进行，policy应当能探索到不同的思维模式，但实际表现却是RL很难跳出SFT给定的思维模式（例如R1中的Okay、Wait等字样）这是为什么？上述理论仅适用于step不多的情况，因此我们从自回归的角度来解释long-term effect of SFT。

直觉上，LLM的自回归生成决定了初始token和靠后的token受到随机性的影响不同。当靠后的token没有收敛到较好的状态时，初始token无法得到有效的advantage。例如模型总是在100 token后生成乱码，初始token的advantage都是0，模式不会改变。

我们观察long-CoT-math的RL replay buffer，记录每个token在initial policy上的logprob，并按照token在response中的位置计算最低1%分位数。例如，取所有response的第二个token，计算1%分位数作为position=2的logprob。如果这个值随着RL过程下降了，说明输出模式在该position发生了改变，即信息从后向前传递到了这个位置。

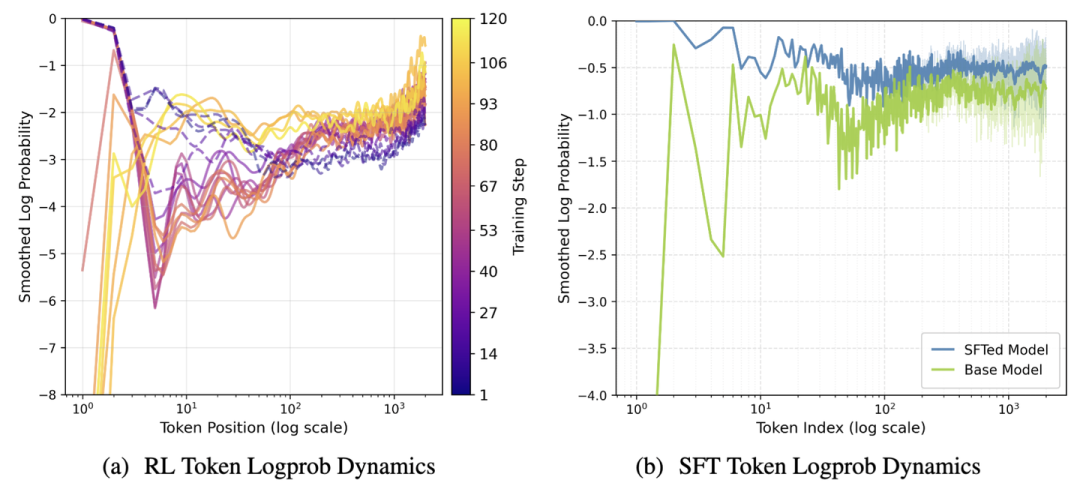
测试结果如上图所示，左图表现出非常有意思的曲线：随着RL进行，曲线颜色由深变浅，logprob最低的位置逐渐向前转移。而policy收敛时靠后的token logprob竟然升高了。这说明RL表现出了从后向前的模式转变：靠后的token优先被改变，而靠前的token最后改变。但是SFT的趋势则相反，右图显示SFT前后的logprob变化，靠前的token反而是提升最多的。这说明了RL和SFT的互补关系，如果我们对探索的先验有一定认识，通过SFT修改靠前的token分布将远优于通过RL自主探索。LLM RL的探索与经典RL的不同也可以从这里看出，LLM的探索更需要依靠小规模SFT这一工具，而非通过随机性遍历状态空间。

总结与讨论

这篇文章其实只覆盖了原文中的主要部分。更多有趣的现象没有提到，例如Re-distillation中CE loss在一个epoch内下降到接近0的水平、MATH数据集上表现出的test acc撞墙现象、提升temp的影响、hyper fitting和更大规模SFT的影响等等。

我们也希望这篇文章对于理解RL的瓶颈有所帮助，RL是否是独立于参数以外的scaling law还需要进一步验证，我们证明了RL过程的计算量远超实际修改模型参数所需的计算量，说明RL带来的提升并非通过大规模修改原模型的内在结构实现。线性化假设并没有得到完美验证，说明在SFT情景下，distribution shift也可能有重要作用，未来研究可以改进这一假设并给出更合适的估计手段。

最后，我们提出的方法是post-hoc方法，并没有避免第一次RL的计算量。尽管重蒸镏可以用于base model而非严格地限制为initial policy，将post-hoc方法改为真正能work的方法是很有吸引力的。这一方向也有很大困难，因为改进post-hoc意味着凭空节省算力，但至少使用early checkpoint筛选原始数据集中缺陷较大的样本是可能的。