翁荔最新万字长文：Why We Think

金磊 发自 凹非寺
量子位 | 公众号 QbitAI

《Why We Think》。

这就是北大校友、前OpenAI华人VP翁荔所发布的最新万字长文——

围绕“测试时计算”（Test-time Compute）和“思维链”（Chain-of-Thought，CoT），讨论了如何通过这些技术显著提升模型性能。

翁荔表示：

让模型在输出答案前多思考一会儿（比如通过智能解码、思维链推理、潜在思考等方法），能显著提升它的智能水平，突破当前的能力瓶颈。

网友们看罢，纷纷打出了“精彩”二字：

感觉就像打开了人工智能理解的一个全新维度。

那么接下来，我们就来深入了解一下这篇文章。

动机

让模型思考更长的时间可以通过几种不同的方式来激发。

心理学类比

核心思想与人类思考方式深度关联。

人类无法立即回答“12345×56789等于多少？”，而是需要时间分析——这正是Daniel Kahneman在《思考，快与慢》（2013）中提出的双系统理论：

• 快速思考（系统1）：直觉驱动，快速自动但容易出错
• 慢速思考（系统2）：逻辑性强，需刻意调动认知资源

因为系统1思维是快速和简单的，它经常以准确性和逻辑性为代价，成为主要的决策驱动因素。它自然依赖于我们大脑的思维捷径（即启发式），并可能导致错误和偏见。

通过有意识地放慢速度，花更多的时间来反思、改进和分析，我们可以进入系统2思考，挑战我们的本能，做出更理性的选择。

作为资源的计算

深度学习的一种观点是，神经网络的特征是它们可以通过向前传递访问的计算量和存储量，如果我们优化它们来使用梯度下降来解决问题，优化过程将找出如何使用这些资源——它们将找出如何将这些资源组织成计算和信息存储的电路。

从这个角度来看，如果我们设计了一个架构或系统，可以在测试时进行更多的计算，并且我们训练它有效地使用这些资源，那么它将工作得更好。

在Transformer模型中，模型为每个生成的令牌所做的计算量（flops）大约是参数数量的2倍。对于像混合专家（MoE）这样的稀疏模型，每次前向传递中只使用一小部分参数，因此计算量= 2 *参数/稀疏度，其中稀疏度是活跃专家的比例。

另一方面，CoT使模型能够为它试图计算的答案的每个令牌执行更多的计算。事实上，CoT有一个很好的特性，它允许模型根据问题的难度使用可变的计算量。

潜变量建模

经典机器学习方法通过潜变量z和可见变量y构建概率模型，其中y是给定观测值。通过边缘化（求和）潜变量可表达可见变量的丰富分布：

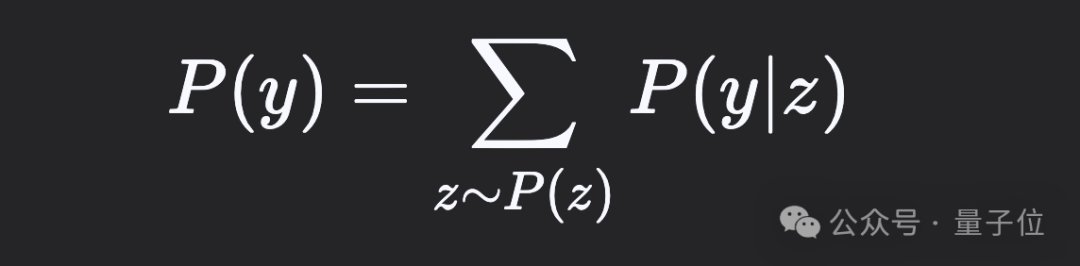
例如，用x表示数学题目，y为正确答案，z为推导过程，则需优化的边缘概率为：

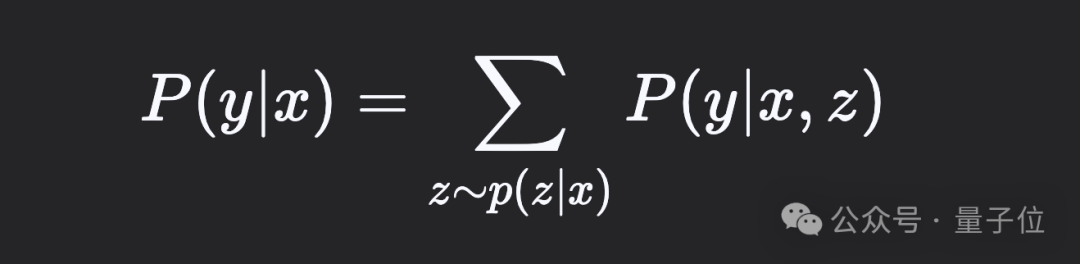
该视角尤其有助于理解多并行CoT采样或搜索算法——这些可视为从后验分布P(z∣x,y)P(z∣x,y)中采样。同时表明应优化对数损失log⁡P(y∣x)logP(y∣x)，因其在预训练中效果显著。

基于Token的思考

Ling等（2017）在AQUA-RAT数据集中首次探索为数学问题生成中间步骤，后由Cobbe等（2021）在GSM数据集扩展。

他们通过监督学习训练生成器（基于人工解题步骤）和验证器（判断答案正确性）。Nye等（2021）实验性使用“草稿纸”式中间token，Wei等（2022）则提出标准术语思维链（CoT）。

早期改进CoT的方法包括：

• 对人工书写推理轨迹进行监督学习
• 筛选模型生成的正确答案轨迹（可视为强化学习的雏形）
  另有研究发现，通过适当提示（如”逐步思考”或引导模型先关联知识）能显著提升指令微调模型的数学能力。

后续研究表明，在可自动验证答案的数据集（如STEM题目或带单元测试的编程题）上应用强化学习，可大幅改进CoT推理能力。

这一方法因DeepSeek-AI（2025）发布的R1技术报告而受到关注，该报告显示简单的策略梯度算法即可实现强劲性能。

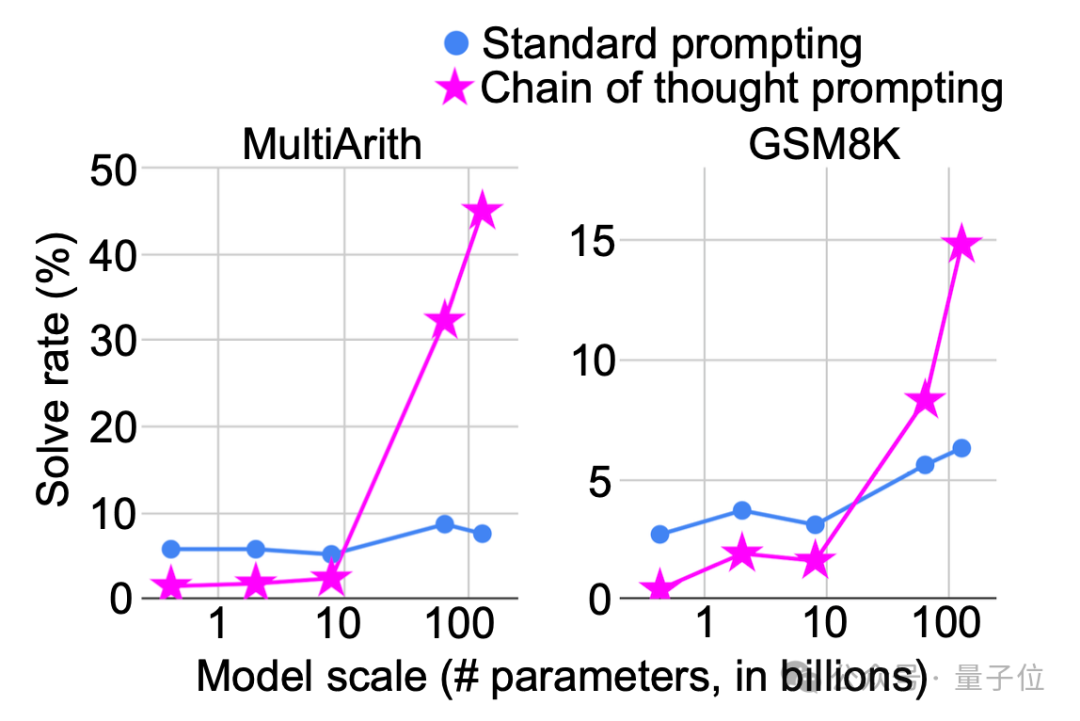
△思维链提示提高数学问题求解成功率。模型越大，思考时间收益越显著。

分支与编辑

测试时计算的根本目的是自适应修改模型在推理时的输出分布。主要方法包括：

• 并行采样：同时生成多个输出，通过过程奖励或验证器筛选。如N选1或束搜索。自洽性（Wang等，2023）常用于无真实答案时对多CoT结果投票。
• 顺序修订：基于上一步输出迭代修正，需依赖微调模型——单纯依赖模型自校正能力可能导致性能下降（Huang等，2024）。

并行采样方法简单、直观、易于实现，但受其能否一次性得到正确解的模型能力的限制。

序列明确要求模型对错误进行反思，但它的速度较慢，在执行过程中需要格外小心，因为它确实存在正确预测被修改为不正确或引入其他类型幻觉的风险。

这两种方法可以一起使用。Snell等人（2024）表明，简单的问题受益于纯粹的顺序测试时间计算，而较难的问题通常在顺序与并行计算的最佳比例下表现最佳。

△并行采样与顺序修订的图解。

并行采样

给定一个生成模型和可用于评估完整或部分样本的评分函数，我们可以采用多种搜索算法来寻找高分样本。

其中最简单的算法是N选一（Best-of-N）：只需收集N个独立样本，然后根据评分函数选择排名最高的样本。

而束搜索（Beam search）是一种更复杂的搜索算法，它能自适应地分配更多计算资源到解空间中更有潜力的区域，从而优化搜索过程。

束搜索通过维护一组有潜力的部分序列，交替执行以下操作：

1. 扩展：对候选序列进行延续生成
2. 剪枝：淘汰潜力较低的序列

作为选择机制，我们可以采用过程奖励模型（PRM；Lightman等人，2023）来指导束搜索的候选选择。

Xie等人（2023）的创新方法在于：让大语言模型以选择题形式自我评估其生成推理步骤的正确性，研究发现这种逐步骤自评机制能有效减少束搜索解码过程中多步推理的误差累积。

此外，在采样过程中采用退火温度调节有助于降低随机性带来的影响。基于Codex模型的实验表明，该方法在GSM8k、AQuA和StrategyQA等小样本基准测试中实现了5-6%的性能提升。

Wu等人（2025）提出的奖励平衡搜索（REBASE）通过独立训练PRM模型，根据softmax归一化的奖励分数，动态决定束搜索过程中每个节点在不同深度的扩展程度。

Jiang等人（2024）开发的RATIONALYST系统则专注于：基于海量无标注数据合成推理依据，并通过以下标准筛选优质依据：

当推理依据被纳入上下文时，真实答案token的负对数概率是否显著降低（通过阈值判断）。

在推理阶段，RATIONALYST通过两种方式为思维链生成器提供过程监督：

1. 隐式指导：帮助估计后续推理步骤的对数概率
2. 显式指导：直接作为提示部分生成后续推理步骤

有趣的是，即使没有明确的零样本或少样本提示，也能激发出思维链推理路径。

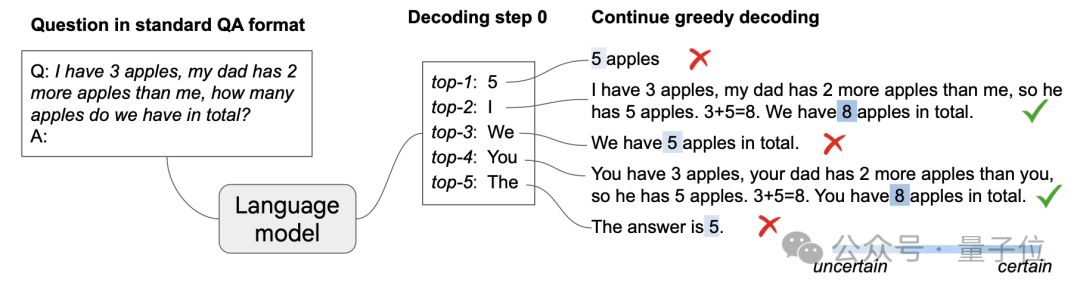
Wang和Zhou（2024）研究发现：如果在第一个采样token处保留置信度最高的前k个候选（这个置信度是通过采样时top-1和top-2候选之间的差值来衡量的），然后用贪婪解码继续这些采样尝试，很多情况下模型会自动产生思维链。

特别当上下文里确实出现思维链时，最终答案的解码置信度会明显更高。要计算最终答案的置信度，需要通过任务特定的启发式方法（比如数学题取最后一个数字）或者用”所以答案是”这样的提示来定位答案范围。

这个设计之所以选择只在第一个token处分支，是因为研究发现：早期分支能大幅增加潜在路径的多样性，而后续token会受到前面序列的很大影响。

顺序修订

若模型能够反思并修正先前响应中的错误，理论上应能生成质量逐步提升的迭代修正序列。

然而研究表明，大型语言模型（LLMs）本质上并不具备这种自我修正能力，且直接应用时易出现多种故障模式，包括：

1. 幻觉现象，即将正确响应修改为错误；
2. 行为坍缩至非修正状态，例如对初始错误响应仅作微小改动或完全不修改；
3. 无法适应测试时的分布偏移。Huang等人（2024）的实验证实，简单应用自我修正会导致性能下降，必须依赖外部反馈机制才能实现有效改进。

这些反馈可基于以下要素：真实答案匹配、启发式规则与任务特定指标、编程问题的单元测试结果（Shinn等，2023）、更强模型的指导（Zhang等，2024），以及人类反馈（Liu等，2023）。

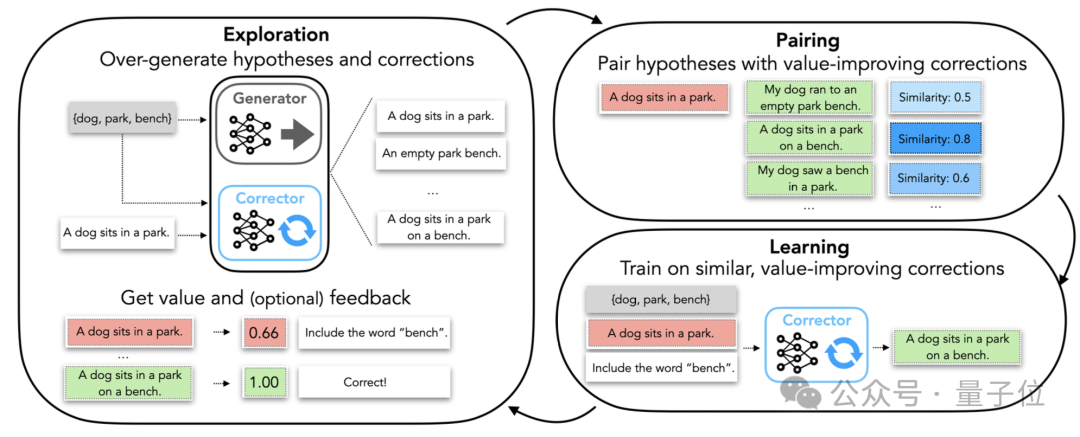
自我修正学习（韦莱克等人，2023 年）旨在给定一个固定的生成模型P0(y0∣x)的情况下，训练一个修正模型 Pθ(y∣y0,x)Pθ(y∣y0,x)。生成模型保持通用性，而修正模型可以是特定于任务的，并且仅在初始模型回复和额外反馈（例如一句话、编译器跟踪信息、单元测试结果；反馈可以是可选的）的条件下进行生成：

1. 自我修正学习首先针对数据集中的每个提示生成多个输出；
2. 然后，如果对于同一提示的两个输出中，一个比另一个具有更高的值，就将它们配对，形成价值提升对（提示x，假设y，修正y’；
3. 这些配对根据价值提升量v(y′)−v(y)v(y′)−v(y)以及两个输出之间的相似度Similarity(y,y′)(y,y′)按比例选取，用于训练修正模型；
4. 为了鼓励探索，修正模型也会向数据集中提供新的生成结果。在推理阶段，修正模型可以迭代使用，以创建顺序修正的轨迹。

Qu等人（2024）提出的递归式审查方法同样致力于训练更优的修正模型，但其创新之处在于采用单一模型同时承担生成与自我修正双重功能。

Kumar等人（2024）开发的SCoRe（Self-Correction via Reinforcement Learning）采用多轮次强化学习策略，通过激励模型在第二次尝试时生成优于首次尝试的答案来实现自我修正。该框架包含两个训练阶段：

1. 第一阶段：仅优化第二次尝试的准确率，同时对第一次尝试施加KL散度惩罚项，以防止初始响应过度偏离基础模型行为特征；
2. 第二阶段：联合优化第一次和第二次尝试的响应准确率。

理论上，我们期望两个阶段的响应质量都能得到提升。第一阶段的设计有效规避了模型对初始响应仅作微小修改或完全不修正的”行为坍缩”现象，而第二阶段的实施则进一步提升了整体修正效果。

由于原博客过长，后续的内容仅概括展示大致内容；想要深入了解，可以查看文末的原文链接。

强化学习与外部工具整合

RL for推理：

• DeepSeek-R1：通过SFT-RL训练（含格式奖励与准确率奖励），在MATH-500等基准上性能接近OpenAI o1-preview。
• 纯RL的涌现能力：无需SFT阶段，模型通过RL自然学会反思与回溯（“aha moment”）。

外部工具：

• 代码执行：PAL/Chain of Code将数学计算offload至代码解释器，避免模型学习底层计算。
• 知识搜索：ReAct结合Wikipedia API，在HotpotQA等任务中引入外部知识。

思维忠实性与优化压力

忠实性验证：

• 实验发现：CoT可能存在 “早期结论”“无信息标记” 等问题，Lanham实验显示仅约60%模型在多选择题中依赖真实推理。
• 影响因素：奖励模型（RM）可能降低忠实性，而推理模型因优化最终答案更倾向忠实表达。

奖励破解风险：

• 直接优化CoT监控信号可能导致模型隐藏破解行为（Baker et al. 2025），如用重复文本绕过长度奖励约束（Yeo et al. 2025）。

连续空间思维与架构创新

循环架构：

• Universal Transformer：结合自注意力与循环机制，动态调整计算步数。
• Geiping递归块：在Transformer顶部添加循环层，通过随机状态迭代优化推理，实验显示3.5B模型在r=32步时性能饱和。

思维标记技术：

• 显式标记：插入或暂停标记（如 <#>）增加计算时间，Goyal 实验中数学题准确率提升显著。
• 隐式标记：Quiet-STaR在每个token后生成推理标记，零 – shot 下GSM8K成功率从5.9%提升至10.9%。

缩放规律与未来方向

计算效率：

• 测试时计算与模型规模互补，小模型 + 高级解码算法可实现成本 – 性能最优（Snell et al. 2024）。
• 强制延长思维链（如追加 “wait”）与准确率正相关，但拒绝采样可能导致负向缩放。

未来挑战：

• 如何在 RL 中激励人类可读的忠实推理？
• 无监督场景下的自我修正机制如何设计？
• 如何将测试时性能提升迁移至基础模型（如蒸馏）？

（文：量子位）