
©PaperWeekly 原创· 作者 | 王群中
单位 | 香港中文大学本科生
研究方向 | 数据挖掘

导读
近年来,随着图神经网络(Graph Neural Networks, GNN)在推荐系统、生物信息、社交网络等领域的广泛应用,“图提示”(Graph Prompting)作为一种轻量级迁移学习方法逐渐受到关注。
该方法通过对输入图结构进行微调(如添加提示向量或子图),在不修改模型参数的前提下适配新的任务场景,显著简化了模型部署流程。过去三年内已经有几十篇相关研究出现,在推荐系统、药物发现、社交网络等多个领域频频出圈,成为图神经网络的新宠。
尽管已有多项实证研究表明图提示具有良好性能,但该机制的理论基础尚不明晰。理论性的缺乏使得过去基于经验的图提示研究工作频频遭受质疑,成为图提示研究的一朵令人不安的“乌云”。
为回应这一研究空白,香港中文大学王群中(大二本科生)、孙相国博士(共同一作、通讯作者)、以及程鸿教授,近期在 ICML 2025 的论文 “Does Graph Prompt Work? A Data Operation Perspective with Theoretical Analysis”,系统提出从“数据操作”视角理解图提示的理论框架,从数学上系统解释了图提示的工作机制,并给出了形式化定义、误差上界分析及分布刻画,为图提示的有效性提供了明确的理论支撑。

论文名称:
Does Graph Prompt Work? A Data Operation Perspective with Theoretical Analysis
论文链接:
https://arxiv.org/abs/2410.01635
代码链接:
https://github.com/sheldonresearch/ProG

原来图提示是在“改图”,而不是“改模型”
传统做法是:先预训练一个模型,再针对新任务微调模型参数。这过程复杂又耗时,像是在反复“拆机换件”。图提示则完全不同——它保留原模型不动,只在输入的图数据上“加点料”,例如加上几个特殊节点或特征向量,让原模型自己“看懂”新任务。
已有研究指出,这种机制在实际中可能等价于某种图数据操作(如添加节点、修改特征、删除子图等)。但这些结论大多基于实验观察,缺乏系统化的理论分析。这篇论文试图以形式化的方式回答两个核心问题:
-
图提示是否具备模拟图数据操作的能力?
-
这种能力是否能够稳定地转化为下游任务性能提升?

图提示为何有效?从数据层面看图提示机理
该论文最重要的理论贡献是提出了一个关键概念:“桥接图”(Bridge Graph)。
简单说,就是对于每一个原始图数据,都可以通过某种“数据操作”变成一个新的图,这个新图经过原来的预训练模型处理后,结果就能“神奇地”符合下游任务要求。而图提示,就是学会如何找到这个数据操作,并在理论上证明了:
-
这样的“桥接图”确实存在;
-
误差是可控的,而且通常很小;
-
不管是处理一个图,还是一批图,都能有效运作;
-
即便模型结构很复杂(比如用了注意力机制),理论也依然成立。
这等于从根上说明:图提示不是“偶然有效”,而是“必然有效”!

研究贡献一:提出“桥接图”理论,刻画图提示的本质能力
作者引入“桥接图”(Bridge Graph)和 “ε – 扩展桥接集”等概念,形式化描述图提示如何在理论上将原始图转换为可被预训练模型正确解析的图嵌入。这一转化等价于找到某种图操作函数,使得模型输出近似等同于下游任务的最优结果。
论文证明了如下结论:对任意下游任务和输入图,始终存在一组提示结构,可以使得图提示生成的图嵌入接近目标嵌入函数输出,且该误差具备上界。


研究贡献二:推导误差上界,并刻画误差来源与可控性
论文进一步从模型结构角度推导了图提示误差的理论上界,并分析了误差的来源及可控因素。主要结论包括:
-
在 GNN 的权重矩阵为行满秩时,可以在理论上实现无误差匹配;
-
在非满秩情况下,误差的上界可由模型秩缺失度(如矩阵秩损失)与数据复杂度共同决定;
-
对于多个图组成的数据集,误差的均方根值仍可被一个全局上界控制,该上界与下游嵌入矩阵的主成分谱有关;
-
提示结构的复杂度(如提示向量个数)与误差控制能力成正相关,但其增长速度可远低于样本数量的增长,提示学习具备良好的可扩展性。
这些推导结果为后续设计提示结构提供了理论指导,支持当前实证中“中等规模提示即可取得良好效果”的经验观察。

研究贡献三:误差的统计分布建模及对非线性模型的扩展
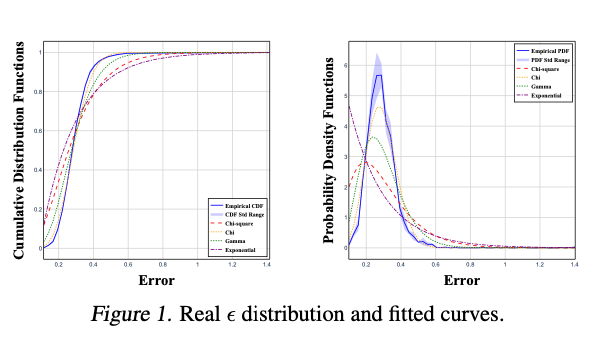
除了分析误差上界,作者还尝试刻画误差的数值分布形态。通过理论分析与模拟实验,发现当提示参数被合理优化后,残差误差在一定假设下近似服从卡方分布(Chi distribution),其自由度与模型秩损失相关。
此外,论文还将理论框架扩展至包含非线性结构的 GNN 模型(如 GAT),证明在具有足够表示能力(如权重矩阵满秩)的条件下,上述图提示能力仍然成立,增强了该理论的适用范围。

实验验证:理论与实践相符
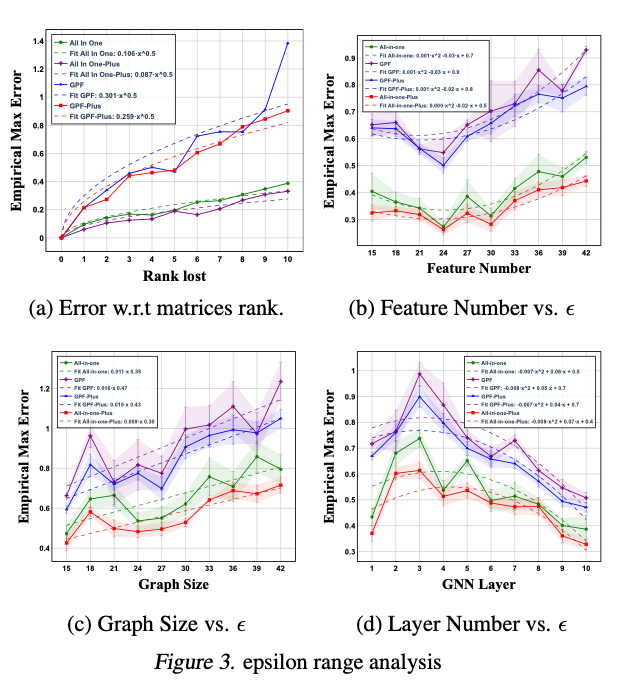
为验证理论结果,作者在合成图数据和真实图数据上开展了广泛实验,包括不同模型结构(GCN/GAT)、不同提示策略(GPF/All-in-One)和不同数据规模等设置。主要实验观察包括:
-
在满秩条件下提示学习可达到接近零误差;
-
在非满秩情况下,误差表现与模型表示能力和提示规模一致;
-
随着提示复杂度适度提升,误差迅速下降并趋于收敛;
-
多图任务中,提示规模的需求随样本增长速度显著低于线性趋势。

总结
研究首次从理论角度系统剖析图提示机制的本质,并对其有效性给出严谨的数学证明。通过引入桥接图、误差上界分析、分布建模等理论分析,论文为图提示从工程技巧走向可解释建模提供了坚实基础。
未来,该理论框架可为图提示方法的结构设计、复杂度控制与泛化分析提供参考,也有望推动图神经网络在跨任务、跨域、低资源等复杂场景下的进一步发展。关于图提示的更多
(文:PaperWeekly)

