









 是否是 (1) 的解。在一维情况下,S_t 定义微分同胚( diffeomorphism),因此
是否是 (1) 的解。在一维情况下,S_t 定义微分同胚( diffeomorphism),因此 是单调的,
是单调的, 也是单调的。因此,它是凸函数的梯度,根据 Brenier 定理使其最优。如果 β 是高斯分布,直到空间旋转以使协方差对角化,则扩散映射由沿每个轴的单调映射定义,并且也是最优传输。
也是单调的。因此,它是凸函数的梯度,根据 Brenier 定理使其最优。如果 β 是高斯分布,直到空间旋转以使协方差对角化,则扩散映射由沿每个轴的单调映射定义,并且也是最优传输。
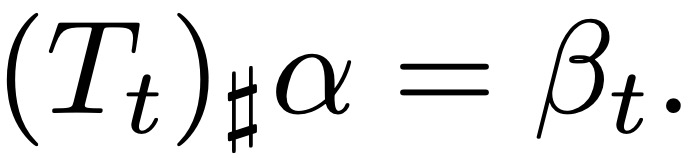 目标是证明:如果 β 选择得当(具体来说,非常接近 α,且特定的二阶和四阶对数密度导数为 0),那么 T_t 是所有 t 的最优传输会导致矛盾。根据 Brenier 定理,T_t 是最优传输意味着它是凸函数的梯度,这相当于:
目标是证明:如果 β 选择得当(具体来说,非常接近 α,且特定的二阶和四阶对数密度导数为 0),那么 T_t 是所有 t 的最优传输会导致矛盾。根据 Brenier 定理,T_t 是最优传输意味着它是凸函数的梯度,这相当于:
-
对 (7) 对 t 求微分
-
对流 ODE (4) 对 x 求微分

 则 (8) 意味着:
则 (8) 意味着:
 并且 T 和 S 是逆最优传输映射,因此将
并且 T 和 S 是逆最优传输映射,因此将 表示为 ψ 凸。Monge-Amp`ere 方程 (2) 意味着:
表示为 ψ 凸。Monge-Amp`ere 方程 (2) 意味着:


 和
和 不能交换。在 0 附近,h 必须至少是 4 次多项式。二维情况下的一个示例是:
不能交换。在 0 附近,h 必须至少是 4 次多项式。二维情况下的一个示例是:

2024亚马逊云科技 re:lnvent 《拉斯维加斯有约》直击现场——Matt Garman & Peter Desantis 主题演讲中文解读
了解亚马逊云科技独树一帜的创新实践与文化和全系列前沿解决方案、如何开拓创新并引领全球云计算的全方位发展、如何重构基础架构并打造全新体验,探索如何依托强大的数据基础为客户打造创新的、差异化的解决方案。
聆听客户发言人分享真实案例,了解如何利用数据支持包括生成式 AI 在内的各种应用场景,进而打造独一无二的客户体验。
分享亚马逊云科技及其合作伙伴为客户带来的积极变革,赋能其重塑商业模式、取得非凡成就。
这不仅是一场深入了解前沿技术、数据应用和创新实践的盛会,更是一个不容错过的交流平台。期待您的加入!

©
(文:机器之心)

