DualPipe深入浅出：没有分布式训练基础也能看懂的DualPipe全方位讲解

©PaperWeekly 原创 · 作者 | 张逸骅

单位 | 密歇根州立大学博士生

研究方向 | 可信人工智能

引言

1.1 单卡时代：从手工小作坊说起

1.2 模型并行（Model Parallelism）：工艺手册的拆分艺术

1.3 数据并行 （Data Parallelism）：克隆车间计划

1.4 张量并行（Tensor Parallelism）：协作加工超大单件

1.5 流水线并行（Pipeline Parallelization）：让不同机床同时高效运转

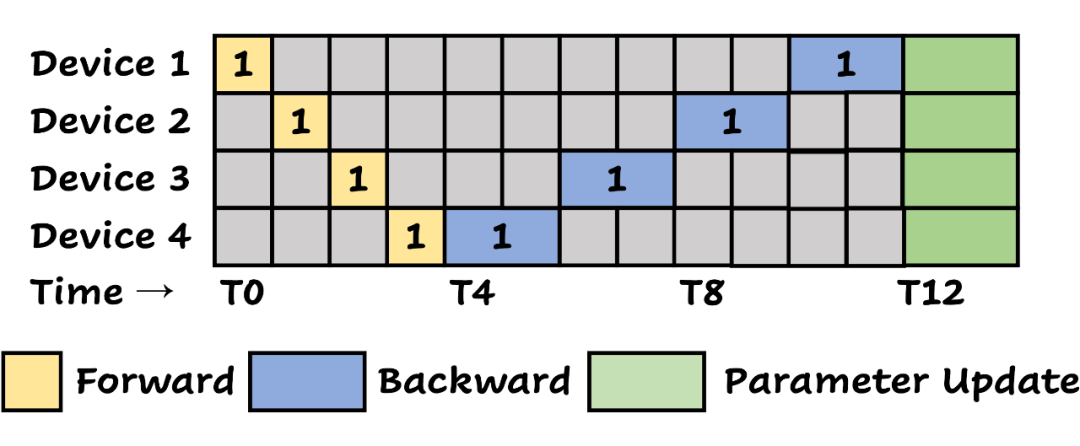
▲ 不采用流水线并行时，数据的传输流程：数据在模型的不同部位依次传递，每次只有一个 GPU 在工作，大量的等待时间使得 GPU 的利用效率非常低。

▲ 1F1B 流水线并行方案示意图

1.6 当流水线依然有“死角”：ZB1P 的局限性

双管齐下的流水线调度：DualPipe

2.1 双向调度（Bidirectional Scheduling）：把“前后”同时推上生产线

其中， 表示流水线的深度，即参与计算的阶段数； 和  分别代表前向与后向计算所需的时间，而  则是激活数据累积的窗口大小。

通过对比三个方法，我们发现：

• 1F1B 方法：这种最基础的单向流水线调度方式，其气泡数量为 。也就是说，每个阶段在前向和后向之间都有固定的等待时间，整个流水线几乎是严格串行的。激活数据则为 ，说明每个流水线阶段仅需存储一份激活数据。

• ZB1P 方法：通过将后向传播的部分计算（例如输入梯度与权重梯度的拆分）解耦，ZB1P 成功减少了气泡数量，将其降低到 。不过，激活数据的需求并未改变，仍然是 。

• DualPipe 方法：DualPipe 采用双向流水线和计算与通信重叠的策略，将前向和后向同时注入流水线，从而大幅度降低了流水线中的空闲等待（气泡）。表中显示，其气泡数量为 。可以看到，相较于传统方法，气泡数明显减少，但为实现这种重叠调度，激活数据的存储需求相应提升到了 。

通过这个表格，我们可以直观地看到 DualPipe 在调度上所作的优化：

• 气泡减少：双向调度和通信重叠使得前向和后向可以并行进行，从而减少了等待时间；
• 激活数据增加：为了支持这种高效的重叠机制，需要在每个 GPU 上额外保留一份激活数据，从而使得激活存储量比传统方案略有增加。换句话说，DualPipe 是在“牺牲”少量显存的前提下，极大地提高了流水线的利用率，使得 GPU 在大规模分布式训练中能以更高的吞吐率持续运转。这正如老王在车间里通过引入双向运输系统，不仅提高了机床的利用率，还确保了在高负载下依然能保持稳定高效的生产。

2.2 GPU 里的“计算-通信”交错：实现“边运边算”

• 在运送的那段时间里，锻造机床一直处于无事可做（idle）的状态；
• 铸造机床送完这 1000 个零件后，还要额外等待一下，看看锻造机床是否能及时消化完；

• 如果锻造机床处理速度比运输速度快或慢，两边都容易形成 “你等我、我等你” 的浪费。

分段运输的思路：若把这 1000 个零件拆成 4 次或 10 次小批量运输，只要第一批货物到达锻造机床，这台机床马上就能动工对前几百个零件进行锻造；与此同时，铸造机床（或搬运车）可以继续把第二批、第三批、第四批材料在后台运过来。

• 对锻造机床来说，它不用等所有材料都送达才能开工；它开始锻造第一批的同时，后几批尚在运输。
• 搬运车（通信）也不需要等待锻造机床“空出来”再去送下一批，而是能根据状态继续分段运输。

• 等到锻造机床处理完第一批零件之际，第二批零件可能也刚好运达，机床可以紧接着锻造第二批，如此交替推进，几乎没有空闲。

把这个思路放到 GPU（尤其是多 GPU、跨节点）环境下，具体会涉及几点：

1. 在计算和通信之间进行资源划分 GPU 有多个 SM（Streaming Multiprocessors）。当我们做大规模 all-to-all 或者 pipeline 传输时，可以让部分 SM 负责发包/收包（通信），另一些 SM 或流（Stream）负责进行前向或后向计算。

只要通信包不是太大，或者被拆分成较多小包，那些专门负责计算的 SM 就可以在“通信流”干活时依然执行算子，不用整块阻塞。

2. 数据按微批次或更小块切割：比如有一个模型的若干个层的特征张量需要传输，DualPipe 并不会一次性把这几个层全部发完再进行算子计算，而是分成若干小块（如甚至拆分到某个 attention 模块这种粒度）。

GPU 只要收到第一小块数据，就可以在计算流中先启动一部分前向或后向运算。这样就像“先送两箱货，机床马上开工；后面继续分批往下送”。

3. 通信与计算的并行调度：在 PyTorch 里，cuda 提供多流（multi-stream）异步执行：发起通信（P2P ops, all-to-all ops）后，程序无需立刻 wait()，可以让计算流直接开始干别的活。

只有在真的需要用到通信结果的那一刻，才去等待对应的事件。就像老王给搬运车下达运输命令（异步通信）之后，机床就去干别的事情，直到下一批材料实际用得到的时候，才会等待搬运车把货送达。

这就是“在运输过程中穿插加工计算”的本质：发起运输命令后，立刻让 GPU 去计算之前已经到达的那部分数据，而不是卡在那边干等传输结束。

4. 流水线机制：考虑到上边提到的 DualPipe 额外加入的双向流水线的思路，让当前 GPU 既能等待来自“前面的输出”，也能把后向的梯度送往“前面的 GPU”。在宏观调度上，多个微批次与多个 GPU 形成一个环环相扣的管线，一边发送数据，一边接受下一部分数据，并行执行。

最终，我们把“整块”的通信和计算分解成多次小规模的交替操作。从时间线上来看，通信和计算往往呈下列交叉图案：

时间轴:  ==================================>
通信流:   [comm chunk1]  [comm chunk2]   ...
计算流:         [compute chunk1]   [compute chunk2]  ...

• 当  comm chunk2  开始发送时， compute chunk1  可能已经在算前向/后向了；

• 当  compute chunk2  需要数据时， comm chunk2  大概率已快传完了；

• 双方就像齿轮一样咬合，不会出现长时间空转。

如果是大块整体传输，则类似：

(整块通信) [comm all data]  (等待结束) -> [compute all data]

• 计算必须等通信完全结束才能开始，通信完成后又可能很快结束，导致通信通道闲置；

• 期间 GPU 做不了别的事情——浪费了大量潜在计算时间。

源码如何实现“双管齐下”：DualPipe 关键逻辑解析

在上一个章节里，我们用机械加工的类比方式，说明了 DualPipe 如何让前向（Forward）和后向（Backward）真正地在同一个流水线上“同时上阵”，以最大化地利用 GPU 资源。

下面，我们来看看 DualPipe 的核心源码如何将这一思路落到实处，并通过拆分批次、管理通信、以及巧妙调用“前向-后向”协同来实现高度的重叠和极小化的流水线气泡。

3.1 类的基本结构与初始化

class DualPipe(nn.Module):
    def __init__(
        self,
        modules: Tuple[nn.Module, nn.Module],
        ...
    ) -> None:
        super().__init__()
        
        ...
        self.module = nn.ModuleList(modules)
        self.overlaped_forward_backward = ...
        ...

• modules：这里传入的是两个 nn.Module 的元组，通常代表流水线的“前半段”和“后半段”。想象一下，在机械加工的流水线里，这可能对应“前向加工”的组合机床（如铸造+锻造）和“后向调整”的另一个组合机床（如质量检测+参数调整）。

• overlaped_forward_backward：用于判断这两个 Module 是否支持前后向重叠的专用函数。只有当传入的 Module 有 overlaped_forward_backward 这个方法（且类型相同），才会在后续流程里真正地进行前后向同一批次的紧密交织。

与此同时，代码中还设置了一系列与分布式训练流程相关的参数和标记，如：

• self.group 和 self.rank：与 torch.distributed 相关，用于管理当前节点在流水线中的PP Rank（哪个阶段）。

• self.is_first_rank, self.is_last_rank, self.is_in_second_half：标记当前节点（机床）在“流水线”中的位置，是在“左端”还是在“右端”、是前半段还是后半段。

3.2 状态管理与重置

_reset_states 方法

def _reset_states(self) -> None:
    WeightGradStore.clear()

    self.input_chunks = ([], [])
    self.output_chunks = ([], [])
    self.input_grad_chunks = ([], [])
    self.output_grad_chunks = ([], [])
    self.labels = None
    self.loss_chunks = []
    self.criterion = None

    ...
    # 各种计数器，用于追踪当前处理到第几个 chunk
    self.current_f_chunk_id = [0, 0]
    self.current_b_chunk_id = [0, 0]
    ...
    self.comm_ops = []
    self.to_free = []

• _reset_states 就像每次老王接到新订单之前都会清空生产线、重新摆放刀具和记录簿一样：

• WeightGradStore.clear()：将之前存储的需要延迟执行的“参数梯度计算”回调函数全清空，为后续的 Zero-Bubble 或部分重叠做准备。
• input_chunks, output_chunks, input_grad_chunks, output_grad_chunks：相当于流水线里的“在制品”和它们的“梯度信息”。初始化为空的列表是为了逐步把每一批（micro-batch）塞进来再往后传。
• 一系列计数器：用来跟踪当前处理到第几个前向批次、第几个后向批次，或者是已经发送/接收了多少次数据等。

3.3 前向与后向计算：如何在同一设备上实现交叠

3.3.1 _forward_compute_chunk(self, phase)

def _forward_compute_chunk(self, phase: int) -> None:
    phase ^= self.is_in_second_half  # 动态修正 phase
    chunk_id = self.current_f_chunk_id[phase]
    self.current_f_chunk_id[phase] += 1
    inputs = self.input_chunks[phase][chunk_id]
    ...
    outputs = self.module[phase](*inputs)
    ...

• 这里先根据 phase 计算出当前实际使用的是哪个模块（如前段模块 or 后段模块）。然后从 input_chunks[phase] 中取出对应批次的数据做前向计算。

• outputs 最终被存进 self.output_chunks[phase]` 中。
• 如果这是最后一个阶段（is_last_stage）并且设置了 criterion，就把损失（Loss）放进 self.loss_chunks 中。想象一下，当车间里把一批零件送到“最后工序”——如果这是老王最信任的质检环节，就同时得出“损失分数”以便后续调整。

3.3.2 _backward_compute_chunk(self, phase, enable_zb: bool = False)

def _backward_compute_chunk(self, phase: int, enable_zb: bool = False) -> None:
    if self.forward_only:
        return
    phase ^= self.is_in_second_half
    chunk_id = self.current_b_chunk_id[phase]
    ...
    if is_last_stage:
        # 在最后一段，直接对 loss 进行 backward
        loss = self.loss_chunks[chunk_id]
        loss.backward()
        loss.detach_()
    else:
        # 对输出和输出梯度执行 run_backward
        outputs = self.output_chunks[phase][chunk_id]
        ...
        run_backward(outputs, output_grads)
    ...
    if enable_zb:
        WeightGradStore.flush()

    # 更新 input_grads
    ...

• 对于“后向阶段”，最重要的是：如果在最末尾的阶段，就直接对 loss 调用 backward()；否则对中间层的 outputs 调用 run_backward，并把梯度传回上一层。

• enable_zb 用于启动 Zero-Bubble（如 ZB1P）策略，即将一些参数梯度的计算缓存在 WeightGradStore 里，并在合适的时机 flush()。这部分正好与我们前面讲的分离“输入梯度计算”和“权重梯度计算”相呼应。
• 当后向回传完毕，拿到上一层（或上一工序）的梯度，就把它存到 self.input_grad_chunks[phase] 里——类似于老王在质量检验后，把修改意见“传回”上一个机床

3.3.3 _forward_backward_compute_chunk(self, phase0, phase1)

def _forward_backward_compute_chunk(self, phase0: int, phase1: int) -> None:
    if self.forward_only:
        self._forward_compute_chunk(phase0)
        return

    if not self.overlaped_forward_backward:
        self._forward_compute_chunk(phase0)
        self._backward_compute_chunk(phase1)
        return

    # 1) pre-forward
    # 2) pre-backward
    # 3) overlaped_forward_backward(...)
    # 4) post-forward
    # 5) post-backward

这是 DualPipe 里最核心的部分：如果 overlapped_forward_backward 为 True，就代表同一个 GPU 支持把前向和后向融合在一起的一种特殊方法（类似“左右手一起做事”）。

• 函数里先从 input_chunks 拿到本批次前向需要的数据，再从 output_chunks 中拿到后向需要的数据，然后调用 module0.overlaped_forward_backward(…)`。
• 这一步好比在车间里，工人先准备好要加工的新零件，同时也把上一批零件的质检报告和所需的调整一并拿来，然后运用同一个机床的“联合加工功能”去完成“前向+后向”的混合操作。
• 最后把新的输出以及梯度分别存回 output_chunks 和 input_grad_chunks。这样就能在同一阶段内，完成对前向与后向的部分操作，而无需像 ZB1P 那样分两次调用或等待另外的阶段。

3.4 通信管理：让“运输时间”隐藏在计算中

在整个大模型流水线并行中，每个阶段的 GPU 都需要频繁地与前一个/后一个 GPU 通信（如在车间里把半成品从铸造机床运给锻造机床）。DualPipe 通过以下几个函数对通信做了拆分和调度，让计算过程与通信过程能够大幅重叠：

• _recv_forward(self, phase) / _send_forward(self, phase) 用于接收/发送“前向输出”或“前向输入”。在车间比喻中，这相当于把加工好的半成品移交到下一台机床。
• _recv_backward(self, phase) / _send_backward(self, phase) 用于接收/发送“后向梯度”或“后向输入”。就像检验报告在车间间的回传。
• _commit_and_wait_comm(self) 先通过 dist.batch_isend_irecv(self.comm_ops) 一次性把所有的非阻塞通信发出去，然后 wait()。这意味着通信和计算可以在不同时间片并行，只有当我们真的需要数据时才会等待。这就把运输时间“隐藏”在机床空闲或机床可以“分配给传输”的那部分时间里了。

3.5 WeightGradStore：延迟梯度更新设计

在后向传播时，我们可能会多次对同样的权重做梯度累加。WeightGradStore 通过一个静态队列缓存了这些更新操作，只有在需要时 pop() 统一执行，有两大好处：

• 减少频繁同步或写内存：不必每个微批都做一次参数更新，可以攒到一个合适的时间点统一处理。
• 搭配流水线：避免打断流水线的并发计算，也方便在某些阶段利用通信空闲时再同步。

class WeightGradStore:
    enabled: bool = False
    cache: List[Callable] = []
    funcs_queue = queue.Queue()

    @classmethod
    def put(cls, func: Callable) -> None:
        cls.cache.append(func)

    @classmethod
    def flush(cls) -> None:
        cls.funcs_queue.put(cls.cache)
        cls.cache = []

    @classmethod
    def pop(cls) -> None:
        funcs = cls.funcs_queue.get()
        for func in funcs:
            func()

3.6 整体调度：step(…) 方法中的 8 大步骤

最核心的应用逻辑在 step(…) 里。这函数就像老王给所有机床派发指令的“总调度”——为了实现 DualPipe 的双向流水线，需要做以下阶段性动作（简化理解，可结合源码的注释）：

1. Step 1：nF0 在流水线开始时，让一端的机床率先处理一定数量的前向批次。这就像在传送带还没正式转动前，前面几道工序先把一部分原材料“初加工”起来，后面工序暂时闲置。
2. Step 2：nF0F1 逐步让另一端也开始前向操作，使两个方向都被激活，通过 _forward_chunk(0) 和 _forward_chunk(1) 的交替来实现双向注入。
3. Step 3：nB1W1F1 在某些批次开始出现后向时，先将后向（_backward_chunk(1)）和前向（_forward_chunk(1)）混合进行，并调用 _weight_chunk() 来执行延迟的权重更新操作（ZeroBubble 相关）。
4. Step 4：nF0B1F1B0（主循环） DualPipe 通过 _forward_backward_chunk(0,1) / _forward_backward_chunk(1,0) 实现对前向和后向的同步调度，也就是最主要的“互相交织”步骤。
5. Step 5：nB1F1B0 后向与前向继续往返推进，做进一步交错。
6. Step 6：nB1B0 更集中地执行后向，让之前拆分在 WeightGradStore 的梯度处理也得以不断刷新。
7. Step 7：nWB0 继续执行“权重更新 + 后向计算”。

8. Step 8：nW 收尾阶段的权重更新，确保所有操作都顺利结束。

3.7 代码总结

这样做带来的好处是显而易见的：

1. 流水线气泡最小：DualPipe 真正实现了“前后向同时上阵”，降低了串行等待。
2. 通信被大幅重叠：借助 _commit_and_wait_comm() 的异步发送/接收，很多跨节点的 all-to-all 或 pipeline 通信在 GPU 计算“间隙”里就完成了。
3. 可扩展性：即便分布式训练规模变大（更多 GPU、更多节点），只要保持一定计算-通信比例，就能继续让这种“重叠”有效发挥。

4. 显存优化：把最浅层与最深层放在同一个 PP Rank 并做必要的 Zero-Bubble，减少中间存储浪费。

总结与展望

（文：PaperWeekly）