
AIxiv专栏是机器之心发布学术、技术内容的栏目。过去数年,机器之心AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com

-
论文标题:CL-DiffPhyCon: Closed-loop Diffusion Control of Complex Physical Systems
-
论文链接:https://openreview.net/pdf?id=PiHGrTTnvb
-
代码地址:https://github.com/AI4Science-WestlakeU/CL_DiffPhyCon
-
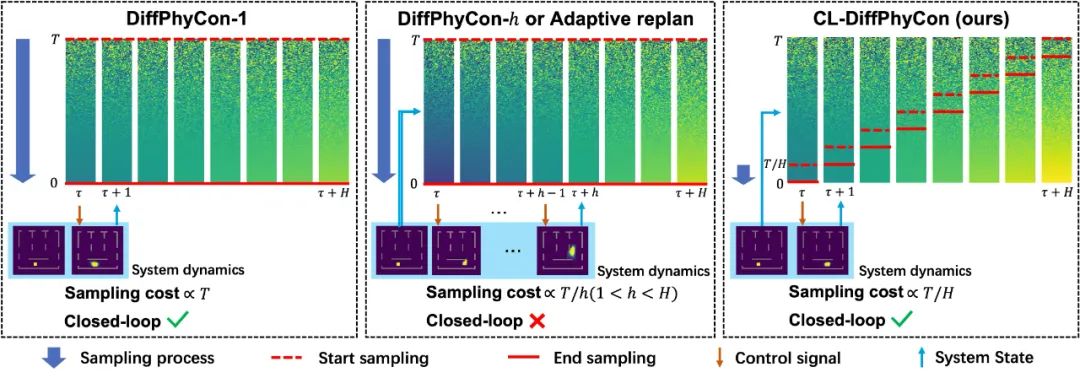
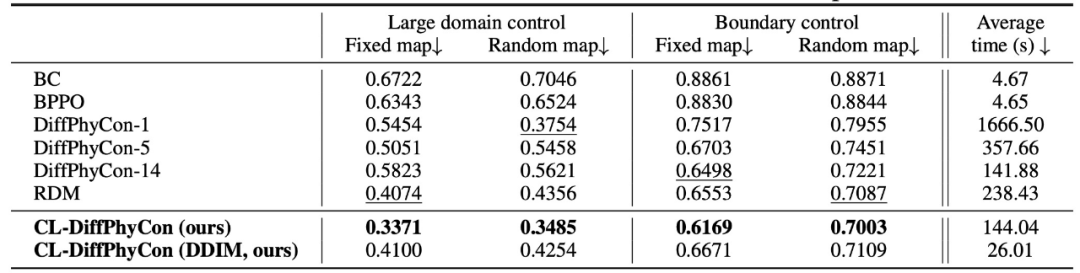
高效采样:CL-DiffPhyCon 通过异步去噪框架,能够显著减少采样过程中的计算成本,提高采样效率。与已有的扩散控制方法相比,CL-DiffPhyCon 能够在更短的时间内生成高质量的控制信号。
-
闭环控制:CL-DiffPhyCon 实现了闭环控制,能够根据环境的实时反馈不断调整控制策略。相比已有的开环扩散控制方法,提高了控制效果。
-
加速采样:此外,CL-DiffPhyCon 还能与 DDIM [5] 等扩散模型的加速采样技术结合,在维持控制效果基本不变的前提下,进一步提升控制效率。
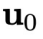 、系统动力学G以及特定的控制目标
、系统动力学G以及特定的控制目标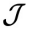 ,本文考虑如下复杂系统的控制问题:
,本文考虑如下复杂系统的控制问题: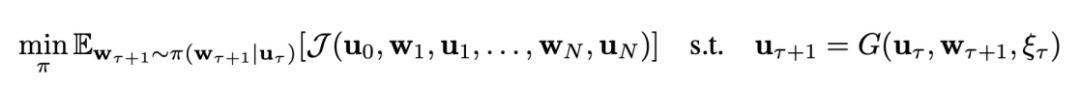
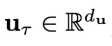 和
和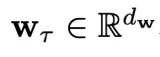 分别是物理时间步
分别是物理时间步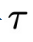 时的系统状态和外部控制信号,轨迹的长度为N。系统动力学G代表系统在外部控制信号下随时间的状态转移规则。G可以是随机性的,存在非零随机噪声
时的系统状态和外部控制信号,轨迹的长度为N。系统动力学G代表系统在外部控制信号下随时间的状态转移规则。G可以是随机性的,存在非零随机噪声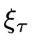 ;也可以是确定性的,即
;也可以是确定性的,即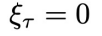 。为了让问题设置更具一般性,状态的演变只能通过实际测量来观测,即假设G的表达形式不一定可以获得。本文中关注闭环控制,意味着每个时间步的控制信号
。为了让问题设置更具一般性,状态的演变只能通过实际测量来观测,即假设G的表达形式不一定可以获得。本文中关注闭环控制,意味着每个时间步的控制信号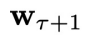 是从以当前状态
是从以当前状态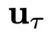 为条件的一个概率分布中采样得到的。这区别于开环控制或者规划(planning)方法,即每次规划未来多个时间步的控制信号后,将其依次应用到环境中,并且在此期间不利用环境反馈进行重新规划。
为条件的一个概率分布中采样得到的。这区别于开环控制或者规划(planning)方法,即每次规划未来多个时间步的控制信号后,将其依次应用到环境中,并且在此期间不利用环境反馈进行重新规划。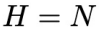 内所有的控制信号,并依次将其用于系统的控制过程。为了记号方便,引入变量
内所有的控制信号,并依次将其用于系统的控制过程。为了记号方便,引入变量 表示第
表示第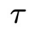 物理时间步系统状态和控制信号的拼接。该方法包含以下过程:
物理时间步系统状态和控制信号的拼接。该方法包含以下过程:-
首先离线收集大量的轨迹数据,每条轨迹包括初始状态、控制序列和相应的状态序列。
-
然后,用这些离线轨迹训练一个去噪步数为T,物理时间窗口为N的扩散模型,并将所有物理时刻的系统状态和控制信号的联合隐变量
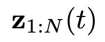 作为扩散变量。这里在记号
作为扩散变量。这里在记号 中,用下角标表示物理时间
中,用下角标表示物理时间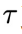 或其所处的区间,用括号里的t表示扩散步骤。在扩散过程中,随着t增大,
或其所处的区间,用括号里的t表示扩散步骤。在扩散过程中,随着t增大,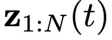 中的噪声程度逐渐增加:
中的噪声程度逐渐增加: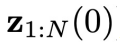 不含噪声,
不含噪声, 为高斯噪声。
为高斯噪声。 -
在去噪过程(实际控制过程)中,以系统的初始状态
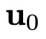 为条件,利用训练的扩散模型,在控制目标
为条件,利用训练的扩散模型,在控制目标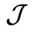 的梯度引导下,让t从T 降到 0,将高斯噪声
的梯度引导下,让t从T 降到 0,将高斯噪声 逐步去噪为不含噪声的
逐步去噪为不含噪声的 ,其中包含控制序列
,其中包含控制序列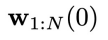 和对应产生的状态序列
和对应产生的状态序列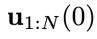 。
。 -
最后,将控制序列
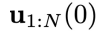 逐步输入到环境中,实现对系统的控制。
逐步输入到环境中,实现对系统的控制。
-
同步联合隐变量:
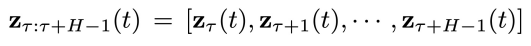 表示在物理时间区间
表示在物理时间区间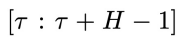 内,对每个分量加入相同程度噪声。这里t的取值范围是 0 到T。
内,对每个分量加入相同程度噪声。这里t的取值范围是 0 到T。 -
异步联合隐变量:
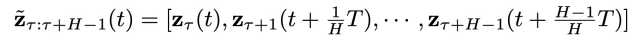 表示在物理时间区间
表示在物理时间区间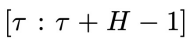 内,为越晚的物理时间赋予越高的噪声程度,即实现了物理时间和去噪进度的解耦。这里t的取值范围是 0 到
内,为越晚的物理时间赋予越高的噪声程度,即实现了物理时间和去噪进度的解耦。这里t的取值范围是 0 到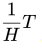 。
。
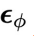 和异步扩散模型
和异步扩散模型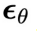 。
。 :
: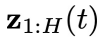 当中每个分量包含的噪声。它只用于
当中每个分量包含的噪声。它只用于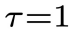 的物理时刻。训练损失如下:
的物理时刻。训练损失如下: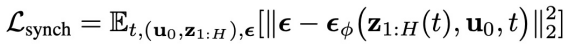
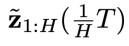 ,这是物理时间上最早的异步联合隐变量。采样方法如下:对于给定的初始条件
,这是物理时间上最早的异步联合隐变量。采样方法如下:对于给定的初始条件 ,类似于 DiffPhyCon 的去噪过程,从高斯噪声
,类似于 DiffPhyCon 的去噪过程,从高斯噪声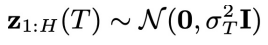 开始,让t从T逐步减少到
开始,让t从T逐步减少到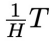 ,在每步迭代中,从
,在每步迭代中,从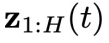 当中减去
当中减去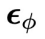 预测的噪声,同时减去控制目标
预测的噪声,同时减去控制目标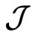 的梯度。这样就采样得到了一系列同步联合隐变量
的梯度。这样就采样得到了一系列同步联合隐变量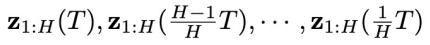 。再从其中取 “对角线”,就能得到初始的异步联合隐变量
。再从其中取 “对角线”,就能得到初始的异步联合隐变量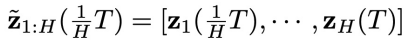 (图 2 的 (2) 子图中的虚线红框)。
(图 2 的 (2) 子图中的虚线红框)。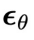 :
: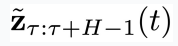 中每个分量包含的噪声。它用于
中每个分量包含的噪声。它用于 的所有物理时刻。它的训练损失如下:
的所有物理时刻。它的训练损失如下: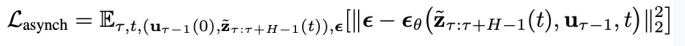
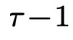 个物理时刻的系统状态
个物理时刻的系统状态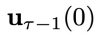 和异步联合隐变量
和异步联合隐变量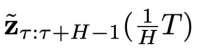 的条件下,采样
的条件下,采样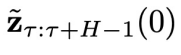 ,即实现解耦的异步去噪。采样方法如下:从
,即实现解耦的异步去噪。采样方法如下:从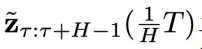 开始,让t从
开始,让t从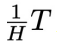 逐步减少到 0,在每一步中,从
逐步减少到 0,在每一步中,从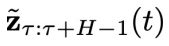 当中逐分量减去
当中逐分量减去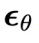 预测的噪声,同时减去控制目标
预测的噪声,同时减去控制目标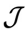 的梯度,最终得到
的梯度,最终得到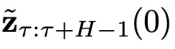 。
。-
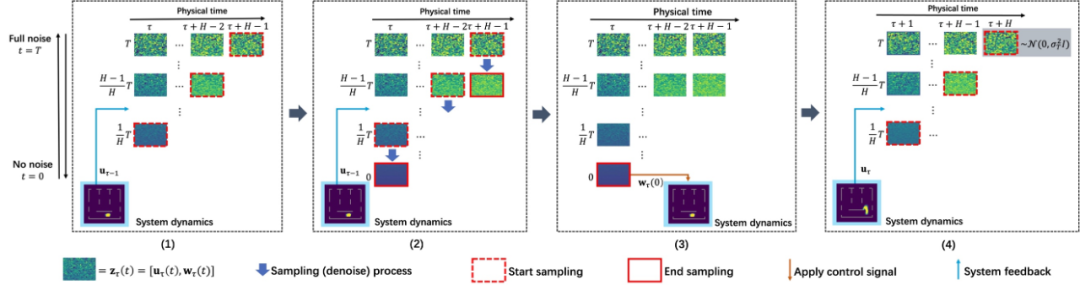
第(1)步:在第 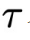 个物理时间步,获得物理时间窗口
个物理时间步,获得物理时间窗口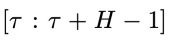 内的初始状态
内的初始状态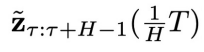 和系统状态
和系统状态 。特别地,当
。特别地,当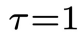 时,通过上文的同步扩散模型
时,通过上文的同步扩散模型 采样得到
采样得到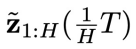 。
。 -
第(2)步:以 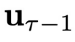 为采样条件,利用异步扩散模型
为采样条件,利用异步扩散模型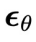 ,从
,从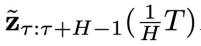 开始连续采样
开始连续采样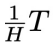 步,得到
步,得到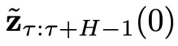 。
。 -
第(3)步:将  的第 1 个分量
的第 1 个分量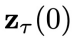 中包含的控制信号
中包含的控制信号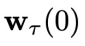 输入到环境中,得到下一个状态
输入到环境中,得到下一个状态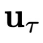 。
。 -
第(4)步:采样一个高斯噪声  ,拼接到第(2)步采样得到的
,拼接到第(2)步采样得到的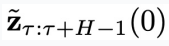 的最后
的最后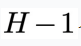 个分量的结尾,得到物理时间窗口
个分量的结尾,得到物理时间窗口 内的初始状态
内的初始状态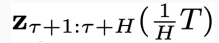 ,同时将
,同时将 作为条件,进入下一个物理时间步
作为条件,进入下一个物理时间步 。
。
 进行建模,并在控制目标的引导下采样。本文将如下的增广 (augmented) 联合分布作为分析的出发点:
进行建模,并在控制目标的引导下采样。本文将如下的增广 (augmented) 联合分布作为分析的出发点: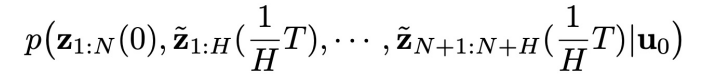
 (包含于
(包含于 )。而之所以要研究这个增广联合分布,是因为它指引着我们让
)。而之所以要研究这个增广联合分布,是因为它指引着我们让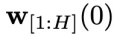 变得 “可被采样”。论文研究发现,这个看似复杂的增广联合分布其实具有一个有趣的规律:假设联合分布
变得 “可被采样”。论文研究发现,这个看似复杂的增广联合分布其实具有一个有趣的规律:假设联合分布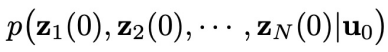 满足 Markov 性质(这是强化学习等决策类问题中常见的假设),那么从增广联合分布中采样的问题,就可以转化为只从两类分布中采样的问题:即先从一个初始分布
满足 Markov 性质(这是强化学习等决策类问题中常见的假设),那么从增广联合分布中采样的问题,就可以转化为只从两类分布中采样的问题:即先从一个初始分布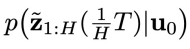 中采样得到
中采样得到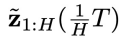 ,再从一个转移分布
,再从一个转移分布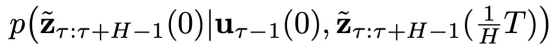 中依次采样,得到一系列
中依次采样,得到一系列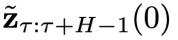 (
(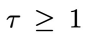 )。具体地,该采样过程可以用如下定理描述:
)。具体地,该采样过程可以用如下定理描述:
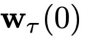 时,所依赖的系统状态
时,所依赖的系统状态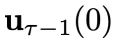 可以从环境反馈中得到。这是因为我们已经采样得到了上一个时刻的控制变量
可以从环境反馈中得到。这是因为我们已经采样得到了上一个时刻的控制变量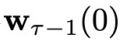 ,因此可以立即将其输入到环境中,得到环境反馈的
,因此可以立即将其输入到环境中,得到环境反馈的 。也就是说,这个采样过程能够满足闭环控制的要求。
。也就是说,这个采样过程能够满足闭环控制的要求。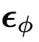 的作用是从
的作用是从 中采样,而异步扩散模型
中采样,而异步扩散模型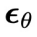 的作用是从
的作用是从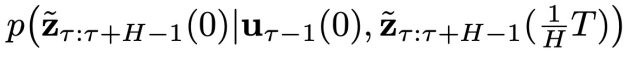 中采样。所以,我们只需要这两个扩散模型就能够实现从轨迹数据分布中采样,再通过在采样过程中加入控制目标的梯度引导,就可以优化控制目标。
中采样。所以,我们只需要这两个扩散模型就能够实现从轨迹数据分布中采样,再通过在采样过程中加入控制目标的梯度引导,就可以优化控制目标。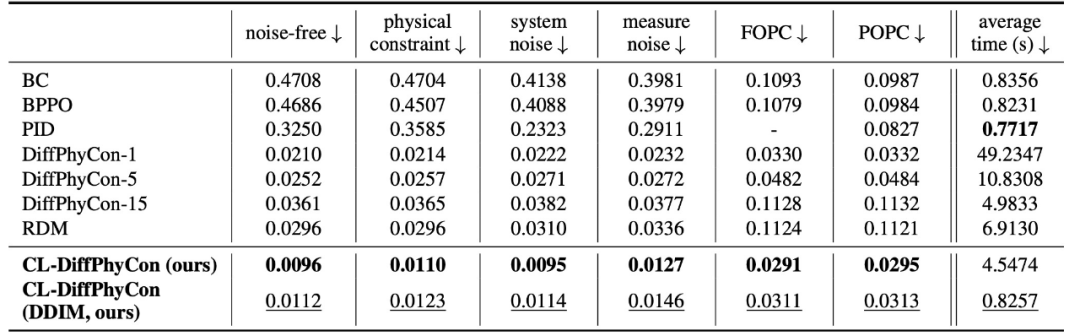

(文:机器之心)

