一水 发自 凹非寺
量子位 | 公众号 QbitAI
韦东奕论文再登数学顶刊!
就在备受关注之际,韦神本韦和另两位北大学者章志飞、邵锋合作的一篇论文已发表于数学界顶级期刊《Forum of Mathematics, Pi(数学论坛,π) 》。
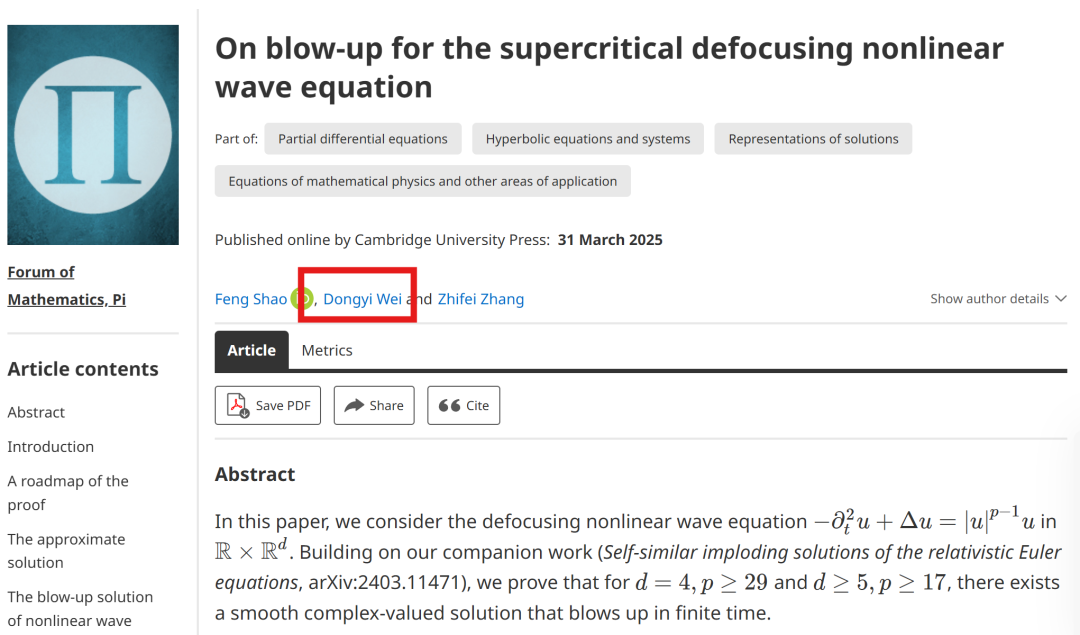
论文题目为《On blow-up for the supercritical defocusing nonlinear wave equation(超临界散焦非线性波动方程的爆破现象研究)》,通俗来说就是研究某些方程的解在什么条件下会“爆炸”失控。
而经过一系列论证,他们最终发现对于d=4且p≥29,以及d≥5且p≥17的情况,存在一个在有限时间内爆破的光滑复值解。
不清楚具体研究内容不要紧,重要的是这一成果不仅填补了相关空白,而且其证明方法绕过了传统方法中奇点处理的难点,理论上可推广到其他非线性偏微分方程的爆破研究。
网友们的反应一致be like:
字都认识,但是看不懂一点(doge)。
实际上,据清华大学丘成桐数学科学中心网站介绍,韦东奕还在今年5月以主讲人的身份做了这篇论文的报告。
下面具体来看这项研究讲了啥?
将散焦方程的爆破性研究扩展至d≥4
从论文摘要入手,该研究探讨了在ℝ×ℝd上,以下散焦非线性波动方程:
1)在“超临界”状态下是否会在有限时间内爆破?
2)如果存在,爆破的速度和机制是什么?
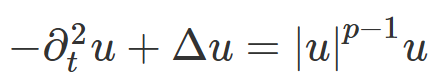
正如水波、电磁波等波动现象能用方程来描述,“非线性波动方程”是指一类描述复杂波动的数学方程。
而这里的“散焦”意味着波的能量向外扩散。
那么,为什么要关注该方程在“超临界”状态下的情况呢?
原因主要在于,此前研究已解决“亚临界”、“临界”情况的全局正则性(解永远存在且光滑),但超临界散焦方程的爆破性研究很少,尤其在空间维度d≥4的低维情形几乎空白。
而通常来说,当方程处于“超临界”状态时,波的能量分布更难控制,更可能出现“爆破”现象(即解在有限时间内变得无穷大)。
所以,韦东奕等人想要论证:
在d≥4的低维情形下,散焦非线性波动方程存在有限时间爆破解。
这里要补充一下,方程的“临界性”由空间维度d和指数p决定。几种状态的定义如下:
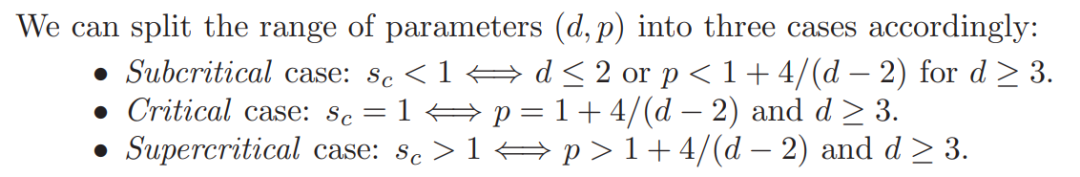
其中“超临界”状态具体指sc >1,即当且仅当d≥3,有p>1+4/(d-2)。
最终,他们得出了两项核心结论:
-
当d=4且p≥29,以及d≥5且p≥17的情况时,存在光滑的初始波形,使得方程的解在有限时间内爆破。
-
波的最大振幅随时间接近爆破时间时,爆破速度比临界范数的增长更快,说明爆破不可避免。

具体论证方法则结合了三人组之前关于“相对论欧拉方程自相似内爆解”的一项研究。
这篇名为《Self-similar imploding solutions of the relativistic Euler equations》的论文核心围绕相对论欧拉方程展开,这是一个描述理想流体(比如气体)在相对论速度下行为的数学模型。
团队研究了这些方程的一种特殊解,叫做“自相似内爆解”,即流体在有限时间内会集中到一个点,就像内爆一样。
他们发现,在特定的条件下(比如在2维或3维空间中,或在更高维度中但条件稍微宽松一些),这种内爆解是存在的。
这个发现对于理解更复杂的波动方程(比如描述声波或光波的方程)在特定条件下是否会在有限时间内“爆炸”(即变得无限大)非常重要。
换言之,我们能更好地理解在极端条件下,物质和能量的行为方式。

回到正题,在后来登上顶刊的这项研究中,他们正是将相对论欧拉方程的“自相似解”(形状不变、仅缩放的解)作为爆破解的“骨架”,结合其他技术绕过了传统方法中奇点处理的难点。
最终为理解散焦方程的动力学行为提供了新视角,并且其方法可推广到其他非线性偏微分方程的爆破研究。
通俗理解,其具体论证过程可分为以下五个步骤:
第一步:模相位分解。就像把光分解成振幅和相位一样,他们将波也拆成“幅度”和“相位”两个零件,以便单独研究哪个零件导致了“爆破”。
第二步:自相似解假设。一般炸弹爆炸时,不同时间点的“爆炸形态”其实很像,只是“缩放了大小”,故他们也假设波的爆破也有这种“自相似”,以便后续计算。
第三步:构造近似解。继续用简单的数学公式拼出一个“假波”,模仿爆破的趋势。
第四步:反向时间求解精确解。从“爆炸结局”往回推,慢慢修正成精确解,以证明真的存在这样一个波,会在特定时刻爆炸。
第五步:推论的证明。通过前面四步,已经找到“会爆炸的波”的精确解,现在要验证它的 “爆炸速度”。而通过计算,他们发现爆炸“刹不住车”,必然会发生。
更专业的论证过程指路原论文第二章节。

曾以唯一作者身份登上数学顶刊
这项研究的其他两位作者分别为章志飞和邵峰。

章志飞,博士毕业于浙江大学,目前为北大数学科学学院博雅特聘教授、副院长和博士生导师。
主要从事偏微分方程领域的研究,已在Invent Math、CPAM、Memoirs AMS等顶尖数学刊物上发表论文150余篇,获得过国家“杰青”和陈省身数学奖等荣誉。
他和韦东奕合作多年,2022年曾作为团队代表在国际数学家大会上做了45分钟的报告。

邵峰,本科毕业于中国科学技术大学,目前是北大基础数学专业四年级博士生。
章志飞和韦东奕为邵峰的共同导师,三人多次合发论文。

事实上除了合著,韦东奕的个人研究也曾登上数学顶刊。
就在2021年,《Science China – Mathematics》刊载了他的一篇论文“通过预解估计流体流动中的扩散和混合”。
怕大家信息过载,具体内容这里不再展开了(doge)~

BTW,许多网友关注到韦东奕在这篇论文中并非第一署名。
根据网友科普,这是因为数学上默认按照姓氏字母顺序排序,不区分一二作。

论文:
https://arxiv.org/abs/2405.19674
— 完 —
📪 量子位AI主题策划正在征集中!欢迎参与专题365行AI落地方案,一千零一个AI应用,或与我们分享你在寻找的AI产品,或发现的AI新动向。
💬 也欢迎你加入量子位每日AI交流群,一起来畅聊AI吧~

一键关注 👇 点亮星标
一键三连「点赞」「转发」「小心心」
欢迎在评论区留下你的想法!
(文:量子位)

