
©PaperWeekly 原创 · 作者 | 苏剑林
单位 | 科学空间
研究方向 | NLP、神经网络
在文章《Transformer升级之路:MLA好在哪里?(上)》中,我们对 MLA 相比常见 MHA、GQA、MQA 的一些变化分别做了消融实验,其中的变化包括“增大 head_dims”、“Partial RoPE” 和 “KV 共享”,实验的初步结果是这三个变化很可能都是 MLA 效果优异的原因。
本文我们将从一个更加偏理论的角度出发,来理解 MLA 的成功之处。

部分旋转
首先,我们把最终的断言放在前面:
在相同训练成本和推理成本下,MLA 可能是效果最好的 Full Attention 变体。
很明显,这个判断把 MLA 摆在了非常高的位置。这是在比较理想和简化的假设下,根据上一篇文章的实验结果以及本文接下来的理论分析所得的结论。由于实际的训练和推理存在诸多复杂的因素,所以该结论大概率会有所偏差,但我们至少可以得出,MLA 应该是走在了正确的改进方向上。
MLA 之所以能够表现出色,有一个非常大的前提,那就是部分旋转的 Partial RoPE 效果不逊色于甚至可能优于完全体的 RoPE。
这里的 Partial RoPE 可以有两种含义:一是我们对 Attention 的 、 加 RoPE 时,可以只对小部份维度加,剩下的维度保持不变;二是我们可以考虑层间 RoPE 与 NoPE 交替出现,并且 NoPE 的层可以占多数。
说白了,RoPE 可以只加“一点点”,但不能不加,完全不加的话效果不行。如果需要理论,笔者比较认同《Transformer升级之路:RoPE的底数选择原则》的解释,大致意思是 Partial RoPE 使得检索结果更兼顾位置与语义。
此外,像 FoX [1]、SBA [2] 等新工作也体现出一定潜力,但对于 MLA 来说,这些变体就相当于 NoPE,因此不改变结论。
“Partial RoPE 效果不差”的结论,允许我们把 Attention 的主要计算复杂度放到 NoPE 部分上,这提供了更大的腾挪空间,MLA 便是得益于此。

键值共享
Full Attention 的变化大致上是从 MHA、MQA [3]、GQA [4] 然后到 MLA,虽然 MQA 可以看作是 GQA 的特例,但按时间顺序来说确实是 GQA 在后。
在 MLA 之后,还出现了 MFA [5]、TPA [6] 两个变体。这些变体本质上都是在尽量保持效果的前提下,尽可能压榨 KV Cache 以提高生成速度。
简单来说,Attention 模型的复杂度可以分训练、Prefill 和 Decoding 三部分,其中训练和 Prefill 是相似的,所以本质上是 Prefill 和 Decoding 两部分。
Prefill 是指模型处理输入、直至吐出第一个 token 的阶段,这部分我们下节再谈;Decoding 是指 Token by Token 的生成阶段,它可以通过 KV Cache 机制来加速,但同时也导致了 KV Cache 大小几乎是 Decoding 速度的唯一瓶颈。
所以,压缩 KV Cache 就是提高 Decoding 速度。现在问大家一个问题:在 NoPE 背景下,给定 KV Cache 大小后,效果最好的 Attention 是什么呢?如果不考虑参数量差异,只在单层 MHA/GQA/MQA 内讨论(TPA 和 MFA 我们后面再补充讨论),那么答案将会是:
一个 head_dims 等于 KV Cache 大小、K 和 V 共享的 MQA。
看上去是不是让人意外?其实不难理解。因为 MHA、MQA 都可以看成是 GQA 的一个特例,所以我们只需要分析 GQA,我们在《缓存与效果的极限拉扯:从MHA、MQA、GQA到MLA》已经给出了,GQA 可以重新表示成一个K、V拼接起来的模型:
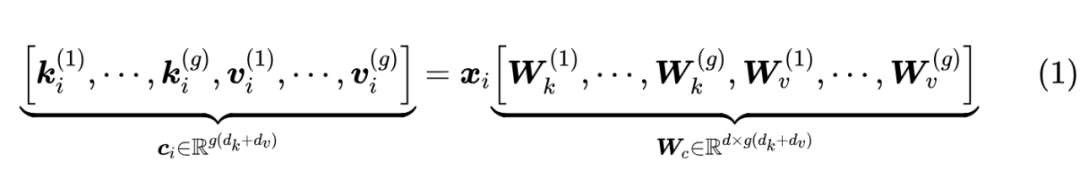
这里 正是单个 Token 的 KV Cache 总大小。接着我们算 Attention 的时候, 到 的变换分别吸收到 和 那边去,那么就得到了一个 K、V 都是 的 MQA。
所以说,“head_dims 等于 KV Cache 大小、K 和 V 共享的MQA”,实际上是给定 KV Cache 大小后 MHA/GQA/MQA 的“超集”,那么它自然是理论上效果最好的选择。

双重投影
综上所述,如果我们想要在相同 Decoding 速度下效果最优,那么应该训练一个指定 head_dims 的、KV 共享的 MQA,比如约定 KV Cache 不超过 512,那么 head_dims=512 的、KV 共享的 MQA 就是最佳选择。
事实上,MLA 在 Decoding 阶段正是 KV 共享的 MQA(NoPE 部分),这就是它走在正确方向上的体现之一。
然而,将 head_dims 升到 512,Decoding 是没问题,但训练和 Prefill 都很难接受,因为它们俩的瓶颈是计算,而影响计算速度的主要因素是 num_heads 和 head_dims。
为了保证效果,num_heads 变动的空间不大,因此 head_dims 大小可以说是计算量的唯一指标,head_dims 升到 512 意味着计算量要增加到原来的4倍(相比 head_dims=128)。
现在再来问大家一个问题:同样在 NoPE 背景下,给定 num_heads 和 head_dims 后,效果最好的 Attention 是什么呢?
这个问题的答案我相信大家都能接受,那就是 MHA,因为它限制最少。所以,单从训练和 Prefill 成本来看,我们希望的是训练一个 head_dims=128 的 MHA。
怎么调和 Prefill 与 Decoding 这两个不同的期望呢?这就是 MLA 的“大招”了,它通过两步投影得到 K、V:先将输入投影到单个 512 维的向量,然后将该向量投影到多个 128 维的向量,然后利用 “Attention + NoPE” 固有的恒等变换性质,可以让模型在 MHA-128 和 MQA-512 间自由切换。


总而言之
我们将前面的推理逻辑做个总结:
1. 大前提:Partial RoPE 的效果不差于甚至可能优于 RoPE,这使得我们可以把主要精力放在 NoPE 上;
2. Decoding 主要瓶颈是 KV Cache,理论效果最优的模型是 head_dims=KV Cache、KV 共享的 MQA;
3. 训练和 Prefill 的主要瓶颈都是 head_dims,理论效果最优的模型是 head_dims 为期望值的 MHA;
4. 在 NoPE 前提下,Attention 具有恒等变换性质,可以通过 LoRA 来尽可能地兼顾两个理想方向,这正好是 MLA 所做的。
剩下的,就是给 K 拼接一个共享的低维 RoPE,以最小的成本给 MLA 补充上位置信息,同时还“一箭双雕”:拼接 RoPE 的做法暗合了 “Partial RoPE”,同时也增加了 head_dims,这跟上一篇文章的结论相符。
换句话说,有意或者无意之中使用了 Partial RoPE 和增加了 head_dims,是 MLA 在极致压缩之下还能媲美 MHA 的主要原因。
从 MQA 的角度看,MLA 是给 Q 加了 rank=128 的 LoRA;从 MHA 的角度看,MLA 是给 K、V 加了 rank=512 的 LoRA。
可以说,MLA 是一场 NoPE 结合 LoRA、MHA 结合 MQA 的极致“魔术秀”,成功实现了 Prefill 和 Decoding 的“双向奔赴”。
当然,上述思考过程肯定有一些过于简化的地方。比如,实际的训练和推理还有诸多细节因素,笼统地归结为 head_dims 和 KV Cache 是不完全准确的,例如 MQA 在 Decoding 阶段无法 TP(张量并行),这可能会带来新的效率问题。
还有,分析过程中我们也没有特别注重参数量的对齐,比如在 head_dims=128 时我们也可以考虑增加 Q、K、V 的投影复杂度来提高性能,而不一定要增大 head_dims;等等。
总之,上下两篇文章旨在提供一些实验和思考,来论证 MLA 在一定范围内的最优性。
当然,MLA 是 DeepSeek 首先提出的,第三方使用 MLA 总会给人一种复制 DeepSeek 的感觉,但在更好的变体出现之前,或者在发现严重的缺陷之前,MLA 始终是一个相当有竞争力的选择,如果单纯是为了显示自己不“追随” DeepSeek 而不用 MLA,那是一个相当不明智的选择。
举个例子,现在 Linear Attention 和 Softmax Attention 的混合模型也体现出极大的竞争力,但如果我们将 Linear Attention 跟 LLAMA 使用的 GQA8-128 按 3:1 混合,那么 KV Cache 大致上降低到 GQA8-128 的 1/4,然而 MLA 本身就能将 KV Cache 降低到 GQA8-128 的 1/4 了。

补充讨论
前面我们都在围绕 MHA、GQA、MQA 和 MLA 讨论,这一节我们来简单聊聊两个比较少谈及的 Attention 变体:TPA 和 MFA。
TPA 全称是 Tensor Product Attention,作者给它安了个 Tensor Product 的名字,显得比较“唬人”,实际上它是一个介乎 GQA 和 MLA 的中间产物。
我们以目标 KV Cache=512 为例,TPA 先投影得到一个 512 维向量,然后 reshape 为(4, 128),然后分成两个(2,128)分别代表 K Cache 和 V Cache。到目前为止,TPA 的做法都跟 GQA2-128 一致。
接下来,TPA 借鉴了 MLA 的思想,将(2,128)的 K/V 重新投影成 Multi-Head,但它不是像 MLA 那样整个向量投影,而是沿着 “2” 所在的维度投影,说白了就是将 2 个 128 维向量做 head_dims 次不同的线性组合。
显然,这样 TPA 的上限是不如 MLA 直接从整个 512 维向量出发来投影的。为了缓解这个问题,TPA 又引入了 data-dependent 的组合系数来增强 K、V 的表达能力,即便如此,笔者还是认为它上限不如 MLA。
为什么 TPA 要这样设计呢?大体上是为了兼容 RoPE,这也是它相比 MLA 的最大“优点”。
然而,这里的“优点”是要加个双引号的,因为在 Partial RoPE 不逊色甚至还可能更优的背景下,兼容 RoPE 就有点啼笑皆非的感觉了。
还有,TPA 这样设计,堵死了它升 head_dims 的空间,比如 head_dims 想要升到 256,那么 K Cache、V Cache 就只是(1,256)形状了,单个向量没有线性组合的自由度。
再来看 MFA,它全称是 “Multi-matrix Factorization Attention”,这个名字看上去也有点“唬人”,它实际上就是一个带有 Q-LoRA 的、head_dims=256 的 MQA。
看到这个配置,是不是有点熟悉?因为这配置跟我们上一篇文章的结论完全吻合——增大 head_dims 到 256 来提升 MQA 的效果,并且 KV Cache 跟 MLA 接近,同时通过 Q-LoRA 来控制参数量。
所以,MFA 能“打” MLA,笔者并不意外,上一篇文章我们也实验过差不多的做法了。
此外,上一篇文章我们还提出另外两个提升 MQA 效果的方向,一个是本文已经多次提及的 Partial RoPE,另一个是通过 QKVO-RoPE [7] 的方式实现完全的 KV 共享,让 MQA 变成 GQA2-256,这两点叠加上去,MFA 应该还能再涨一点。

文章小结
本文在上一篇文章的实验结果基础上,给出一个偏理论的思考过程,以论证 MLA 在一定范围内的最优性。总的来说,在 Partial RoPE 的背景下,MLA 似乎是一个非常难以超越的 Attention 变体。
(文:PaperWeekly)


