
随着大语言模型(LLMs)在各类推理应用上效果的持续提升,特别是数学基准测试(benchmark)上频繁刷榜,关于它们“是否真正理解数学”的讨论也日益增多。
针对这一问题,中国科学技术大学认知智能全国重点实验室的研究团队近日提出了一项全新研究成果——CogMath:一个从人类认知视角出发,系统分析大模型数学能力的评估框架。
CogMath 基于人类认知理论,将数学推理过程系统地划分为三个关键阶段:问题理解、问题求解、答案总结。在此基础上,首次提出了涵盖九大核心维度的数学能力评估体系,并据此构建了系统性、可解释的评估基准,旨在实现对大语言模型数学能力的细粒度分析。
该研究成果已被人工智能领域顶级国际会议 ICML 2025 正式接收。

论文地址:
https://arxiv.org/abs/2506.04481
代码地址:
https://github.com/Ljyustc/CogMath

从人类认知出发:九维度数学能力评测体系
数学推理的核心不只是得出正确答案,更在于在解决问题过程中展现出的思维和认知能力。为更系统地理解与评估这一能力,本文构建了一个基于数学推理三阶段认知过程的评测体系。
具体而言,如图 1 所示,本文将数学推理过程划分为 3 个阶段:问题理解(Problem Comprehension)、问题求解(Problem Solving)与答案总结(Solution Summarization)。
以一道应用题为例:“某列火车以每小时 80 公里的速度运行,经过一座长 500 米的桥需要 45 秒,求火车的长度”。
在求解过程中,我们首先在问题理解阶段,需要识别出关键条件(如速度、时间、桥长)并理解它们之间的关系。
接着,进入问题求解阶段,我们需要运用所掌握的数学知识,构建对应的计算表达式,并进行数值计算来得到问题的答案。
最后,在答案总结阶段,我们不仅要验证结果的合理性,还需对整个求解路径进行反思与归纳,形成解决此类问题的方法经验,以便迁移至后续类似任务中。
这一认知链条完整覆盖了人类在解决数学问题中的思维过程,也为评估与提升大语言模型在数学场景中的能力提供了清晰框架与理论支撑。
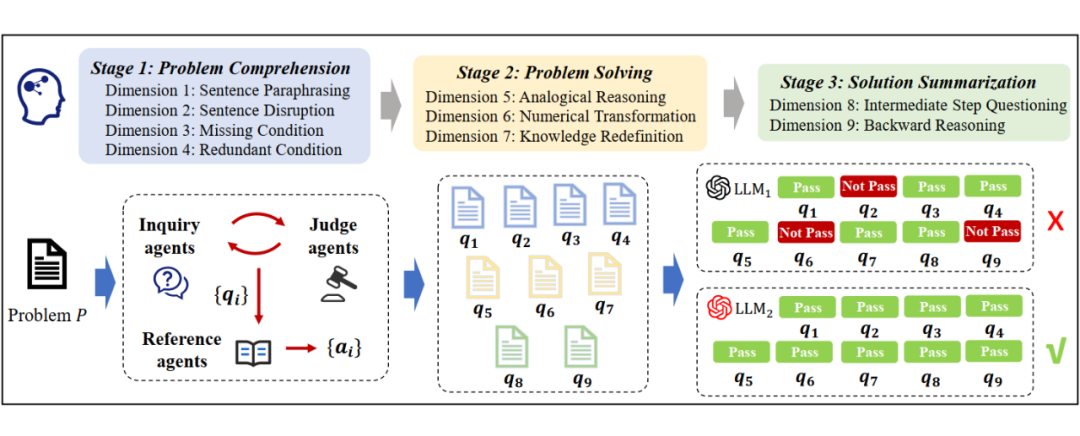
▲ 图1. CogMath 评估框架示意图
在上述三阶段结构基础上,本文进一步细化出 9 个核心评估维度,覆盖语义理解、知识应用、计算能力等多个关键因素。
为了实现对这些能力维度的自动化评估,本文为每个维度配套设计了一个 “Inquiry–Judge–Reference” 多智能体系统。
其中,Inquiry Agent 负责针对该维度,生成问题对应的评估任务(inquiry),Judge Agent 用于对生成的任务进行质量审查与筛选,确保评估内容具有针对性与有效性,Reference Agent 则为每个任务提供高质量的参考答案,用于对大模型或学生的输出进行对比分析与能力刻画。
只有当大模型同时通过 P 对应的 9 个维度的评估任务时,我们才认为模型真正掌握了 P。通过这一机制,系统可在更细粒度上识别模型在不同维度上的优势与短板,为后续能力提升提供有力支撑。
第一阶段:问题理解(Problem Comprehension)
该阶段关注模型对题目文字、语句及数学条件的准确理解,体现出从语义细节到整体结构的认知建构能力。我们从细粒度到粗粒度设计了四个评估维度,逐层揭示模型对数学题目的真实理解水平:
维度1:题目改写(Sentence Paraphrasing)。如果人类真正理解了一个数学问题,即使题目表达方式发生改变(如同义替换或句式调整),仍能准确把握其本质含义。基于此,本维度评估大模型是否具备在表述变动下保持一致的推理准确性。
维度2:题目扰动(Sentence Disruption)。为了规避模型仅凭记忆或关键词匹配作答的情况,本维度采用反事实构造方式。Inquiry Agent 随机打乱原题中各子句的词序,构造出一个人类视角下无法理解的“伪问题”。
此时,如果大模型仍给出与原题相同的答案,则意味着它可能并未真正理解题目,而是记住了这个答案,或者依赖表层的词语模式匹配推理。该维度因此用于识别模型是否在“真正理解”题目基础上做出推理。
维度3:条件缺失(Missing Condition)。理解题目的一个关键在于识别所有必要的已知条件。为此,本维度通过删除题目中的一个关键条件来构造不完整的问题版本。类似维度 2,若模型此时仍给出原始答案,说明它可能基于记忆或表层相似性而非真正理解进行作答。
维度4:条件冗余(Redundant Condition)。与条件缺失相对,本维度在题目中添加一条无关紧要的信息,例如描述性背景或情境性提示。此类条件不应影响最终解答,因此用于评估模型是否能够识别并忽略无关信息,避免其对推理过程造成干扰。

▲ 表1. 问题理解阶段示例
第二阶段:问题求解(Problem Solving)
问题求解阶段需要三种认知要素:解题策略、数值计算以及数学知识。解题策略反映对求解逻辑的把握,数值计算体现算术操作的正确性,而数学知识则是支撑上述两个过程的基础。为此,我们设计了以下三个维度:
维度5:类比推理(Analogical Reasoning)。真正掌握某种解题策略的人类,能够迁移该策略并解决具有相同结构的新问题。为评估模型是否具备这一迁移能力,本维度的 Inquiry Agent 提出一个与原题在解题逻辑和知识要求上一致但题面表述不同的新问题。
维度6:数值变换(Numerical Transformation)。如果模型真正掌握了解题策略,那么仅改变题中的数值不应影响其求解能力。
基于此,本维度通过数值替换生成新的问题(例如表 2 中将 “21” 替换为 “30”)。这种设置能有效检验模型是否将解题过程抽象为可复用的结构。
维度7:知识重定义(Knowledge Redefinition)。人类在面对数学问题时,会利用数学知识(如三角形面积公式)进行推理。但如果一个知识点被重新定义(如“假设三角形面积为三边之和的四倍”),人类能迅速调整思维方式以适应新定义。
为了测试模型是否具备类似的灵活认知能力,Inquiry Agent 在原题基础上引入一个显式的“知识重定义”。Judge Agent 负责确认新定义下的问题仍具可解性,Reference Agent 则基于新定义给出对应答案。

▲ 表2. 问题求解阶段示例
第三阶段:答案总结(Solution Summarization)
在完成问题求解后,人类常常会反思自己的推理过程,总结解决问题所采取的关键步骤与方法论。这种总结不仅有助于加深对特定问题的理解,更促进了对整体解题思维的内化,从而在今后的相似任务中实现迁移。为了评估大模型在该过程的表现,我们设计了以下两个维度:
维度8:中间步骤提问(Intermediate Step Questioning)。人类在学习与理解过程中,往往会将复杂的解题过程拆解为多个可控的中间步骤。评估大模型是否真正理解一个问题,仅凭最终答案是不够的,还需要验证其是否掌握了每一个关键中间推理过程。
因此,在本维度中,Inquiry Agent 提出一个问题,要求模型解释原始解题过程中的某一关键中间步骤。通过该设计,我们可以判断模型是否在每一步均具备逻辑清晰、合理的理解,而非偶然或模式记忆地得出最终答案。
维度9: 反向推理(Backward Reasoning)。反向推理是一项重要且具挑战性的能力。它指的是从完整解答中回推原始信息,模拟人类通过回溯思路来检查是否存在推理漏洞。
该过程可以有效检测模型是否在推理中保持前后逻辑一致性。为测试这一能力,我们的 Inquiry Agent 将原题中的一个关键数值掩码,并要求模型根据原始答案推理出缺失内容。

▲ 表3. 答案总结阶段示例

CogMath 评估结果
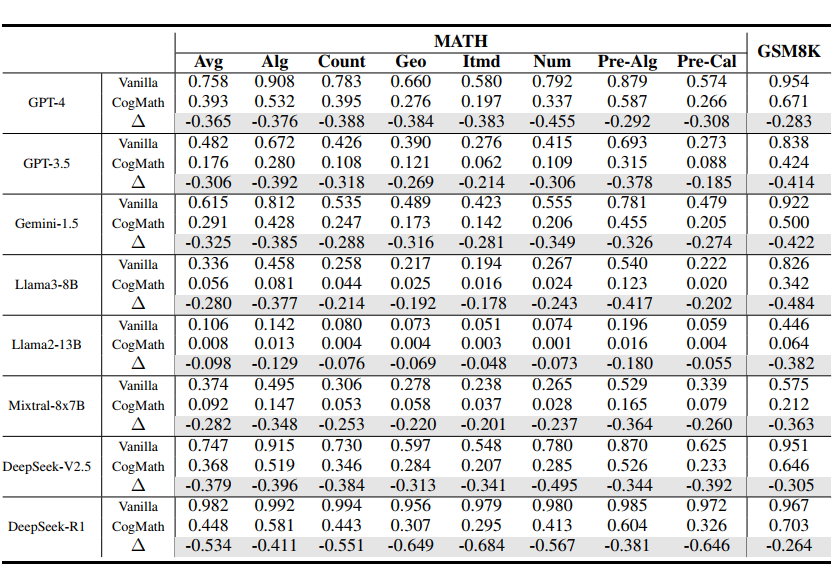
▲ 表4. CogMath 评估结果
结论1:主流评估结果高估大模型数学能力30%-40%
在表 4 中,通过对比在原始数据集(“Vanilla”)与 CogMath 的结果,可以发现所有主流大语言模型的表现均显著下降。
例如,GPT-4 在 MATH 原始数据集上的准确率为 75.8%,而经 CogMath 测试后仅为 39.3%,下降了 36.5%;在 GSM8K 原始数据集上的准确率为 95.4%,但经 CogMath 测试后发现实际只掌握了 67.1%。这表明,现有的基准评估方式高估了模型的真实能力。
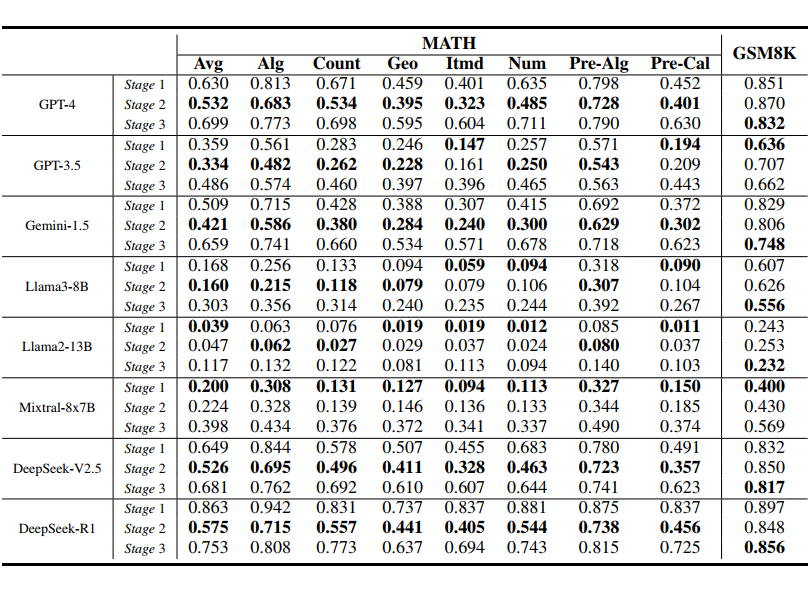
▲ 表5. CogMath 不同认知阶段的评估结果
结论2:不同模型的认知缺陷在不同阶段
CogMath 的一大优势在于能够精准定位不同大模型在推理过程中的薄弱环节。例如,较弱的模型(如 LLaMA2-13B)在“问题理解”阶段就已暴露出明显不足(在表 5 中 Stage 1 表现最差);而较强的模型(如 GPT-4 和 DeepSeek)则在“问题求解”阶段表现出一定的不稳定性。
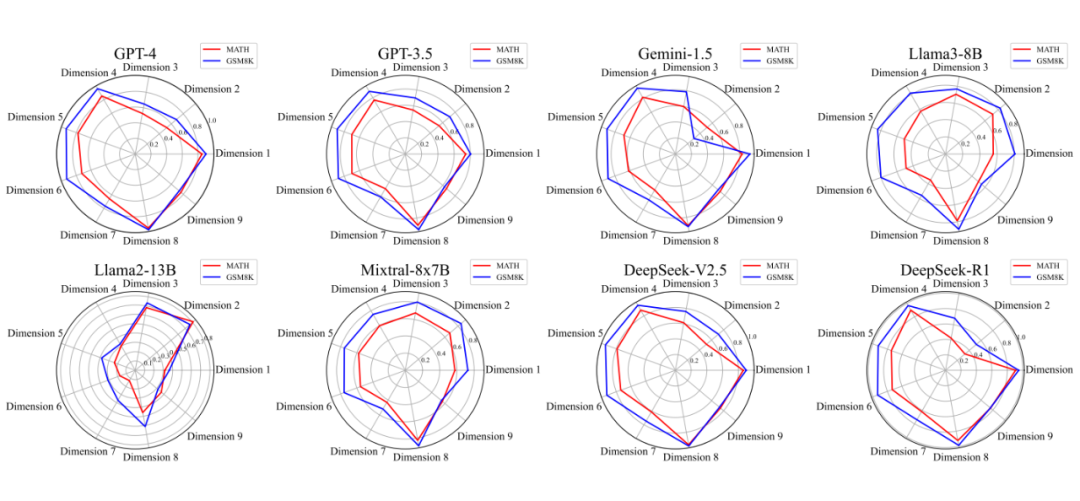
▲ 图2. CogMath 不同认知维度的评估结果
结论3:模型对知识的掌握更多是“死记硬背”
图 2 中,GPT-4、DeepSeek 等模型在“问题求解”阶段中维度 7 的通过率最低,这说明当前模型尚不能将知识融入推理链中,而是机械套用。
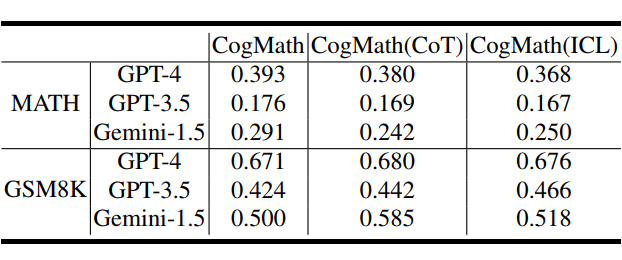
▲ 表6. CoT、ICL 对评估结果的影响
结论4:CoT与ICL并不能从本质上提高数学能力
如表 6 所示,在 MATH 数据集上,我们的 CogMath 评估框架揭示出思维链(CoT)与上下文学习(ICL)均导致性能下降(例如 GPT-3.5 从 0.176 降至0.169),而在 GSM8K 上则带来小幅提升(如 Gemini-1.5 从 0.500 提升至 0.585)。
这表明这些方法在处理简单任务时能够帮助模型更好地组织思路,但在面对需要更高阶逻辑的复杂任务时,其效果十分有限。因此,这类方法本质上仍是“辅助性工具”,难以从根本上提升模型的数学推理能力。

展望未来:对齐人类认知的数学评估框架
在当下 AI 大模型效果横行、层出不穷的时代,我们应该超越表面指标,深入讨论这些系统的本质认知能力,探寻它们与人类推理过程的异同与偏差。
CogMath 提出的多维评估体系不仅适用于数学任务,也可自然扩展至更广泛的认知任务。作为一种基于推理过程的多维评估方法,CogMath 不仅像一台“认知显微镜”,精准解析大模型的数学能力,还体现出对人类认知过程的深度对齐,为推动大模型向更加科学、可信的方向演进提供了有力支撑。
(文:PaperWeekly)

