
近年来,大语言模型(LLMs)的发展正经历一个重要转变:从快速、直觉式反应的“系统 1”思维,迈向具备反思和纠错能力的“系统 2”式深思熟虑。
然而,现有的大部分评测基准只关注最终答案的准确率,忽视了模型在推理过程中的中间步骤,因而无法有效评估模型自我反思、发现并纠正错误的能力。
为了弥补这一差距,来自达摩院和新加坡南洋理工大学的研究团队提出了 FineReason,一个基于逻辑谜题的基准,旨在系统性地评估和提升大模型的审慎推理(deliberate reasoning)能力。
另外,通过在解谜数据上训练,模型在数学以及通用推理任务上的准确率实现了高达 5.1% 的提升,证明了教模型“解谜”能有效增强其通用“解题”能力。

论文标题:
FINEREASON: Evaluating and Improving LLMs’ Deliberate Reasoning through Reflective Puzzle Solving
论文链接:
https://arxiv.org/abs/2502.20238
代码链接:
https://github.com/DAMO-NLP-SG/FineReason
现存问题及挑战:只看结果,不问过程
在认知科学中,人类的思维被分为两个系统:系统 1 快速、自动,如同直觉;系统 2 则缓慢、费力,负责逻辑分析1。当前,我们希望 LLMs 也能掌握强大的系统 2 能力,以解决更复杂的任务。
评测层面上,主流的数学和编程基准大多只关心模型最终输出的答案2,3,4,5。模型可能从错误的推理路径得出了正确答案。这不仅让我们无法信任模型的推理过程,也阻碍了我们深入理解和改进其核心推理机制。
训练层面上,这些领域的推理数据不仅普遍缺乏对中间步骤的标注,而且标注过程本身也极其困难。一个数学题或代码任务可能有多种有效的解题路径,如何判断每一步的对错需要大量的专家知识。这种标注的缺失和困难,导致我们难以训练过程奖励模型(process reward models)来引导模型步步推理。
用“解谜”量化思考过程
为此,我们引入了 FineReason, 涵盖四种逻辑谜题:数独、24 点、图着色、逻辑网格谜题。
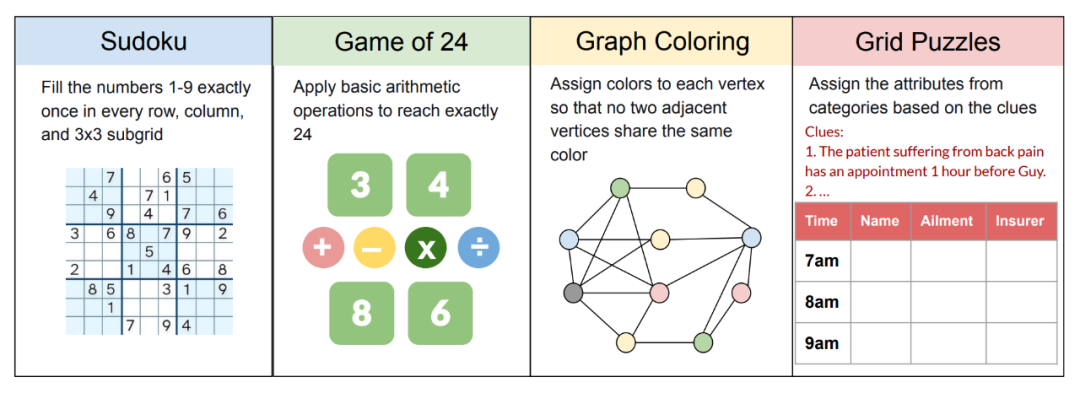
选择逻辑谜题的原因在于其独特的优势:
-
过程可分解:解谜过程可以被拆解为一系列子步骤。
-
规则明确:每一步的正确性都可以依据规则自动验证,解决了传统推理任务中标注难的问题。
我们设计了两项评测任务,以精细化地评估模型的系统 2 推理能力:
-
状态检查 (State Checking):模型判断当前解题状态是否能达到可解答案,以衡量模型的反思和前瞻能力。
-
状态转移 (State Transition):模型在给定状态下,给出下一步操作,以考察模型的行动规划和回溯纠错能力。
以解数独为例,一个数独可以分解为多个子步骤,模型需要不断地判断当前步骤是否违反数独规则,预判未来步骤是否可解,以及决定继续填数或者移除数字。
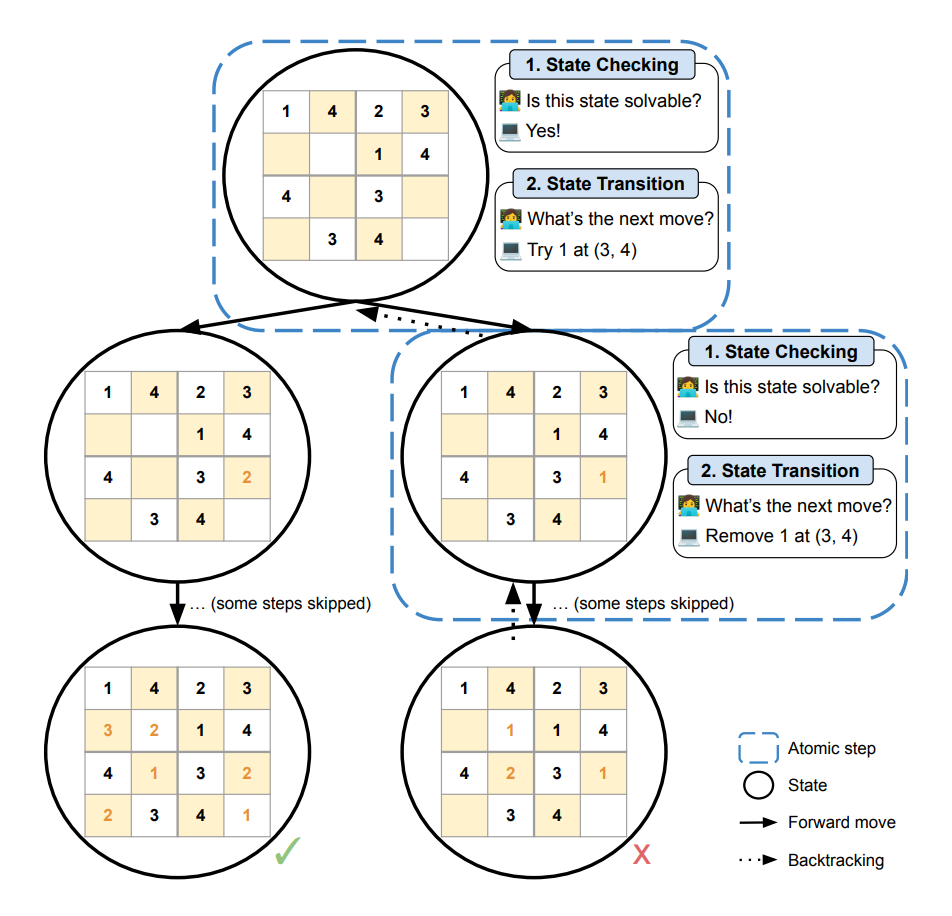
我们通过 depth first search 构建完整的解题树,从而自动生成全部状态以及标签。(详情见论文)
主要发现
1. 顶尖推理模型间的隐藏差异
在传统基准上,顶尖的推理模型(如 Gemini-2.0-Flash-Thinking 和 o1)表现得不相上下。但在我们的基准中,能看出 Gemini 在 State Transition 任务上明显落后于 o1:
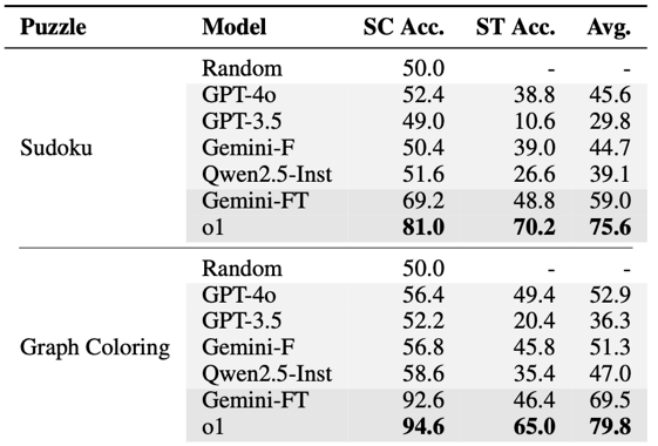
这表明,FineReason 能够捕捉到其他基准忽视的、模型在动态决策和纠错能力上的细微但至关重要的差距。
2. 模型普遍擅长判断,却不擅长行动
模型在 State Checking 任务上远比 State Transition 好。这意味着模型能大致判断出“这条路看起来能走通”,但当被要求“具体走出下一步”,就无法正确回答。
3. 真正的瓶颈:不是“犯规”,而是“迷路”后不知回头
我们进一步深入分析了模型在 State Transition 中的表现:
a) 模型处理 solvable states 的能力远超于处理 unsolvable states。这表明,模型沿着正确的道路前进相对容易,但一旦进入死胡同,进行回溯就变得困难。
b) 较强的推理模型很少违反规则(invalid moves),比如在数独的同一行填入两个相同的数字。然而,几乎所有模型最常见的错误都是回溯失败(backtracking failure)。当它们意识到走错了路,却无法准确地退回到上一个正确的决策点,而是选择继续犯错,或者错误地跳到更早的步骤。
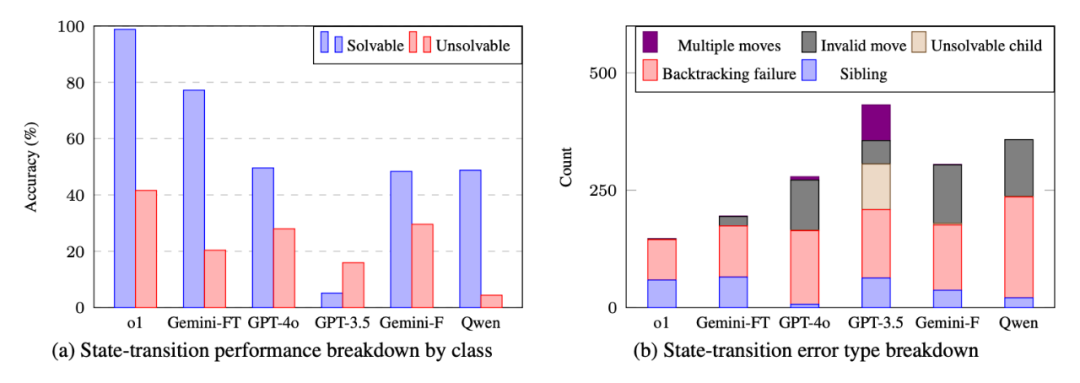
这些发现表明模型在实现真正“系统 2”推理时面临的核心障碍:它们缺乏反思与纠错的能力。
从“解谜”到“解题”,实现推理能力迁移
为了提升模型的反思与纠错能力,我们将谜题数据与数学推理数据混合,对模型进行 GRPO 训练。结果显示,经过谜题训练的模型在数学推理中均有提升:
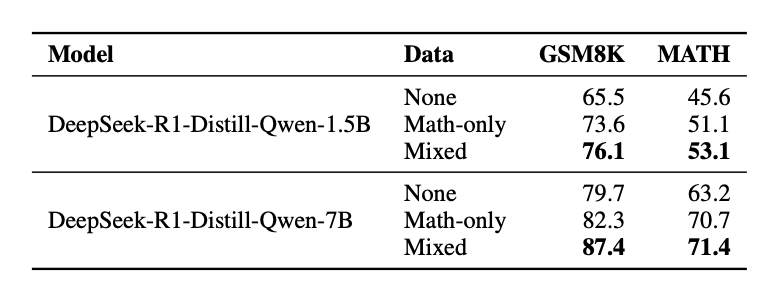
在多种通用推理任务上也有提升:
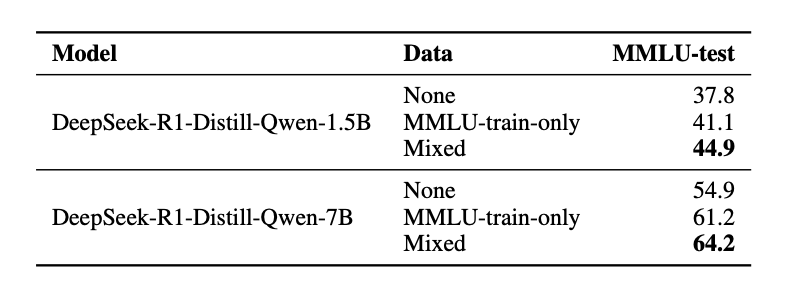
另外,我们对模型输出的质量分析也验证了,模型从解谜中学习到的核心推理技能如约束验证、试错、回溯和系统性探索,是可以成功迁移到其他领域的推理任务中。(详情见论文)
总结
FineReason 通过将解谜过程拆解为可自动验证的子步骤,并设计“状态检查”和“状态转移”任务,实现了对模型审慎推理能力,尤其是其反思和纠错能力的精细化量化与评估。
研究揭示,尽管顶尖模型表现卓越,但在动态决策和从错误中回溯的能力上仍存在显著瓶颈。此外,谜题数据集的训练显著提升了模型在通用推理任务上的表现。
未来,这项工作可以向更多维度扩展,例如探索更复杂的多模态谜题,或将这种谜题过程监督的训练方法应用到代码、科学等更广泛的领域,持续推动模型从“快速反应”向“深度思考”的进化。
参考文献
[1] Kahneman, D. (2011).Thinking, Fast and Slow. Farrar, Straus and Giroux.
[2] Hendrycks, D.,et al.(2021a). Measuring Massive Multitask Language Understanding. InInternational Conference on Learning Representations.
[3] Cobbe, K.,et al.(2021). Training Verifiers to Solve Math Word Problems.arXiv preprint arXiv:2110.14168.
[4] Chen, M.,et al.(2021). Evaluating Large Language Models Trained on Code.arXiv preprint arXiv:2107.03374.
[5] Hendrycks, D.,et al.(2021b). Measuring Mathematical Problem Solving with the MATH Dataset. InThirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2).
(文:机器学习算法与自然语言处理)

