作为第一作者，想从idea来源的视角介绍一下这个工作。在知乎潜水多年，首答就献给这个问题了。答得不好的地方请大家多多批评指正（鞠躬）。非常感谢刘忠鑫老师和 Binyuan Hui 老师的指导，以及所有合作者的帮助，尤其感谢通义千问的资源支持。

论文名称：Parallel Scaling Law for Language Models
论文链接：https://arxiv.org/abs/2505.10475
代码：https://github.com/QwenLM/ParScale

我们都知道，除了拓展数据量以外，现在有两条主流的 scaling 路线来增强拉大模型的计算量，增强大模型的能力：

• • 扩展参数：非常吃显存
• • 扩展推理计算量：主流方法都是增大思维链长度，非常吃时间，并且依赖于训练数据、训练策略（RL），只适用于部分场景。

那么问题来了：能不能有一种新的 scaling 路线，不会带来显著的内存和时延增加，同时又适用于一切的场景？

我们的核心想法就是：在参数量不变的情况下，同时拉大训练和推理并行计算量。

动机由来

最初其实是舍友在宿舍学习 diffusion 模型，他对 diffusion model 必用的一个 trick 百思不得其解：Classifier-Free Guidance（CFG）。CFG 在推理阶段拿到输入 x 时，首先做一次正常的 forward 得到 f(x)；然后再对 x 进行主动的劣化（比如去除条件）变为 x’，再进行一次 forward 得到 f(x’)。最终的输出 g(x) 是 f(x) 和 f(x’) 的一个加权组合，它的效果比 f(x) 更好，更能遵循输入的条件。

这个现象事实上有点反直觉：f(x) 和训练阶段是对齐的，而 g(x) 明显和训练阶段的目标存在 gap。按照常识，只有训练目标和推理目标形式相同，推理才能发挥最大效果。另外，f(x) 的参数量和 g(x) 也是相同的，输入的有效信息量也相同，为什么 f(x) 反而学不到 g(x) 的能力？这说明背后或许存在更深层次的原因。

我们做出了大胆的猜想：CFG 生效的原因，本质上是用了双倍的并行计算量，它拉大了模型本身的 capacity。

这就启发我们，可以进一步 scale：

• • 把输入的变换形式（比如人为设计的劣化规则）和输出的聚合规则变成可学习的
• • 拉大并行的数目

这个方法非常简单，可以应用到任何的模型架构、任务和数据上。我们在大语言模型上首先探索了这一想法，如下图所示：

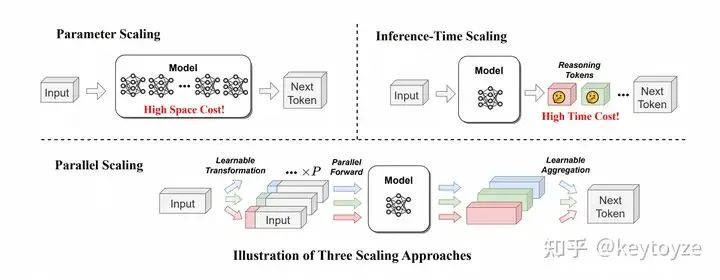
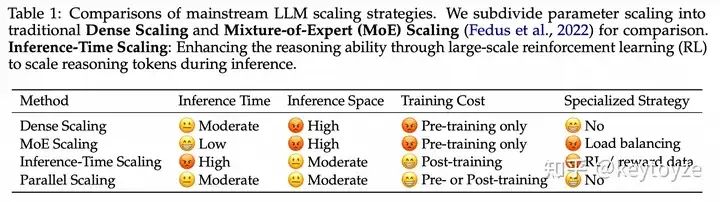
Parallel Scaling Law

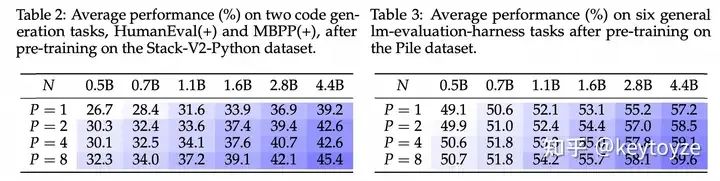
我们首先进行了一系列理论分析，得出一个结论：将一个参数量为 N 的模型并行 P 个流，等价于将参数量变为原来的  倍（详见论文的分析）。其中 Diversity 与不同流之间的残差相关系数有关，不好接着分析。但这至少说明，放缩并行计算量和放缩参数之间必然存在着某个联系

因此，我们接下去做了大量的实验，最终得到：并行P个流，等价于把参数放大O(logP)倍，但它相较于放大参数有着非常显著的推理效率优势：

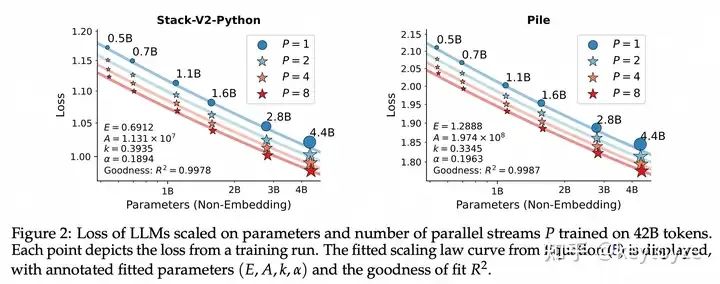
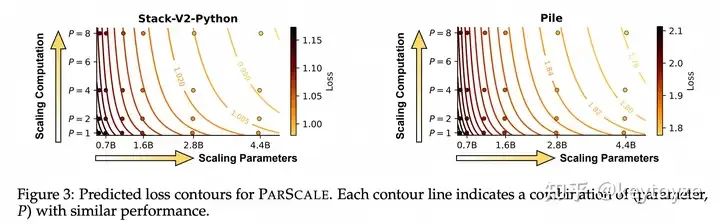
我们也提供了一个 HuggingFace 空间，来更直观地感受 Scaling Law 的力量。欢迎大家试用：

https://huggingface.co/spaces/ParScale/Parallel_Scaling_Law

两阶段训练

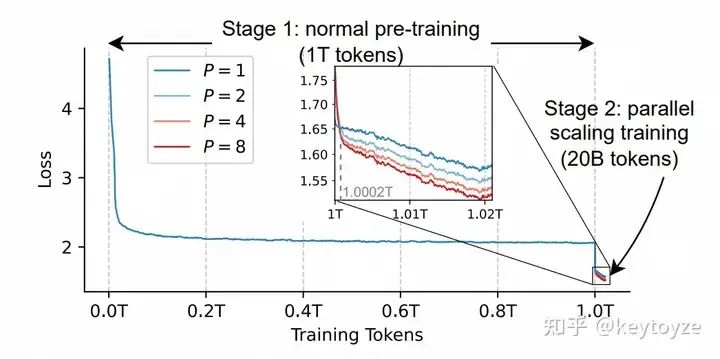
先前的实验主要聚焦在 pre-train，由于 batchsize 会拉大 P 倍，训练开销较大。因此我们尝试了一个后训练策略：首先第一阶段训练 1T token（常数学习率），然后在二阶段使用 ParScale（退火学习率）后训练 20B token。可以发现这个策略也是非常有效的。

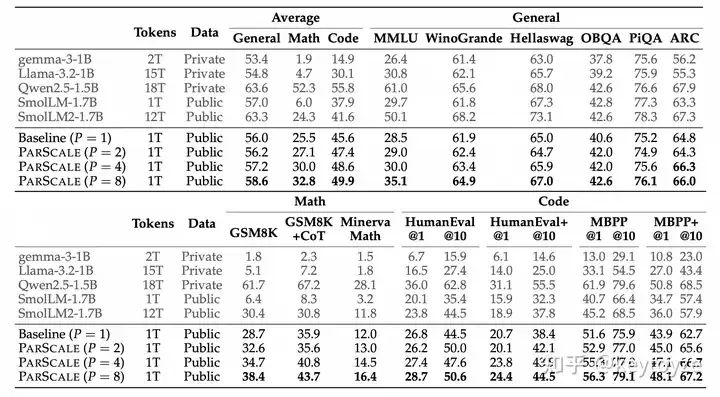
之后，我们将 ParScale 应用到 Qwen-2.5 模型上（已经训了 12 T token），包括全参数持续训练（CPT）和 PEFT 训练（冻结主网络，只微调引入的 prefix 参数）。

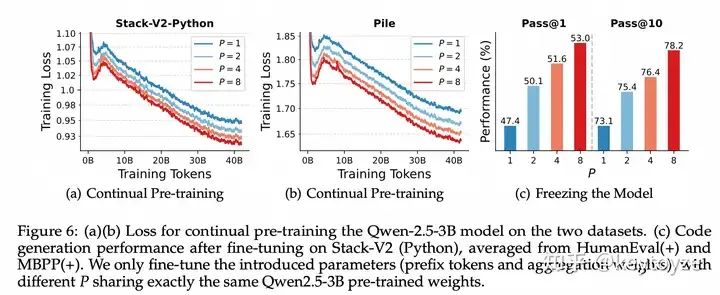
值得一提的是，PEFT 训练展示出了动态并行拓展的前景：我们可以使用相同的模型权重，在不同的场合下使用不同的 P，从而快速地动态调整能力以及推理开销。这是目前的主流方法比较难做到的。

总结

ParScale 是我们探索 LLM Scaling Law 的新尝试，目前的研究仍然在进行中。我们相信扩展计算量可以带来智能的涌现。展望未来，我们计划进一步在更多的模型架构（比如MoE）以及更大的数据上进行尝试，从而更好地理解扩大并行计算能带来的收益。更多的未来方向讨论详见论文。欢迎大家多多批评指正！