研究背景
机器学习模型在诸多领域已经取得了显著的成功,例如图像识别、自然语言处理和自动驾驶等。然而,许多机器学习算法依赖于一个限制性极强的假设,即训练数据和测试数据的分布是相似的。
这一假设在现实场景中往往难以成立,例如由于环境变化、传感器差异或数据采集条件的不同,测试数据分布可能与训练数据分布存在显著差异,导致模型性能下降。
测试时适应方法(Test-time Adaptation, TTA)旨在通过在测试阶段调整模型来减轻数据分布差异带来的负面影响。熵最小化(EM)已被证明是现有测试时自适应(TTA)方法中简单而有效的基石,绝大多数的现有方法都基于熵最小化这一无监督信号展开。
传统的熵最小化(EM)方法虽然简单高效,但存在严重缺陷:
1. 过度自信问题:EM 强制模型对所有测试样本输出低熵预测,导致对错误分类或异常样本的置信度过高。
2. 模型崩溃风险:在不可靠样本上持续优化熵,可能使模型参数漂移至无效解,性能急剧下降。
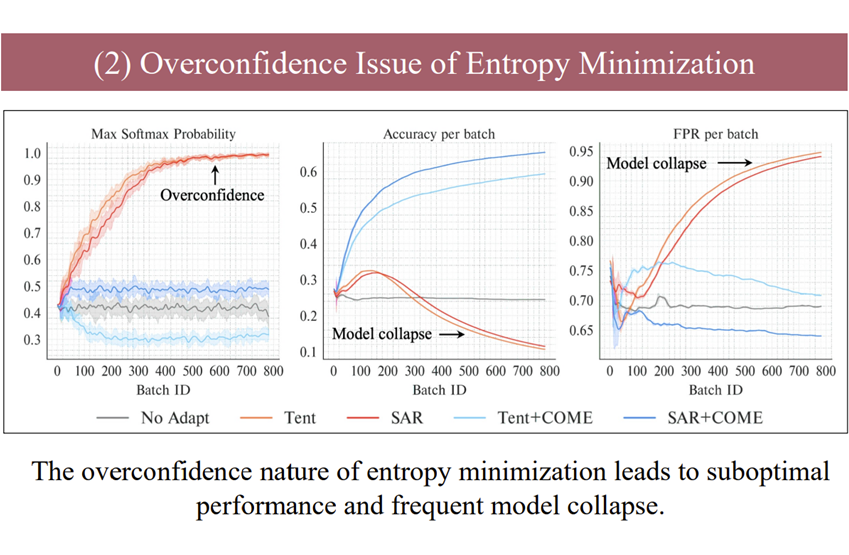
如上图所示,我们研究了熵最小化(Entropy Minimization, EM)在 TTA 场景下对两种代表性方法的影响,即 Tent(Wang et al., 2021)和 SAR(Niu et al., 2023)。
左图中可见,在逐个 epoch 的 TTA 过程中,Tent 方法和 SAR 方法都会持续地增强预测的信心,max softmax probability 值持续走高,出现模型过度自信预测的情况。
中图中可见,从第 200 个 epoch 开始,在模型过度自信预测的同时,模型出现了预测准确率大幅下降的情况,我们把这种情况称作模型崩溃;从右图中的假阳性率的走势也可以看出,在模型过度自信预测的同时,模型几乎丧失了分类预测的能力。

方法
ICLR 2025 上发表的论文 COME: Test-time adaption by Conservatively Minimizing Entropy 提出了一种保守的熵最小化方法,能够解决熵最小化导致的模型崩溃问题。

论文标题:
COME: Test-time adaption by Conservatively Minimizing Entropy
收录会议:
ICLR 2025
论文链接:
https://arxiv.org/abs/2410.10894
GitHub链接:
https://github.com/BlueWhaleLab/COME
COME 的核心创新在于显式建模预测不确定性,并通过自适应正则化防止过度自信。具体方法如下。
2.1 基于主观逻辑的不确定性建模(解决过度自信问题)

问题:传统 softmax 输出无法区分“不确定”和“错误”的预测,导致模型对异常样本依然高置信度。
方法:引入主观逻辑(Subjective Logic),将模型输出转换为 Dirichlet 分布,生成:
-
类别置信量(belief mass):对每个类别的支持证据。
-
不确定性量(uncertainty mass):反映模型对当前样本的总体不确定性。
效果:模型可以明确表达“我不知道”,避免对不可靠样本强行给出高置信度预测。
2.2 保守熵最小化目标(解决模型崩溃问题)

问题:直接最小化熵会迫使模型对所有样本降低不确定性,包括噪声和离群值。
方法:优化主观意见的熵(而非 softmax 熵),并约束不确定性质量不偏离预训练模型的初始估计:

2.3 自适应 Logit 约束(实现高效正则化)
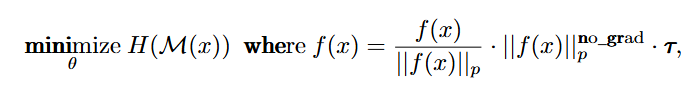
问题:直接约束不确定性需要存储预训练模型状态,增加计算开销。
方法:通过冻结 Logit 范数(即 )间接控制不确定性:
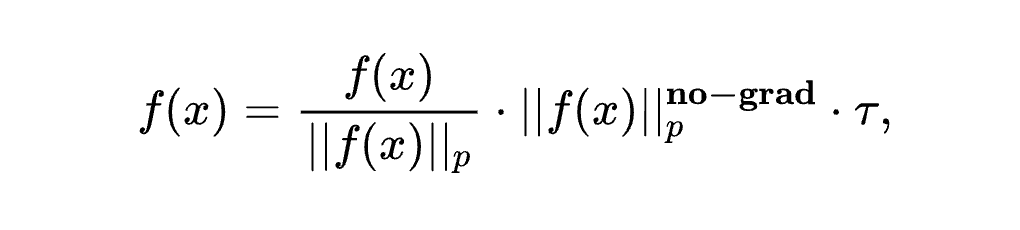
效果:无需额外存储,单次前向传播即可实现稳定优化,满足 TTA 的实时性要求。

COME 无需修改模型架构或训练策略,仅需几行代码即可嵌入现有 TTA 方法,是一种轻量级、模型无关的解决方案。

实验结果
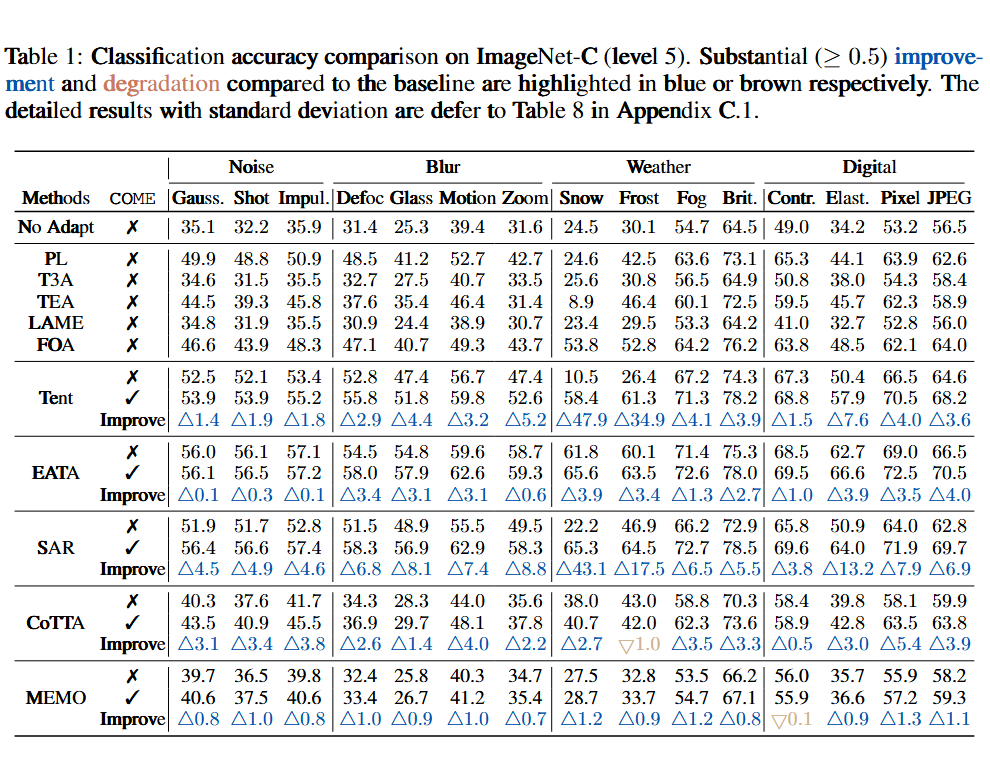
我们在 Imagenet-C(level 5)数据集上进行了对比试验
COME 在多种复杂场景中均显著优于传统方法:
标准 TTA(ImageNet-C):
-
COME 是一种对熵最小化的改进,直接用于基于熵最小化的方法上,均能显著提高模型预测能力。
-
在 Snow 噪声(Level 5)下,分类准确率提升 47.9%(Tent+COME vs. Tent)。
-
在 15 类混合损坏数据上,平均准确率提升 9.0%(SAR+COME vs. SAR)。
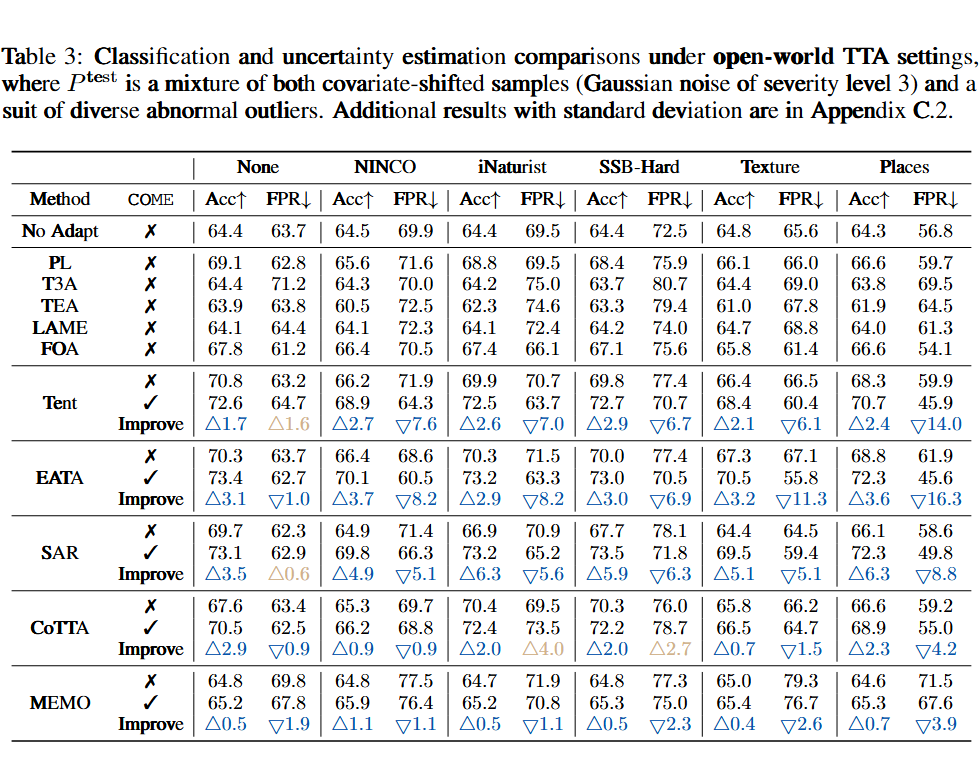
开放世界 TTA(含异常样本):
-
在开放世界的实验设定下,模型会遇到 outliers 数据,在这种设定下 COME 也能对原方法有显著提升。
-
假阳性率(FPR)降低 14.5%(NINCO 数据集),显著减少对离群样本的误判。
终身学习TTA(持续分布变化):在动态数据流中,COME 也能够保持稳定性能。

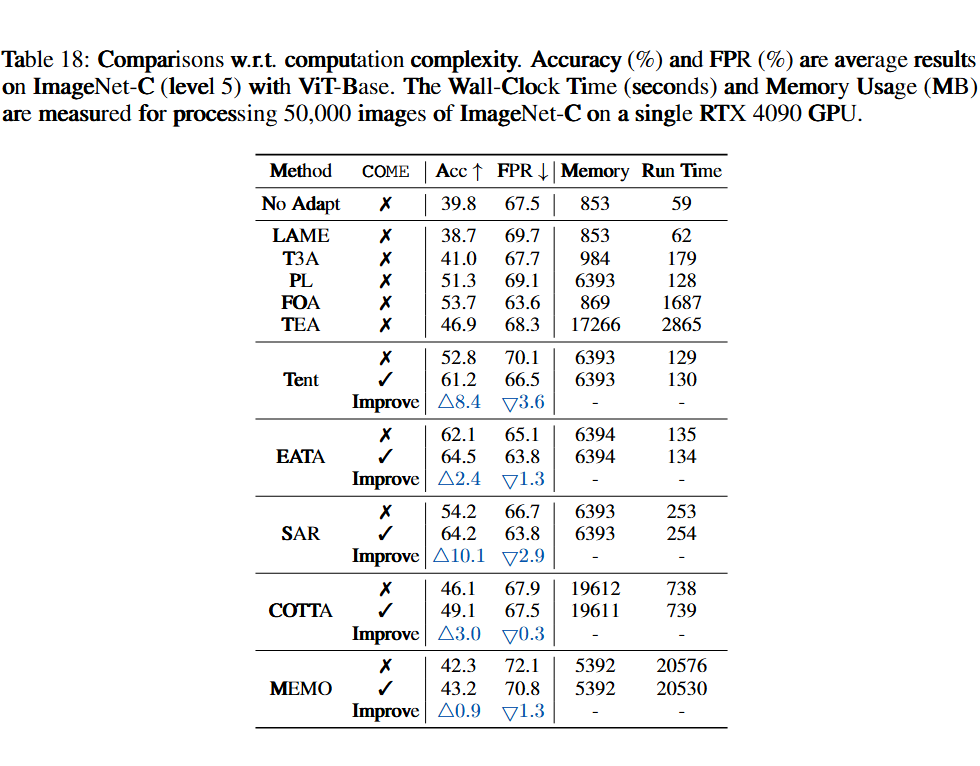
计算效率:相比不使用 COME 的原方法相比,COME 仅增加 <1% 的推理耗时,适合实时部署。

总结
COME 通过显式不确定性建模和自适应熵优化,解决了 TTA 中的两大核心问题:
1. 过度自信 → 通过 Dirichlet 分布量化不确定性,避免对噪声样本盲目自信。
2. 模型崩溃 → 约束不确定性质量,防止优化过程破坏预训练知识。
代码已开源,欢迎访问 GitHub 探索如何用 5 行代码提升您的 TTA 模型鲁棒性!
https://github.com/BlueWhalelLab/COME
(文:PaperWeekly)