
©作者 | 朱贝尔、王若禹
单位 | NTU、西湖大学
研究方向 | 机器学习、扩散模型
近年来,扩散模型(Diffusion Models)凭借出色的生成质量,迅速成为图像、视频、语音、3D 内容等生成任务中的主流技术。
从文本生成图像(如 Stable Diffusion),到高质量人脸合成、音频生成,再到三维形状建模,扩散模型正在广泛应用于游戏、虚拟现实、数字内容创作、广告设计、医学影像以及新兴的 AI 原生生产工具中。
其背后的核心机制是「逐步去噪」过程:从一张完全随机的图开始,模型通过上百次迭代逐步还原出清晰、真实的图像。这种逐步精化的策略虽然保证了生成质量,却也带来了显著的推理延迟,成为制约其部署效率的瓶颈,尤其在移动设备、实时生成和大规模应用中表现尤为明显。
为了解决这一问题,研究者提出了三种主要的加速思路:一是通过数值求解器(ODE Solvers)减少迭代步数;二是采用模型蒸馏(Distillation)将多步过程压缩为少步甚至一步;三是借助并行计算(Parallelism)加速多个计算路径的推理。
然而,每种方法都存在局限:数值求解器在迭代步数极少时往往会损失生成质量;蒸馏方法则需重新训练模型,成本高昂;并行方法虽具潜力,但在低步数场景下仍未被充分挖掘。
为此,西湖大学 AGI 实验室提出了一种融合三类优势的创新方案——Ensemble Parallel Direction Solver(EPD-Solver)。该方法以数值求解器为骨架,通过轻量级蒸馏学习获得少量可学习参数,并在每次迭代中并行计算多个方向的梯度,再以加权方式融合,从而有效减少数值积分误差。
这种方式不仅无需对模型进行大规模改动,也不会带来额外的延迟开销,成功实现在 3–5 步采样下仍能生成高质量图像。
更进一步,EPD-Solver 还能以「插件」的形式应用于现有的主流求解器中,显著提升其生成质量和效率。
大量实验表明,在相同计算延迟下,该方法在 CIFAR-10、FFHQ、ImageNet 等多个基准测试中取得了领先的图像生成效果,展示出其在低延迟高质量生成任务中的巨大潜力。

论文标题:
Distilling Parallel Gradients for Fast ODE Solvers of Diffusion Models
论文链接:
https://arxiv.org/abs/2507.14797
代码链接:
https://github.com/BeierZhu/EPD

动机
从宏观层面来看,各类 ODE 求解器都在「如何利用有限的梯度估计去近似积分」上下功夫,如下图所示:
-
DDIM 只利用起点梯度()近似积分;
-
EDM 利用梯形法,利用起点梯度()和终点梯度()近似积分;
-
AMED 通过轻量网络预测一个中间时刻 ,利用该时刻 梯度近似积分。
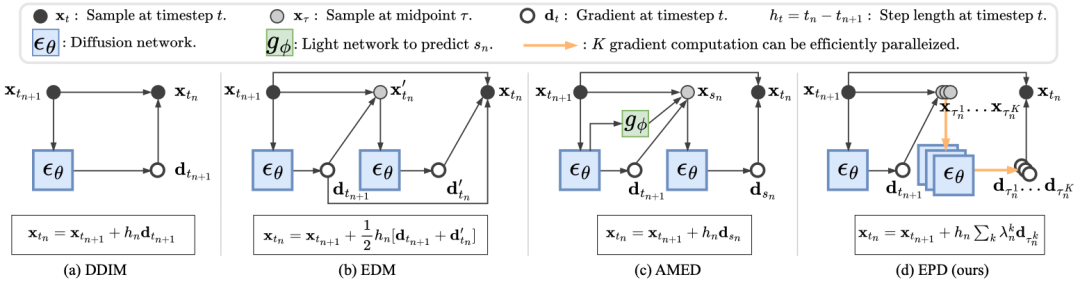
EDM 和 AMED 在 DDIM 的基础上,增加了一次额外梯度评估( 与 )来提升积分近似精度。该方法的核心动机是将额外梯度评估扩展到多个时刻,提出 EPD-Solver:
-
并行计算 K 个中间时刻的梯度()
-
凸组合融合 K 个梯度,获得更精确的积分近似()
-
由于所有梯度互相独立,不增加整体采样延迟
理论支撑(Mean value theorem for vector-valued functions)
对于在闭区间 上连续、在开区间 上可微的 维向量值函数 ,存在系数 和中间点 ,使得:
将其应用于去噪积分 ,即可等价地表示为「在若干中间时刻计算梯度并按简单形权重加权求和」,这正是 EPD-Solver 的核心思想。

方法
参数定义与更新
在每个采样步骤 n 中定义参数集 Θₙ = {τₙᵏ, λₙᵏ, δₙᵏ, oₙ}ₖ₌₁ᴷ,其中:
-
τₙᵏ ∈ (tₙ₊₁, tₙ):第 k 个中间时刻
-
λₙᵏ ≥ 0 且 ∑ₖ λₙᵏ = 1:梯度融合权重
-
δₙᵏ:中间时刻偏移量
-
oₙ:输出尺度扰动参数
推理更新规则
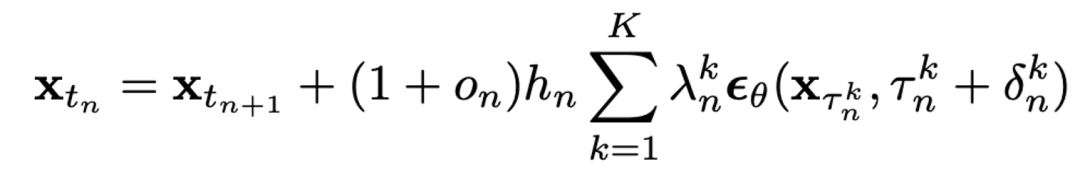
蒸馏训练流程
1. 教师轨迹生成:采用高精度 ODE 解算器(如 DPM-Solver)在扩展时间表 𝒯ₜₑₐ 上生成参考状态;
2. 学生轨迹采样:在相同初始噪声 下,使用学生时间表 𝒯ₛₜᵤ 采样得到学生状态;
3. 目标函数:针对每步 n,最小化学生与教师状态差异
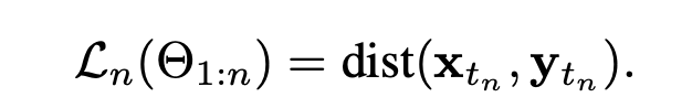
4. 端到端优化:通过 N 次反向传播,联合优化所有参数 Θ₁:ₙ
插件化集成
EPD‑Plugin 设计为可插拔模块,可无缝集成至现有多步 ODE 求解器(如 iPNDM)。用户仅需替换梯度计算与融合流程,即可在原框架下获得加速与质量提升。



实验结果
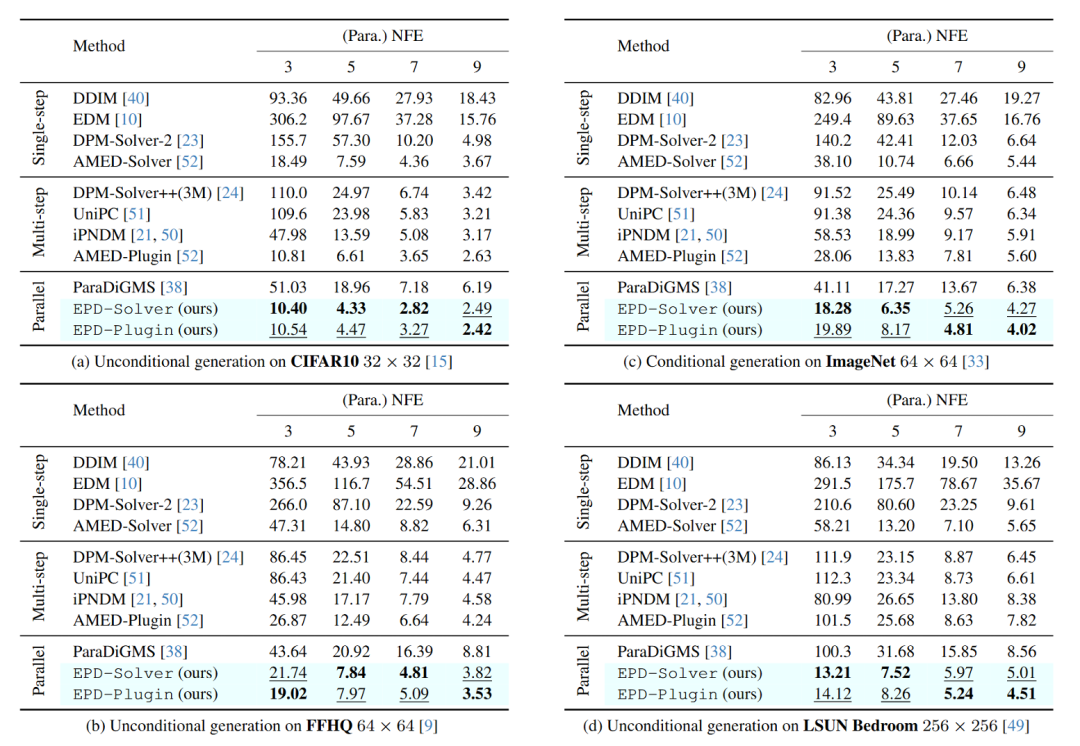
1. 性能全面领先:在 CIFAR-10、FFHQ、ImageNet 和 LSUN Bedroom 四个数据集的测试中,EPD-Solver (当 K=2 时) 在所有 NFE(函数求值次数)设置下,其 FID 分数均比基线求解器有持续且显著的提升。
2. 低 NFE 场景优势明显:在极低的 NFE 设置(例如 3 NFE)下,EPD-Solver 的优势尤为突出。例如,在 LSUN Bedroom 数据集上,EPD-Solver 的 FID 分数为 13.21,而次优的基线方法 AMED-Solver 的 FID 分数为 58.21。
3. 插件(Plugin)性能出色:当作为插件(EPD-Plugin)应用于 iPNDM 求解器时,该方法同样表现出色。尤其是在 NFE 大于 7 的场景,其性能普遍优于 EPD-Solver。
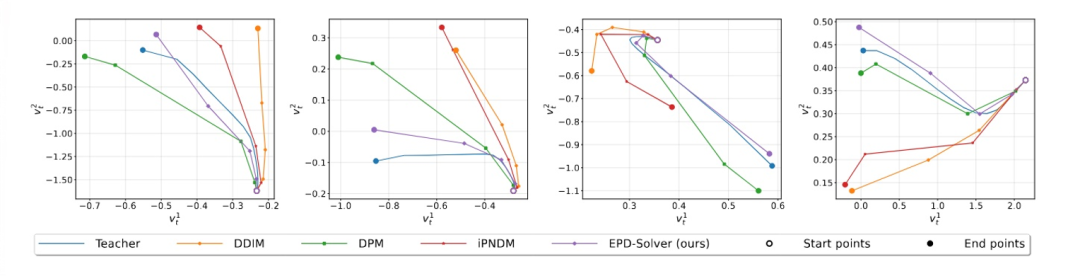
通过可视化两个随机像素在生成过程中的演变路径,可以观察到 EPD-Solver 的轨迹与「教师」轨迹展现出高度的一致性。相比之下,DDIM、DPM-Solver 和 iPNDM 等其他求解器的轨迹相比教师轨迹明显偏离。

在 Stable Diffusion v1.5 模型上,EPD-Solver 通过在极低的采样步数下(如 8-20 NFE)生成质量远超 DPM-Solver++(2M) 和 AMED-Plugin 等先进求解器,从而展现出显著的加速效果。

结语
通过 EPD-Solver,西湖大学的研究人员展示了如何利用其创新的并行梯度评估机制,在不增加单步推理延迟的前提下,高效且精确地减小了生图模型每步采样的截断误差,缓解扩散模型在低步数采样下的图像质量退化问题。
该方法的核心优势在于两点:
1. 并行效率与精度提升:通过引入多个可学习的中间时间步梯度评估并将其进行凸组合加权,显著提升了 ODE 积分近似的精度,从而降低了局部截断误差。尤为关键的是,这些额外的梯度计算因其独立性,可实现完全并行化,在保持单步推理零延迟增加的前提下提升了生成质量。
2. 训练轻量与即插即用:仅需通过蒸馏方式优化一个极小规模的可学习参数集,避免了代价高昂的扩散模型重训练或微调。该方法还可作为 EPD-Plugin 轻松集成至现有 ODE 采样器(如 iPNDM),进一步扩展其应用范围。
综上,EPD-Solver 突破了扩散模型在低延迟采样时速度与图像质量的核心权衡瓶颈,提供了一种高效、实用且易于部署的新方法。其在多个图像生成基准上显著优于现有先进求解器的实验表现,有力证明了并行计算是推动扩散模型高效采样发展的一个极具潜力的研究方向。
(文:PaperWeekly)

