TL;DR
本文主要介绍逆强化学习的算法原理, 讲解如何从专家数据中找到一个奖励函数来解释专家行为。由于逆强化学习算法众多,全面的介绍所有算法超出了本文的范畴。本文主要介绍基于以IQ-Learn为代表的最大边际逆强化学习算法。并在最后介绍基于IQ-Learn思想的南大的工作 《Generalist Reward Models: Found Inside Large Language Models》 (下文简称GRM)。本文的主要内容如下:
-
• 什么是逆强化学习? -
• 如何求解逆强化学习? -
• 最大边际逆强化学习 -
• 模仿学习是分布匹配问题,而逆强化学习与模仿学习互为对偶问题 -
• IQ-Learn -
• GRM
什么是逆强化学习?
强化学习(Reinforcement Learning, RL) 是给定交互环境与奖励函数 后求解一个最优策略 使得最大化期望累积奖励, 并生成优质轨迹。
而逆强化学习(Inverse Reinforcement Learning, IRL) 则是反其道行之:假设我们有一批采集于专家策略 的离线轨迹数据 , 我们希望找到一个奖励函数 来解释数据中的行为。即认为专家策略 的生成是通过一个内在奖励函数 得到的。
如何求解逆强化学习?
正如上述所说,逆强化学习希望从专家轨迹数据 中恢复奖励函数 。那么建立求解IRL范式的核心在于建立从奖励函数 到专家策略 的映射,从而通过专家数据求解反问题来恢复 。事实上,通过建立不同的 与 的关系,我们可以衍生出不同的IRL算法分支。下面便是两种具体分支(其他算法不再具体展开):
基于最优性条件建模
通常专家策略 采集到的数据是高质量的轨迹数据。因此这类方法直接认为专家策略实际上是以为奖励函数的最优策略. 给定任意奖励函数, 如果我们定义函数是以为奖励函数运行RL得到的最优策略集合, 那么根据假设有.
从而IRL 求解的是逆问题,即给定 的数据后,我们希望求解 。因此这类算法的一个核心在于如何利用MDP的最优性条件来恢复 。
-
• 一种是通过线性规划来直接建模 在 下的MDP的在最优性 [1], -
• 一种则是本文所讲的最大边际算法, 最大化 的值函数与其他策略的值函数的差距来建立最优性。
直接概率建模
这类方法以最大熵逆强化学习[3]为代表, 直接通过奖励函数 建模了 。以确定性环境为例,给定轨迹
该算法认为专家策略 对应的轨迹概率 满足:
且专家数据 . 因此我们可以通过例如极大似然估计与Bayes等方法来估计 .
最大边际逆强化学习
基于最大边际IRL算法最早出现在 2004年的吴恩达的工作 [2], 其基本求解范式如下:
其中 是给定奖励函数下专家策略的值函数与 实际最优策略的值函数的差(即边际),是奖励函数空间,是给定奖励函数下策略在初状态分布 下的期望累积奖励,即:
为什么最大边际算法是合理的?
如果我们仔细看一下边际 在不同奖励函数 上的取值便可知其合理性。 我们把奖励函数 分成两类。第一类是使得 成为最优策略的奖励函数集合 , 即,
另一类则是没有使得 成为环境最优策略的奖励函数集合, . 根据定义我们容易知道:
因此通过求解最大边际目标函数得到的奖励函数, 必然使得,从而能够使得专家策略成为环境的最优策略,这满足我们对真实的专家奖励的假设: 即是专家奖励 上的最优策略。
如何求解最大边际IRL?
如果我们仔细观察 求解目标 (1) 的式子可以发现,要求解 ,我们需要对每一个固定的奖励函数 , 求解出专家值函数 与 最优值函数 。
实际上,前者是可以直接从专家轨迹数据中估计出来,而后者需要求解一个RL问题,如果不进行近似或化简,整个问题是intractable的。 实际上围绕如何化简求解 衍生出了不同工作。
本文后面所讲的IQ-Learn的一个非常重大的贡献则是利用了Inverse Bellman Operator 直接得到了最优策略与最优值函数,从而将嵌套优化变成了单目标优化。下面我们仍然以最早期的2004年的吴恩达的工作 [2] 为例,来直观的感受下IRL的一种求解方式,怎么将整个问题变成tractable的。
我们考虑离散的状态空间 与动作空间 。假设每个状态 有一个特征向量 , 我们建模奖励函数为参数 与特征向量的内积,且只与状态有关, 即:
根据我们在 (2) 中的值函数定义, 对任意参数 与策略 , 我们有值函数
其中
为feature expectations. 因此给定专家轨迹数据集
对于任意参数奖励函数参数 , 我们都可以通过 得到专家值函数的估计:
主要到求解目标(1) 还需要对每个 知道。在[2] 中,为了使得这一项变得tractable, 算法过程会迭代收集策略,得到一个策略集合,并通过近似得到。 具体来说,考虑第次迭代步数 , 假设我们已经有一个策略集合(当 k= 0的时候随机初始化一个策略) 与对应的 feature expectations 的估计, 那么给定任意的参数向量 , 我们有
从而最大边际IRL目标函数(1) 更新新的参数 近似变成了下面问题:
可以看到上述目标函数对于 来说是线性的,易处理的。当我们得到 后,我们运行 RL算法求解基于 上的最优策略 并加入策略池子。再开始新的迭代。在原始论文中,我们对边际做阈值控制,来判断什么时候停止算法。原始论文中的算法步骤如下:

正则下的最大边际IRL范式
回顾最早期工作 [2]中提出的最大边际IRL范式
我们在前文中论证了该范式的合理性,并以[2]为例讲解了一个实际的求解算法。然而该范式在提出后,求解是十分困难的。为了增加该范式的可求解性与鲁棒性,后续工作为该范式添加了正则化约束,来保证该问题更易求解的。为了方便论述,我们首先增加一些符号的定义。我们仍然考虑离散的状态空间 与动作空间 。我们定义 状态动作对 在整个轨迹中的的折扣访问概率为:
那么容易验证 (2) 中的值函数定义满足 :
是奖励向量 与访问概率向量 的内积。从而最大边际IRL目标 (1) 等价于
我们容易注意到, 整个问题关于 和 都是线性的。给定一个 ,内层关于 的求解可能有多个最优策略,同样外层的 也有可能有多个最优解。因此在 最大熵相关工作[3,5] 后, 后续的工作对内外层分别添加了正则化元素,保证整个问题是一个(strongly) concave-convex, 于是可以通过对偶等理论,简化整个问题。具体来说,有两个改动:
-
• 考虑最大边际熵正则下的值函数. 我们定义
即 是奖励函数 下,熵正则系数为 的策略 的值函数。容易验证:
考虑熵增则值函数的一个非常大的好处是,最优策略有且只有一个. 后续工作如IQ-Learn 则充分利用了这一点
-
• 对奖励函数 添加一个concave的正则项 , 其中 是一个convex函数. 如果 是strongly convex, 那么我们可以保证求解的 是唯一的。
于是在这两个改动下,最大边际IRL目标(1) 变成了
可以看到原始的最大边际 IRL (1) 的解 是正则后的目标 (5) 中 取 的情况。注意问题(5)中有一个常数项,不影响最优性。因此为了符号上的简单,我们下面的论述都将它去掉。因此正则后的最大边际IRL为求解下面双变量函数熵的max-min 问题
在 GAIL的工作 [6] 中, 对上述函数的max-min求解做了更深入的分析 (基于了[4]中有关访问概率的一些分析),在下一节中会介绍主要的结论。如果不感兴趣的同学可以直接跳到下下节中有关IQ-Learn的介绍。
模仿学习与逆强化学习的内在关系
这一节,我们会介绍 GAIL[6] 中对正则下的最大边际IRL目标 (5) 的一些理论分析,最终揭示模仿学习和逆强化学习的内在关系。 我们考虑奖励向量来自于整个实数空间, 即 . 下面我们逐步说明:
-
• 对目标函数 的求解,可以在访问概率空间进行,而不是策略空间 进行。同时函数 关于 在 -
• 我们说明目标函数 是max-min可交换的。在 强凸下存在唯一最优值点 -
• 模仿学习本质上分布匹配问题 -
• 正则下的IRL问题在max-min交互后得到的对偶问题是分布匹配问题, 从而说明模仿学习与逆强化学习互为对偶问题。
Bellman Flow Constraint : 策略与访问概率是一一对应的
注意到我们的目标函数 变量是, 函数值依赖于与。关于 的单调性与凹凸性未知,这就带来的分析的麻烦。好在,[4,9] 中指出了策略值与访问概率值的一一对应关系。我们定义多边形
其中 为转移概率。容易验证 是一个凸集。集合 中关于向量 的约束称为 Bellman Flow Constraints。我们定义策略 诱导出来的方位概率空间为
[4,9] 指出,如果我们把访问概率 看成一个关于的映射,那么实际是从到的一一映射。即, 并且不同的有不同的。更具体的,给定中的任意一个向量 , 我们可以构造诱导出的策略
可以证明 的访问概率向量为 本身,即 。从而同样可以得到 与 满足
正则下的IRL目标关于访问概率是强凸的
基于上面的观察,我们可以得到, 正则下的IRL目标函数 (6) 实际上可以写成
其中函数 为 的轨迹上的策略熵,即,
[6] 中严格证明了, 是 的强凹函数,因此 在 下是关于 的强凸函数
正则下的IRL目标是min-max 可交换的, 在 强凸下具有唯一的最优点
回顾上面的分析,我们可以得到 正则IRL的目标函数 (6), 即 ,对内层 的求 操作,可以等价的转化为对访问概率 的一个强凸函数的求min操作。我们记
于是正则IRL的求解问题(5), 满足
其中 (a) (c) 利用了上一节讨论的 实际上是从到中的一一映射,而(b)是利用了强对偶性,即是关于凸的,关于凹的. 注意到本来关于就是强凸的,因此在强凸下,同时也是关于强凹的,从而存在唯一的最优点,在一一映射下,也存在唯一的最优点
模仿学习本质上是分布匹配问题
在论述模仿学习与逆强化学习互为对偶问题前,我们首先论述模仿学习本质上是分布匹配问题。模仿学习的目标是在不知道真实的奖励函数下,单纯给定专家策略 的轨迹数据后,我希望学习到一个策略 使得两者的值函数相近,甚至后者超越专家策略。我们仍然考虑无正则下的值函数。回顾我们在(3)中对值函数的分解有:
如果我们假设奖励函数向量 是有界的,例如
可以看到,即使我们不知道真实的奖励函数 是什么,只要是有界的,那么我们都可以通过最小化,专家策略与当前策略 的访问概率分布距离,都可以使得值函数的差距变小。因此模仿学习的主要工作都集中在,如何通过专家的轨迹数据来优化当前的策略 的轨迹分布,从而逼近 的轨迹分布。例如GAIL[6]求解的问题实际上即为专家轨迹分布与当前轨迹分布的JS距离,即
逆强化学习是模仿学习的对偶问题
根据(7), 正则下的 IRL目标(5) 是max-min可交换的,即
在交换后右侧的对偶原问题中,固定一个策略 ,我们考虑内层最大化 的求解可以得到
其中 是 的共轭函数。 如果我们考虑 是一个常数函数,那么容易得到
于是交换后的 原问题实际上为:
即寻找一个策略 使得轨迹与专家策略的轨迹分布相同, 即 , 同时希望最大化 诱导出来的策略熵。 可以看到这实际上就是一个典型的分布匹配问题。 因此我们的正则下的IRL目标,即
实际上是上述分布匹配问题 的对偶问题
IQ-Learn : Inverse Soft-Q Learning for Imitation
下面我们介绍 2021年的工作 IQ-Learn,讲解这篇工作通过数学变换,将正则下的IRL目标(5) 变得tractable的。本文的讲解的方法与原文还不一样,但是本质的思想是一样的,且更容易方便理解。回顾目标(5), 我们希望最大化熵正则下的值函数的边际来求解IRL,即
该问题intractable的原因在于对于每个 你都需要知道对应的RL后的最优值函数
实际上,注意到我们的值函数是熵正则下的值函数, 即定义(4),此时最优策略是唯一的,且具有显示的表达式。如果我们定义奖励函数 下的的最优策略为, 对应的每个状态和状态动作对处的最优值函数分别为,, 那么根据 Bellman optimality equations 中与
即,如果我们知道了每个奖励函数 下的最优熵正则Q函数, 我们就能得到RL后的最优值函数。作者最聪明的一点在于,巧妙观察了Bellman equations 中 奖励函数与Q函数中的关系,将问题化简。 给定任意一个奖励函数与策略, 根据Bellman equation, 我们有策略 的Q函数 满足 :
同样的给定任意一个奖励函数 , 最优策略 的Q函数 满足 :
观察 (9)与(10) 我们可以知道 : 知道 后求解Q函数很难,但是如果反知了Q函数,求解 很容易。作者文中的推导都是基于(9)进行,这里我们基于(10)进行。 根据 (10), 我们可以得到:
也就是说,如果我知道了 ,我可以很轻易的知道,对应的奖励函数 是什么。因此我们可以定义inverse Bellman operator , 给定任意向量 , 我们定义
根据定义可以知道,如果我们认为 Q 是某个奖励函数下的熵正则最优值函数,那么 实际上就是找到使其满足最优性的对应的奖励函数。也就是说如果我们以 作为奖励函数求解最大熵RL,那么对应的最优值函数实际上就是 Q。即奖励函数与Q函数的tuple, , 满足Bellman optimality equation. 于是给定任意奖励函数 , 对应求解后的最优值函数为 ,由于 满足Bellman optimality equation, 那么必然有:
因此 inverse Bellman operator 建立了一个从Q vector space 到 reward vector space的映射,如图
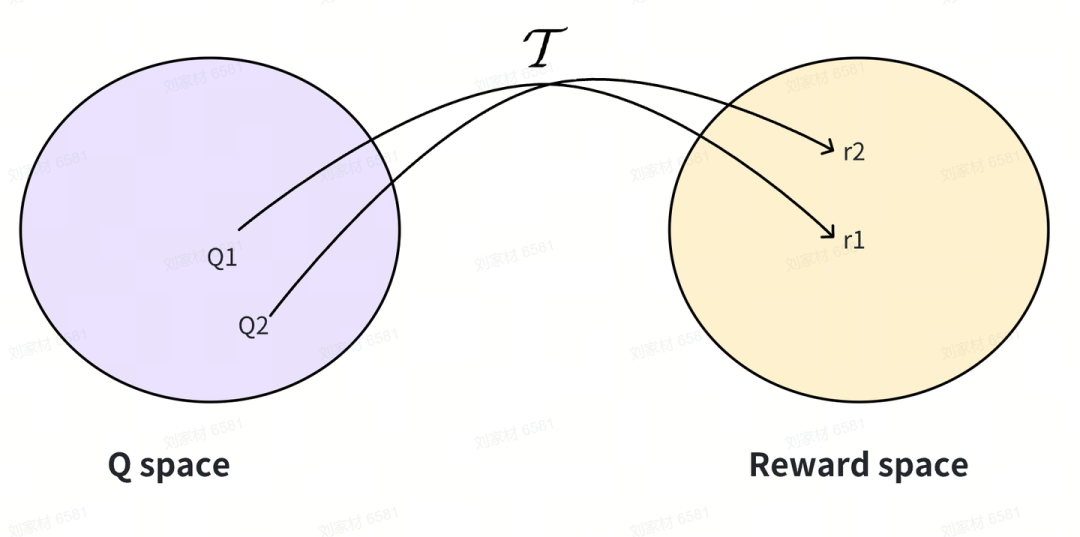
作者在[6]中证明了 inverse Bellman operator 在离散状态动作空间下是一个从reward space 到 Q space 的一个一一映射。 从而我们可以将 正则IRL目标(5) 中 对 reward space 求max 的操作, 转换成对Q space 求max 的操作,同时利用 的一一映射属性, 替换边际函数内的 :即
注意到我们对 的定义(11),给定任意一个 Q ,以 作为奖励函数的最优Q值函数就是Q本身,从而根据(8)
如果我们继续考虑正则项满足
其中 是一个convex 函数 (从而 也是), 那么我们正则IRL目标可以继续写成:
其中
可以看到原始 max-min问题,通过把求解空间从reward space 替换成Q space 与 inverse Bellman operator的介入,巧妙的解决了内层需要求解 的问题,使得整个问题变成了单目标的优化。 具体的算法这里不再过多展开。详情请看论文。
GRM : Generalist Reward Models
最后我们介绍基于IQ-Learn中 inverse Bellman Operator 思想的南大的工作 《Generalist Reward Models: Found Inside Large Language Models[1]》 。根据我们在上一节中对inverse Bellman operator的介绍可以知道,任意一个动作状态对上的实值函数Q, 我们都可以通过对其作用来找到一个奖励函数,即, 使得求解上的RL最大熵策略的值函数,就是 Q 本身。 GRM的工作则是充分利用了这一点。注意到我们的LLM token-level的生成实际上是以词表为动作空间,前文token序列的拼接作为状态的MDP。给定任意一个前文状态, next token的生成策略是一个词表 上的softmax 策略, 即:
其中 是transformer参数为 下输出的 logits。注意到 实际上就是一个 上的函数, 那么如果我们根据(11), 定义奖励函数
那么容易知道, 满足最大熵RL的Bellman optimality equation. 从而以为token-level 奖励函数, 跑系数为, 折扣为的最大熵RL 得到的最优Q值函数为. 注意到在LLM token-level MDP中, 环境的转移是确定性的,且我们通常考虑折扣 , 从而奖励可以写为:
其中 表示前文token序列 与生成token 的拼接。于是我们可以从任意logit函数 得到一个内在奖励
诱导内在奖励本质上是模仿奖励
一个核心的问题是,以logit函数 诱导出来的内在奖励,, 在logit函数具有什么属性下是好的? 因为RL的目标是最大化期望累积奖励,因此我们评判奖励函数好不好,可以直接看上对应的轨迹累积奖励,看是否那些具有高奖励的轨迹是我们想要的。考虑最大长度为 T 上的轨迹生成。给定一个轨迹序列其中是是生成的token。为方便起见,我们定义 和
考虑 , 注意到softmax策略满足
于是根据(12)中logit诱导出来的内在奖励 的定义, 任意一轨迹 对应的累积奖励为:
其中, , (a)根据 (13), 最后一行 是因为我们定义RL的决策最大长度为 T ,因此terminal state的value 等于0. 因此,基于上面的推导,如果我们基于内在奖励 作为token-level 奖励,跑无约束RL,那么本质上求解的是:
即希望策略 优化到对应的策略的高概率轨迹上,因此实际上给我们提供了一个模仿策略生成的奖励函数。因此的好坏,本质上依赖于的高概率轨迹的好坏。即如果的高概率轨迹是好的,我们在的上诱导出一个内在奖励上跑RL,可以将我们的actor model对齐到的高概率区域 (模仿),从而产生 的高概率轨迹。
GRM总结
1、任意一个LLM的token 生成策略 , 都可以对logit 函数 作用inverse bellman operator , 诱导出一个内在奖励
使得 满足Bellman optimality equation.
2、给定任意一个LLM生成策略 , 在其诱导出来的内在奖励 上跑无约束RL, 本质上优化的是
会将 actor model 与 的高概率分布对齐。因此 本质上提供了一个模仿 生成的token-level 奖励。
3、结合(1)(2) 所论述,内在奖励 的好坏,依赖于 的生成质量的好坏。因为 的高奖励区域是 的高概率区域。
参考文献
[1]Andrew Y. Ng and Russel Stuart. Algorithms for inverse reinforcement learning. In ICML, volume 1 of 2, page 2, 2000.
[2]Abbeel, P., and Ng, A. Y. 2004. Apprenticeship learning via inverse reinforcement learning. In Proc. ICML, 1–8. https://ai.stanford.edu/~ang/papers/icml04-apprentice.pdf
[3]B. D. Ziebart, A. Maas, J. A. Bagnell, and A. K. Dey. Maximum entropy inverse reinforcement learning. In AAAI, AAAI’08, 2008.
[4]U. Syed, M. Bowling, and R. E. Schapire. Apprenticeship learning using linear programming. In Proceedings of the 25th International Conference on Machine Learning, pages 1032–1039, 2008. https://www.schapire.net/papers/SyedBowlingSchapireICML2008.pdf
[5]B. D. Ziebart, J. A. Bagnell, and A. K. Dey. Modeling interaction via the principle of maximum causal entropy. In ICML, pages 1255–1262, 2010.
[6]Jonathan Ho and S. Ermon. Generative adversarial imitation learning. In NIPS, 2016
[7]Divyansh Garg, Shuvam Chakraborty, Chris Cundy, Jiaming Song, and Stefano Ermon. Iq-learn: Inverse soft-q learning for imitation. In Advances in Neural Information Processing Systems 34, pages 4028–4039, 2021
[8]Yi-Chen Li and Tian Xu and Yang Yu and Xuqin Zhang and Xiong-Hui Chen and Zhongxiang Ling and Ningjing Chao and Lei Yuan and Zhi-Hua Zhou. Generalist Reward Models: Found Inside Large Language Models. Arxiv 2506.23235.
[9]Puterman, M. L. (1994). Markov decision processes: Discrete stochastic dynamic programming. John Wiley and Sons.
(文:机器学习算法与自然语言处理)