LLM 训练终于不用打补丁了!
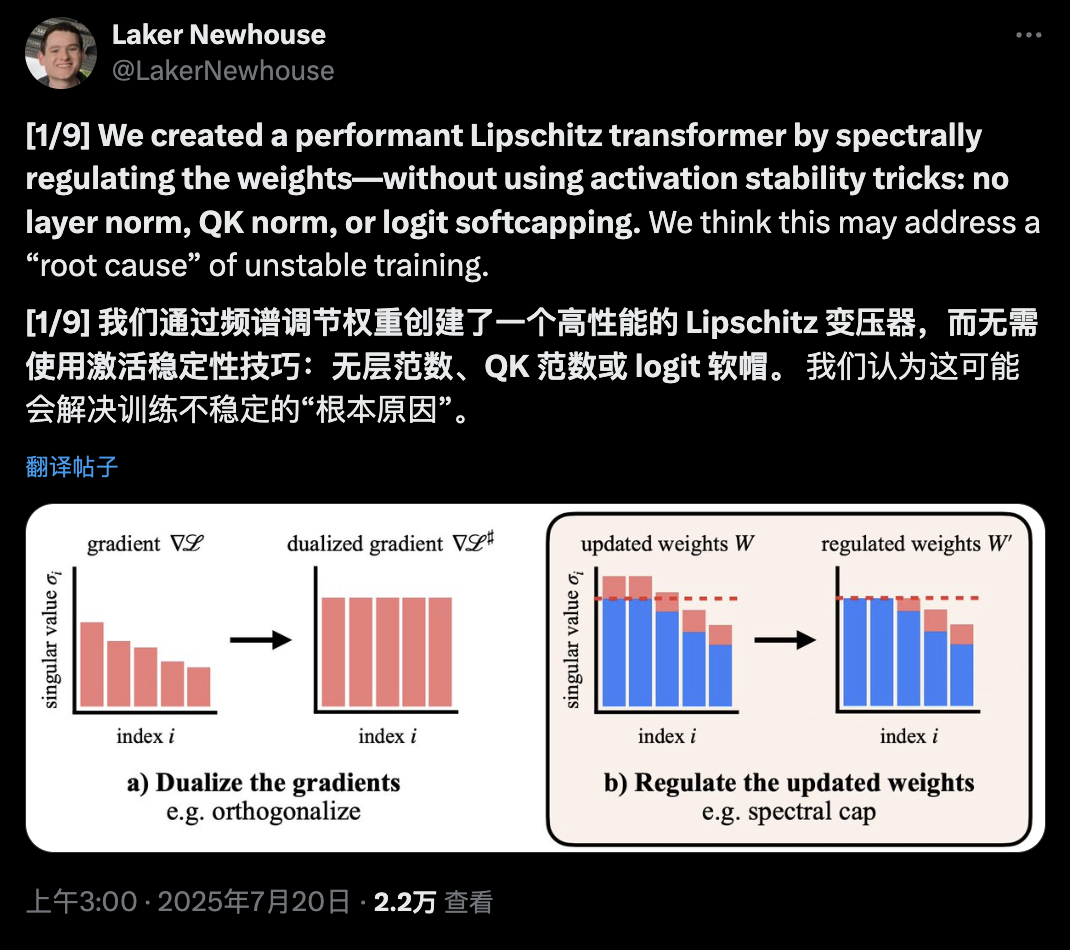
MIT团队创造了一个性能优异的Lipschitz Transformer,通过对权重进行谱正则化——完全不需要激活稳定技巧:没有层归一化、没有QK归一化、没有logit softcapping。
他们认为这可能解决了训练不稳定的「根本原因」。
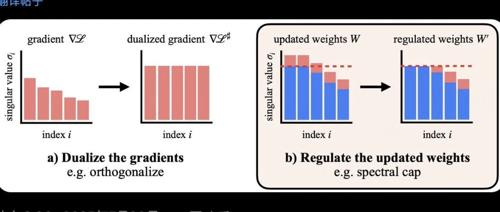
谱正则化:从梯度到权重
Muon原本只对梯度进行谱正则化,但如果我们也对权重进行谱正则化呢?
结果是:激活值保持极小——几乎在fp8范围内。
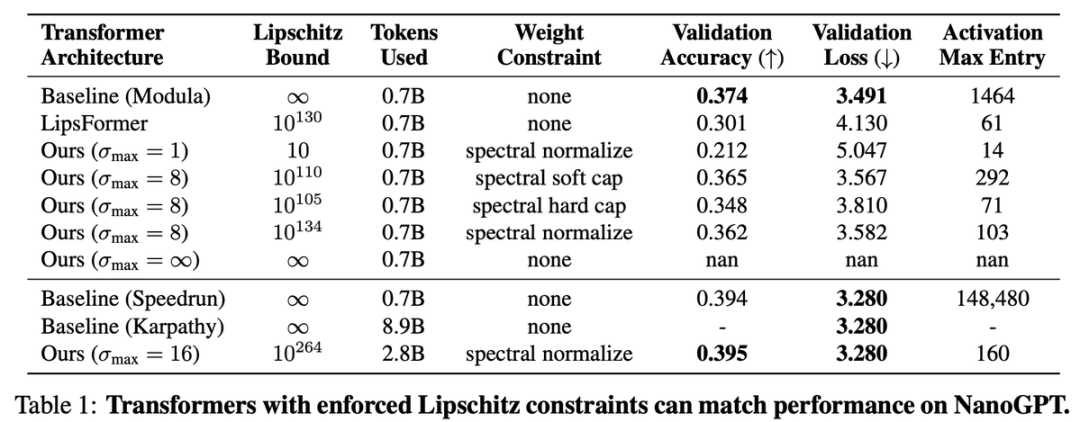
在他们的GPT-2规模Transformer中,激活项不超过约100,而基线模型高达约1000。
论文地址:https://arxiv.org/abs/2507.13338
受Kimi AI启发的高效原语
团队最兴奋的事情之一是受Muon启发并与Kimi AI最近工作相关的高效原语。
他们引入了一系列方法,通过应用min(1, x)来限制奇异值,这是为Muon的高稳定秩更新而协同设计的。
这种设计让奇异值裁剪变得既高效又优雅。
Lipschitz界限的追求
他们的主要目标是在NanoGPT上强制执行可证明的Lipschitz界限,同时匹配无约束的验证损失。
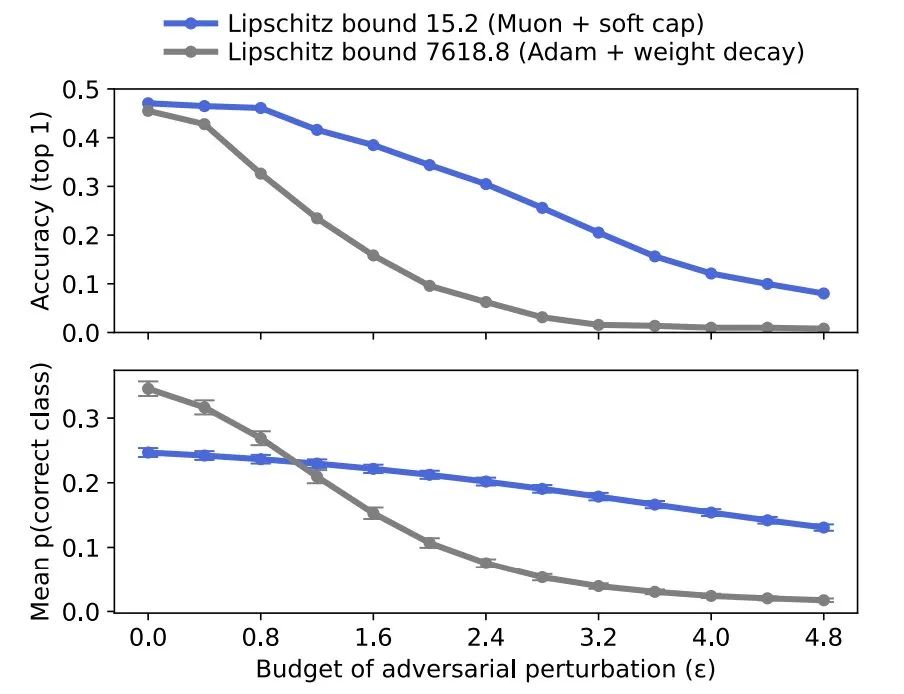
Lipschitz界限控制着网络对输入或权重变化的敏感度。较低的界限意味着:小的输入变化不会导致输出的剧烈变化。
更低的Lipschitz界限 => 更鲁棒、更可预测的模型
但还需要更多工作,目前的方法将Lipschitz常数限制在10^264。
权衡的艺术
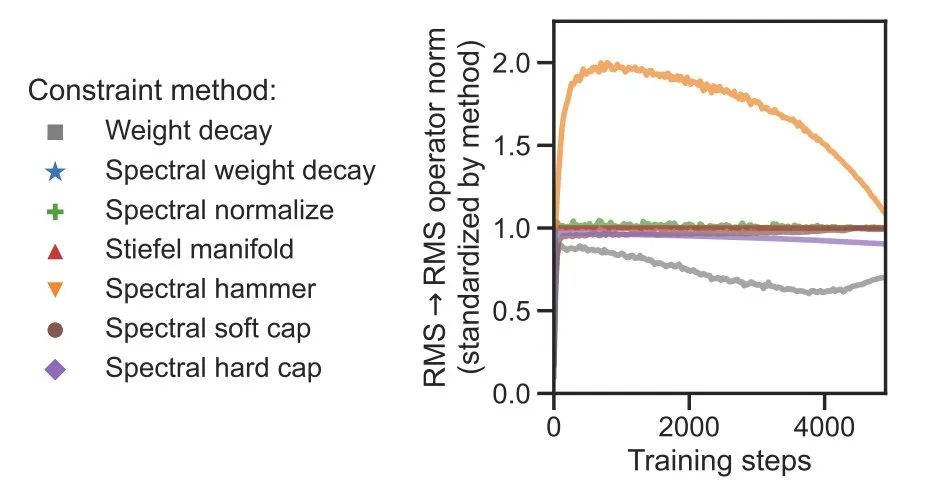
为了控制Lipschitz界限,需要控制权重范数。有很多方法可以做到这一点,包括权重衰减。
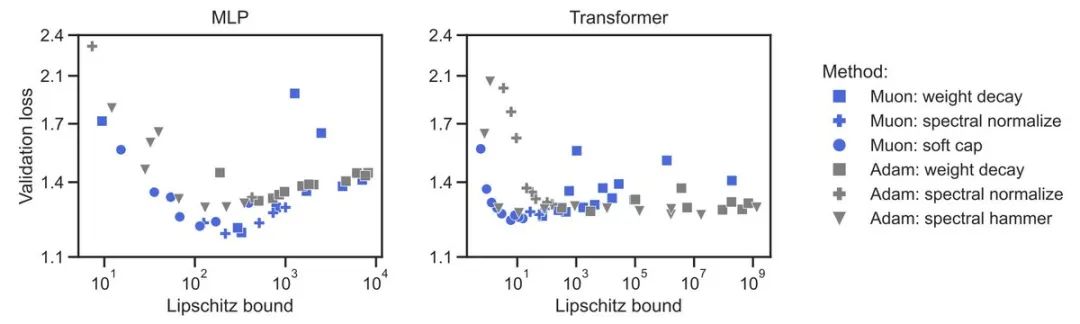
团队比较了各种方法的「Lipschitzness to performance」权衡。
发现:Muon + 奇异值裁剪推动了权衡边界。
社区的智慧碰撞
团队看到了最近涌现的相关工作,包括@Jianlin_S的QK-clip算法和@_arohan_的权重约束线程。
Laker Newhouse(@LakerNewhouse)特别引用了rohan anil(@arohan)的思考:
做一些数学来净化时间线
为什么损失会爆炸?一个值得深思的问题。
所以尝试一下:为什么不裁剪更新的奇异值呢?
σ > 1,裁剪到1 σ <=1,返回σ
朴素实现:
Update = U S V.T Update_clipped = U clip(S, 1) V.T
如何让它更快?有迭代算法吗?欢迎社区贡献
一个可能的实现:
在[0, σ_max]之间创建一个非常高阶的切比雪夫多项式
在[0, 1]之间保持接近[1-eps, 1+eps]
在[1, σ_max]之间让它快速衰减
让我们称之为Sion,赶上潮流。
现在让我们看看能否做得更好
给数值线性代数专家的开放问题
有更快的算法将最大值裁剪到1.0吗?朴素实现是幂迭代和缩减 给我的优化专家们
我们应该相对于权重矩阵每个分量的变化量进行裁剪吗,更像Wion。 (如果有人之前写过相同的算法,请告诉我参考文献,如果这启发了你做出什么,请引用这条推文)
看到论文后,rohan anil回应说:
我最初还以为你真的引用了那个线程😅
这项工作做得很好!
他还询问:「你认为这条研究路线的下一步是什么?」
cider(@jeffreycider)评论:「很棒的工作!我喜欢『spectral hammer』这个名字」
Emilio(@Em_alej)则在思考更广泛的应用:「太棒了!我想知道这是否可以应用于GANs——将生成器和判别器都使用transformer,有点像ViTGAN。」
完全开源
这项工作是与优秀的朋友和合作者共同完成的:@phess002 @leloykun @anzahorodnii @jxbz @phillip_isola
团队对社区能将这项工作推向何方感到非常兴奋。
他们发布了所有代码和数据,还有很多需要测试和理解的内容,这些可以帮助实现对抗鲁棒性、有界激活和大规模稳定训练。
MIT 的研究又一次呼应了奥卡姆剃刀的思想:
最优雅的解决方案,往往是最简单的。
层归一化、批归一化、各种稳定技巧……这些年来,我们给Transformer加了太多「创可贴」。
而谱正则化的思路是:与其不断修补症状,不如直接治疗病因。
通过控制权重的奇异值,激活值自然就变小了;通过限制Lipschitz界限,模型自然就稳定了。
当我们不再需要各种「稳定技巧」,当模型本身就是稳定的,那才是真正的进步。
虽然10^264的界限看起来还很大,但这已经是一个重要开始。
从Muon到Kimi AI,从MIT到全球的研究者,大家都在思考着相同的问题:如何让AI训练变得更简单、更稳定?
这次,AI 终于有望扔掉所有拐杖,真正学会走路。
论文: https://arxiv.org/abs/2507.13338
[2]代码: https://github.com/Arongil/lipschitz-transformers
[3]数据: https://huggingface.co/phess2/lipschitz-transformers
(文:AGI Hunt)