探索为什么要融合SFT和RL，以及应该怎么融合

作者


MLNLP社区是国内外知名的机器学习与自然语言处理社区，受众覆盖国内外NLP硕博生、高校老师以及企业研究人员。
社区的愿景是促进国内外自然语言处理，机器学习学术界、产业界和广大爱好者之间的交流和进步，特别是初学者同学们的进步。
来源 | 知乎
作者 | 白强伟

 

一、为什么要融合SFT和RL

RL虽然能够有效提升模型的推理能力，但一个重要的前提是基础模型本身具备了一定的相关能力。在RL训练中，通过多次rollout能够采样到正确的轨迹，这样通过RL才能进一步提升。这无疑限制了RL的探索空间。

因此，主流的方式是通过SFT赋予模型一些基础能力，然后在进一步利用RL来提升相关能力。但是一些研究认为两阶段的方式并不是最优的：

  • • [1]通过实验发现，RL能改善中低难度问题的解决能力，SFT则对高难度问题更有效；
  • • [4]则认为更大模型(或者专家)构造的SFT包含跳跃逻辑，通过SFT难以完全模仿这些逻辑，导致进行RL时难以rollout出有效的正样本；
  • • [3]和[5]则直接认为两个独立的阶段本身没有必要存在，应该统一；
  • • [6]进一步分析，发现SFT和RL之间存在着某种对抗，SFT使模型大幅度偏离基础模型，而RL又会将其拉回基础模型；

综上，这些研究均认为有必要将SFT和RL融合为单一阶段。

二、基础知识

在标准的LLM训练流程中，通常包含三个阶段：Pre-training、SFT和RL。Pre-training阶段采用自回归的方式在海量数据上完成预训练，为后续的Post-training奠定基础。Post-training通常分为SFT和RL，这两个阶段均需要一个多样性丰富的prompt集合  。

1. SFT

在该阶段对于prompt  ，会采用专家撰写、人工合成或者强模型蒸馏的方法来构造高质量的响应 y 。这里不妨假设  ，其中  代表人类专家或者更强的模型等。那么，SFT训练的损失函数为

该损失函数的梯度表示为

2. RL

RL通常在SFT阶段后进行。在On-Policy的设定下，对于prompt  ，通常会从当前策略  中采样响应  。RL的损失函数为

该损失函数的策略梯度为

其中，  是针对  的奖励。公式(4)是标准REINFORCE的梯度，在实际中通常为了降低方差会采用带基线的REINFORCE。带基线的REINFORCE本质上是用优势函数来代替奖励，相比于奖励的直接含义，优势函数代表相对于平均状况的改善程度。因此，带基线的REINFORCE的梯度为

其中，  是  的优势。

2.1 GRPO

到目前为止，GRPO已经近乎于LLM后训练中RL算法的事实标准了。GRPO是PPO的一种无critic模型的变种，针对同一个prompt x ，会同时采样 G 个响应  ，每个响应  对应于一个标量奖励  。在标准的PPO中需要critic模型来辅助计算优势，GRPO则采用组内标准化实现优势的近似计算

这里  是指第  个响应的第  个token的优势。除了优势的计算外，损失函数与PPO类似

其中 是重要性采样。

三、交替进行SFT和RL

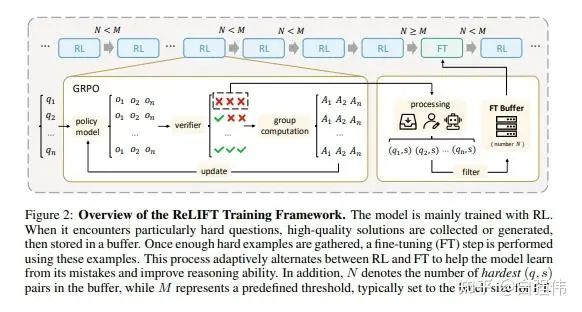
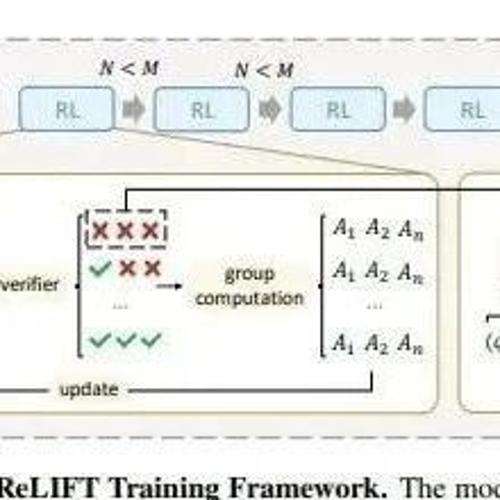
ReLIFT[1]认为RL改善中低难度问题，SFT改善高难度问题。因此，设计了一种交替方案。具体来说，在RL过程中将rollout过程中完全错误的样本放入缓冲池。当缓冲池满时，利用这些样本进行SFT。

四、将SFT用作RL中的Off-Policy样本

相比于交替进行SFT和RL，LUFFY[2]则将SFT用作Off-Policy样本，然后通过重要性采样将其统一在RL过程中。显然，这样的方式更自然一些。

1. 符号

表示直接使用策略进行rollout得到的  条轨迹。

 则是  条SFT数据。

2. 混合On和Off的样本

最简单的方式是直接将Off-Policy的样本混合到On-Policy数据中进行训练，那么损失函数可以写为

其中  是归一化因子。

但是上式中的off policy objective中的重要性采样  如果仍然使用  并不合适，因为分母中的  并不是产生off policy数据  的分布。因此，第一项应该采用新的重要性采样

将新的重要性采样系数(9)替换公式(8)就得到了最终的混合损失函数

3. 重要性采样修正

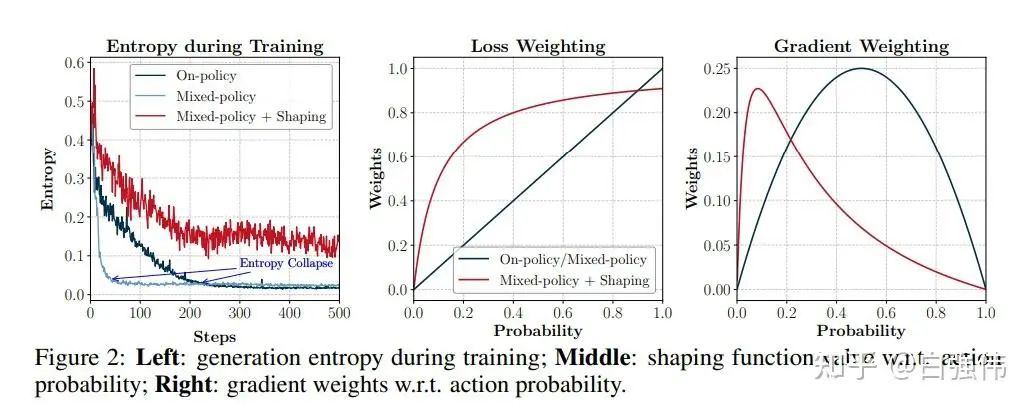
依照公式(10)进行训练，虽然解决了梯度偏差的问题。但是，训练中发现其加速收敛的同时，也显著抑制了探索，导致快速的熵坍缩，如上图左所示。

进一步的分析认为，当模型同时接收On和Off的信号时，其倾向于优先加强那些既存在于On-Policy轨迹中，也存在于Off-Policy轨迹中的概率较高token。那些来自于Off-Policy轨迹中的低概率token，对于推理至关重要，但是由于  太小导致学习信号微弱。

因此，[2]提出利用一个修正函数  来调整重要性采样  ，即使用  替换公式(10)中的  。

 为什么能放大Off-Policy轨迹中的低概率token？

对于Off-Policy部分的损失函数针对  的梯度可以表示为

观察上式可以发现新损失函数相当于在原始策略梯度的基础上添加了一个权重因子 。为了简化分析，可以合理假设离策略对其生成样本的置信度为1，即  。那么权重因子进一步简化为  。

由于  ，当  时，  ，相当于放大梯度。

反之，当 时，  ，这是一个非常小的数，相当于缩小梯度。

五、同时进行SFT和RL

相较于LUFFY[2]通过将SFT视为Off-Policy样本，从而统一至RL。SRFT[6]则进一步采用了偏向于实践的风格，即同时采用SFT和RL损失。

SFT损失函数

标准的SFT损失函数为如公式(1)所示，但是若一个样本的熵太高，则表明该样本对当前模型来说比较陌生。应该降低SFT损失的比例，因此采用带有权重的SFT损失函数

其中

Off-Policy RL损失函数

类似于LUFFY，将SFT视为Off-Policy样本，

其中  同LUFFY的公式(9)。

On-Policy RL损失函数

在二元奖励 {+1, -1}设定下，标准的On-Policy RL损失函数为

但是，SRFT为了缓解熵坍缩，对正样本部分的损失添加了一个基于熵的权重

其中  。当熵较大时，意味着模型对这个样本不太确定，较大的  强制模型更多的学习该样本。

最终的损失函数

将公式(11)、(12)和(13)求和得到最终的损失函数

因此，该方法同时进行SFT、Off-Policy RL和On-Policy RL。

六、将SFT用作hint

hint是指问题和部分正确答案的拼接。标准RL的主要问题是针对难问题无法rollout出正样本。SFT作为天然正样本，可以将其一部分响应与问题进行拼接，从而构造出一个hint。策略基于hint进行rollout，而不是原始的prompt。

基于hint的方法主要围绕两个问题：

  • • a. 如何构造合适的hint？
  • • b. hint部分在训练中怎么处理？

1. 如果构造合适的hint

动态调整hint的长度。[3]和[5]采用了动态调整hint长度的方式，从而构造出难度循序渐进的hint。这种方式即能调整难度，也能缓解训推不一致的问题。假设一条SFT样本的完整长度为 ，[3]使用余弦退火的方式动态调整hint的占比系数。但不直接使用作为hint的长度，而是将视为试验次数，作为成功概率的二项分布，然后基于该分布采样hint长度 。[5]则是从动态区间 U(low,high) 中进行采样，其中上界 high 是固定的，下界 low 则是通过余弦函数从 high 一直衰减到0。这样，模型能够从刚开始基于较多提示才能回答对问题，逐步能够独立回答对问题。

基于rollout的结果调整hint。[4]提出二分搜索的方式寻找合适的hint。具体来说，分如下情况：

  • • 若基于当前的hint进行rollout，所有rollout均失败，则加长hint；
  • • 若基于当前的hint进行rollout，所有rollout均成功，则缩短hint；
  • • 介于二者之间则认为是难度适宜的hint；

2. 训练方式

标准RL训练方式。[4]和[5]均是将基于hint得到的rollout当做普通rollout，采用标准RL进行训练。相比于[4]仅使用基于hint的rollout，[5]则会将标准rollout和基于hint的rollout混合在一起进行训练。此外，[5]认为hint部分直接加入到强化学习中，会强制模型学习概率降低的token，产生巨大梯度，从而导致训练不稳定。因此，需要对来自于SFT部分的token进行筛选，仅保留熵最高的top-k%个token的梯度。

结合SFT和RL训练方式。[3]对于hint部分和rollout部分采用了不同的损失函数。对于hint部分使用SFT损失函数，对于rollout部分使用RL损失函数。具体来说，在GRPO的设定下，每个prompt  会产生  个response  ，每个  的前  部分属于hint。那么，损失函数为

参考文献

[1]. Learning What Reinforcement Learning Can't: Interleaved Online Fine-Tuning for Hardest Questions
链接：https://arxiv.org/pdf/2506.07527
[2]. Learning to Reason under Off-Policy Guidance
链接：https://arxiv.org/pdf/2504.14945
[3]. UFT: Unifying Supervised and Reinforcement Fine-Tuning
链接：https://arxiv.org/pdf/2505.16984
[4]. BREAD: Branched Rollouts from Expert Anchors Bridge SFT & RL for Reasoning
链接：https://arxiv.org/pdf/2506.17211
[5]. Blending Supervised and Reinforcement Fine-Tuning with Prefix Sampling
链接：https://arxiv.org/pdf/2507.01679
[6]. SRFT: A Single-Stage Method with Supervised and Reinforcement Fine-Tuning for Reasoning
链接：https://arxiv.org/pdf/2506.19767

 


（文：机器学习算法与自然语言处理）

发表评论