ICLR 2025 突破深度学习求解PDE的瓶颈，清华提出空间调控新范式GridMix

近年来，深度学习在偏微分方程（PDEs）求解中展现出前所未有的潜力。从气象模拟到材料科学，基于数据驱动的神经网络模型正不断重塑科学计算的边界。尤其是神经场（Implicit Neural Representations，INRs），凭借其连续参数化的特性，能够实现跨几何形态的高分辨率建模，在复杂场景下展现出卓越的精度和灵活性。

然而，当面对具有剧烈空间变化的场景时，现有 INR 方法暴露出明显的瓶颈。传统的全局调控机制要求模型在所有空间位置共享同一组调控参数，这种方式在捕捉局部细节特征时显得力不从心。随着场景复杂度的提升，全局调控不仅限制了模型精度，还导致泛化能力下降。

为了解决这一难题，清华大学研究团队提出了一种创新的空间调控方法 ——GridMix。灵感来源于谱方法的思想，GridMix 将空间调控参数表示为一组网格基函数的线性组合。GridMix 具备以下特点：

• 保留了空间调控的细粒度局部性，确保建模精度；

• 同时通过共享基函数提取全局结构信息，有效缓解了过拟合风险。

在一系列挑战性的 PDE 建模任务中，GridMix 展现出了显著的性能提升。特别是在稀疏空间域和时间外推场景下，其鲁棒性表现尤为突出。该研究已被 ICLR 2025 接收，并获选为 Oral 论文（入选比例 1.8%）。

论文标题：

GridMix: Exploring Spatial Modulation for Neural Fields in PDE Modeling

论文链接：

https://openreview.net/forum?id=Fur0DtynPX

项目主页：

https://github.com/LeapLabTHU/GridMix.git

方法

本文研究聚焦于偏微分方程（PDE）建模任务，其核心是近似算子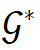。该算子根据底层 PDE，将输入空间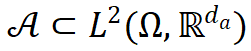中的函数映射到输出空间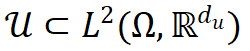。此处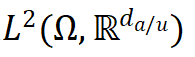表示定义域为且值域为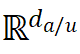的平方可积函数构成的无限维空间。我们重点研究以下两类典型任务：

• 动态系统建模：旨在捕捉物理系统在预测时间范围内的动态演化过程。具体表现为建模系统从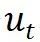状态到状态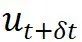的转移过程，其中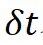表示时间步长。

• 几何感知预测：根据系统的几何构型预测其状态。

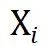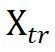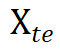在几何预测中，每个数据样本分布于不同的空间域上；而对于动力学建模，所有样本使用相同的训练空间域，测试时则采用与训练域不同的空间域来评估模型性能。需特别说明的是，和均为完整域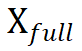的子集。

基于INR的PDE建模方法

CORAL 是最具创新性的 INR 方法之一，它通过两阶段训练策略解决偏微分方程建模问题。

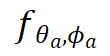在第一阶段（重构阶段），该框架采用两个神经调控场和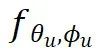分别对输入和输出函数进行参数化建模。这些神经调控场作为基础模型，通过不同调制参数实现对不同函数的重构。

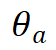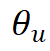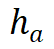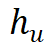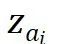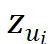具体而言，INR 参数和在各自函数空间中共享，而调制参数和则是每个函数特有的。这些调制参数通过超网络和从低维调控向量和中生成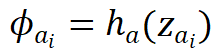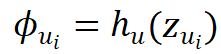：，。经训练后，每个函数可由低维调控向量经过共享 INR 重构，其重构误差代表了表示质量。

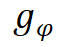在第二阶段（预测阶段），CORAL 通过处理网络学习调控编码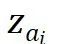与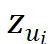之间的映射关系。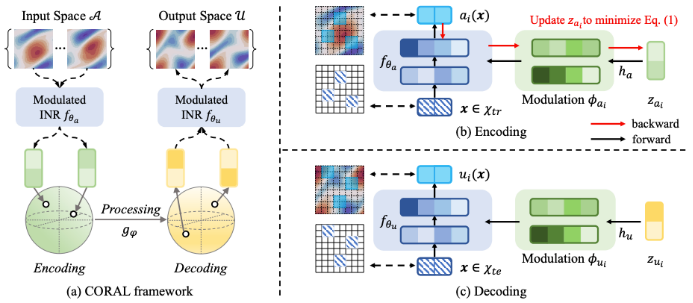

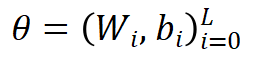▲ 图1. 基于 INR 的 PDE 建模框架

CORAL 的全局调控

CORAL 利用 SIRENs 作为其 INR 的骨干网络。SIRENs 是具有正弦激活函数的多层感知机，可以表示为：

其中，是网络权重和偏置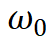，为固定的放缩因子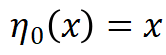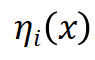，，是空间坐标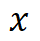下的第层中间表示结果。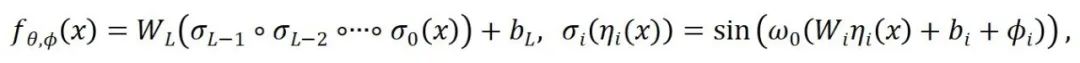

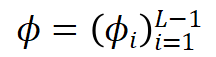CORAL 通过平移调控（Shift Modulation）对 SIRENs 进行扩展，将单个函数表示为：

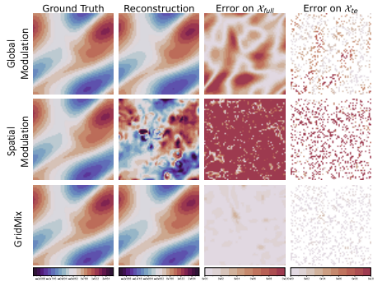
其中表示第 i 层的调制参数。需要注意的是，这种全局调控参数在不同空间坐标之间是共享的。这一特性限制了神经调控场表示复杂函数空间的能力。正如先前的研究所展示的，全局调控无法捕捉局部细节，因为调控参数的任何变化都会导致重构函数的全局扰动。

▲ 图2. 不同调控方式

GridMix

基于网格表征的空间调控方法在提升 INR 学习能力方面展现出显著优势，特别是在三维重建领域，其有效性已被广泛验证。

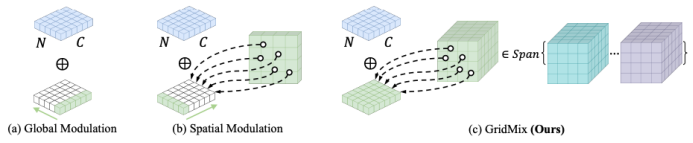
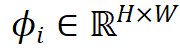受此启发，本文旨在探索空间调控在 PDE 建模中的的应用及其潜在优势。具体而言，空间调控引入了一个基于网格的单通道特征，其中 H 和 W 分别表示网格的空间分辨率（以二维空间为例）。

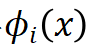我们可以从该网格特征中提取位置相关的调控参数。具体步骤如下：给定空间位置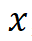，首先提取围绕该位置的相邻网格点（在二维情况下为四个点）上的特征，其次通过双线性插值计算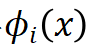。空间调控对应的平移调控方法可表示为：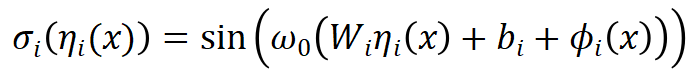

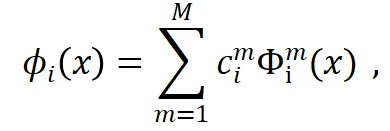
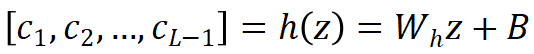空间调控引入的位置相关的调控参数虽擅长捕捉局部信息，却难以在稀疏 / 不规则的空间域中建模全局结构，导致未知区域重建质量骤降（如图 3 所示），从而严重制约跨空间域的泛化能力 —— 而这正是鲁棒 PDE 建模的关键要求

▲ 图3. 重建效果对比：观测数据的空间域在训练集之外

为了缓解空间调控在训练空间域上的过拟合问题，GridMix 将空间调控参数表示为一组网格表征的线性组合，如图 2 (c) 所示。首先，GridMix 定义一组网格表征作为基函数，再通过这些基函数的线性组合生成空间调控参数。具体而言，每一隐藏层的网格混合表示为

其中。这里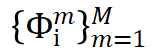表示 M 个网格基函数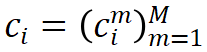，为第 i 层的线性组合系数。这些系数通过超网络 h 从低维调控向量 z 中估计得到。网格基函数在不同的函数实例中共享，并与神经调控场一同优化。GridMix 具有以下特点：

• 局部细节捕捉：GridMix 保留了网格调控的局部特性，通过引入额外的可学习参数增强了模型在局部细节重建的表达能力；

• 全局结构建模：GridMix 通过共享基函数对调控空间起到正则化作用。相比一般空间调控需要为每个函数额外学习个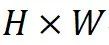独立参数，GridMix 将参数维度降低至基函数的个数。这种维度压缩有效减少了过拟合的风险，提升了模型对全局结构的重建能力，以及在不同空间域上的泛化能力。

实验

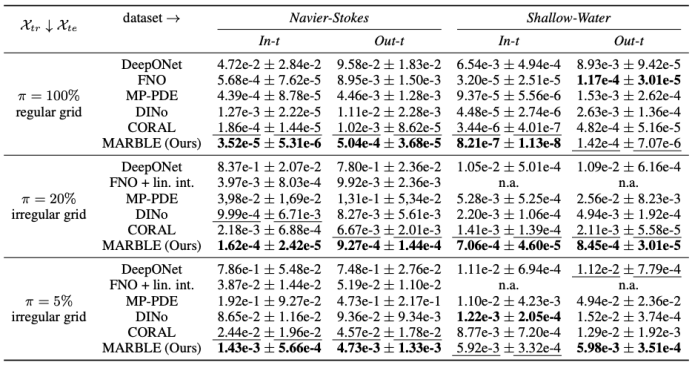
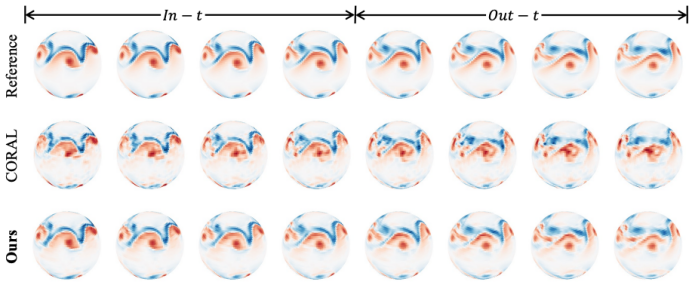
动态系统建模

在 Naviers-Stokes 和 Shallow-Water 两个动态系统建模任务上，GridMix 相比神经算子方法（DeepONet 和 FNO）、图网络方法（MP-PDE）以及基于全局调控的 INR 方法（CORAL）均取得了显著的性能提升。同时，GridMix 在稀疏空间域的重建和时间外推任务中表现出优越的鲁棒性，进一步验证了其广泛的适用性。

▲ 图4. 动态系统建模任务

▲ 图5. 稀疏空间域下的Shallow-Water可视化结果

几何感知推理

在几何感知推理中，模型根据给定的几何结构（例如翼型（NACA-Euler）、水管（Pipe）和弹性材料（Elasticity））预测系统的状态。相较于全局调控方法，GridMix 在所有任务中均实现了性能提升。

▲ 图6. 几何感知推理任务

总结

本文的贡献主要在两个方面：

• 提出了一种新颖的空间调控方式 ——GridMix，它自然地融合了全局调控的全局结构建模和空间调控的局部细节捕捉能力；

• 在动态系统建模和几何感知推理等任务中充分验证了 GridMix 的卓越性能，特别是在稀疏空间域和时间外推场景下优势显著。

（文：PaperWeekly）