赶在五一假期前夕，DeepSeek 给我们送出一份惊喜大礼。
延续一贯的开源节奏，DeepSeek 在 Hugging Face 正式发布 DeepSeek-Prover-V2，并同步上线模型卡及示例代码。此次共推出两个版本：
DeepSeek-Prover-V2-7B：基于上一代 V1.5 模型，支持最长 32K 上下文输入；
DeepSeek-Prover-V2-671B：在 DeepSeek-V3-Base 基础上训练，推理性能最强。
*核心贡献者 †在 DeepSeek-AI 实习期间完成的工作，扫描文末二维码，进社群获取完整报告
据官方论文披露，DeepSeek-Prover-V2 的训练核心是「递归+强化学习」的组合：即先由 DeepSeek-V3 拆解复杂定理，生成一系列子目标和推理思路；再通过 GRPO 算法，从多种候选方案中自动学习如何选出最优解。
模型特别引入了两种互补的「解题风格」：
快速模式（non-CoT）：专注于速度，像是一位熟练工匠，直接生成精炼的 Lean 代码答案，不展示思考过程，适合处理大量题目。
逻辑模式（CoT）：更像一个耐心的数学老师，会详细列出每一步推理过程，确保逻辑清晰、思路透明。
训练过程分为两阶段，在第一阶段，研究人员主要训练快速模式，采用「专家迭代」方法：模型先尝试解决难题，成功的答案再作为新数据反哺模型，不断打磨自己的能力。
待快速模式趋于稳定后，研究人员进入第二阶段，开始训练更复杂的逻辑推理能力。他们将 DeepSeek-V3 的数学知识迁移到新模型中，并结合形式化数据，引入「冷启动」机制，构建起更复杂的推理路径。
为了进一步提升推理能力，研究人员引入了 GRPO 的强化学习算法，不同于传统的 PPO，它直接在多个候选答案中比较优劣，引导模型自主学会选择最优解。
具体做法是：每次输入一个定理，系统会生成 32 个不同的证明方案，然后只保留被 Lean 验证系统判定为「正确」的答案（奖励 1 分，否则 0 分），这样模型就能在高质量反馈中不断进化。
在开发出性能强大的 671B 模型后，DeepSeek 研究团队又尝试把这些能力「蒸馏」到更小的 7B 模型中，而整个过程就像是师傅教徒弟:
先用大模型生成解题过程，再教会小模型理解并复现；同时将小模型输入长度扩展至与大模型一致，并经历相同的强化训练。
这样，即便在资源有限的设备上，用户也能使用小体积模型获得接近大模型的数学推理能力，并根据需求选择快速或详细解题风格。
整个体系中，DeepSeek-V3 负责拆解复杂定理，生成自然语言的推理草图，同步转译为 Lean 语言表示的一系列子目标，并生成「思路链」作为中间引导。
7B 模型再一步步完成子证明，最终拼接成完整推理。这种「模糊思考 + 精确证明」的训练机制，有效提升了小模型的数学理解深度。
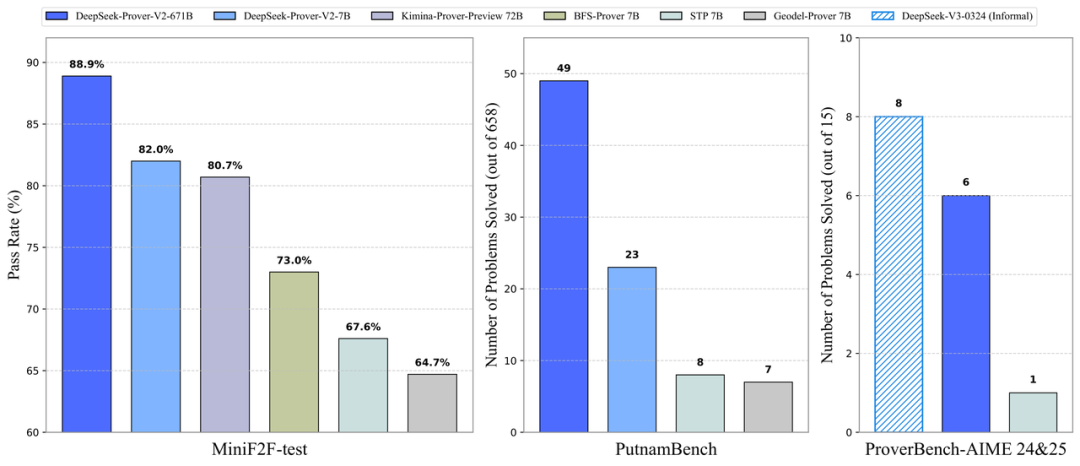
在最终性能评估中，DeepSeek-Prover-V2-671B 在 MiniF2F 测试中实现了 88.9% 的通过率，成功解出 PutnamBench 数据集中的 49 道难题。
与此同时，DeepSeek 还同步推出了一个全新的数学形式化数据集 ProverBench，共包含 325 道问题题目。涵盖：
这一数据集不仅包含真实的高中竞赛题目，还涵盖从基础代数、实变分析到概率论等多个本科阶段知识点，能够系统评估模型在不同数学领域的推理能力。
结果显示，在 15 道 AIME 竞赛题中，DeepSeek-Prover-V2 成功解出其中 6 道，而 DeepSeek-V3 使用多数投票方式（majority voting）则解决了 8 道。
按照官方的说法，这组对比凸显出一个重要趋势：大型语言模型在「非正式数学推理」和「正式数学推理」之间的表现差距正在明显缩小。
非正式数学推理：指模型像人类一样用自然语言思考、理解并解答数学题，比如我们日常说「这道题怎么算？」的方式。它更灵活、不需要严格的逻辑形式。
正式数学推理：指模型能用像 Lean 这样的形式语言，写出符合数学逻辑、可被验证器检验的严谨证明。它像数学论文中的证明，强调每一步推理都必须严格准确。
换句话说，过去模型更像是「会算但不会写出严谨证明」。而现在，在模型结构和训练策略不断演进下，语言模型也逐步学会了写出规范、可验证的数学证明。
此外，DeepSeek 宣布新模型的使用将遵循其公开许可证。
🔗 https://github.com/deepseek-ai/DeepSeek-Prover-V2/blob/main/LICENSE-MODEL
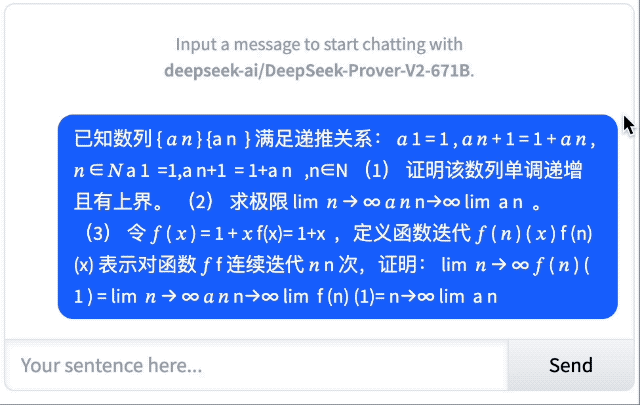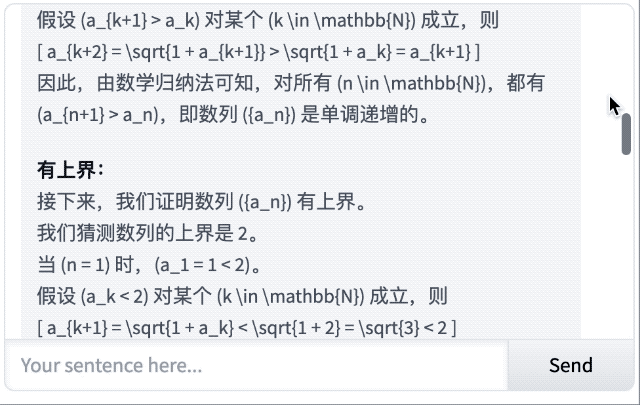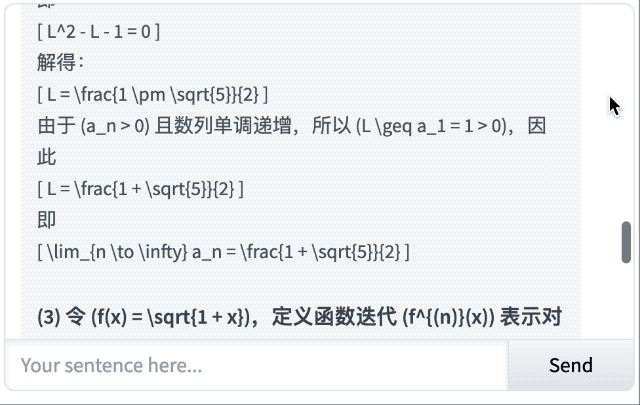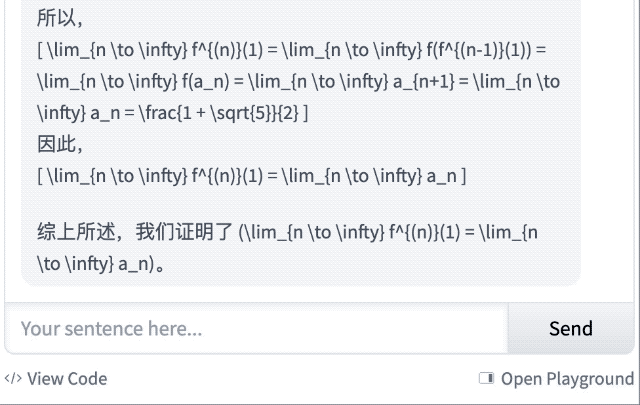
目前，Prover-V2 系列已可通过 Hugging Face 平台免费下载，并支持 Transformers 接口部署。Novita AI 是首批上线 Prover-V2-671B 推理服务的第三方提供商，我们也借此测试了一些问题。
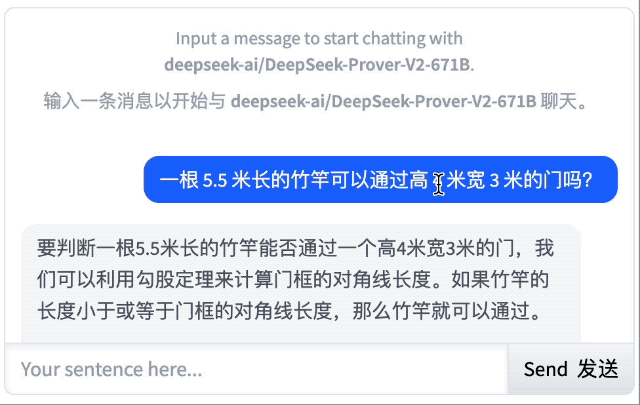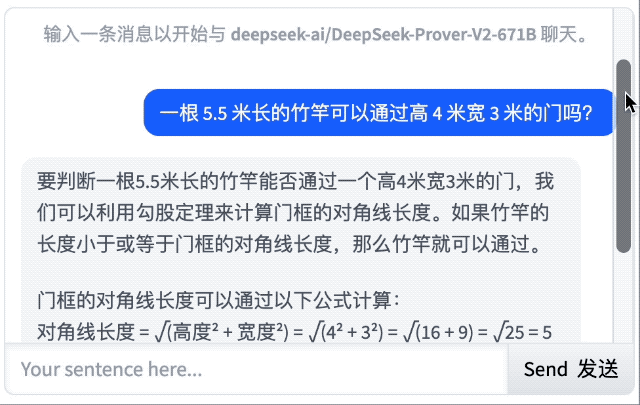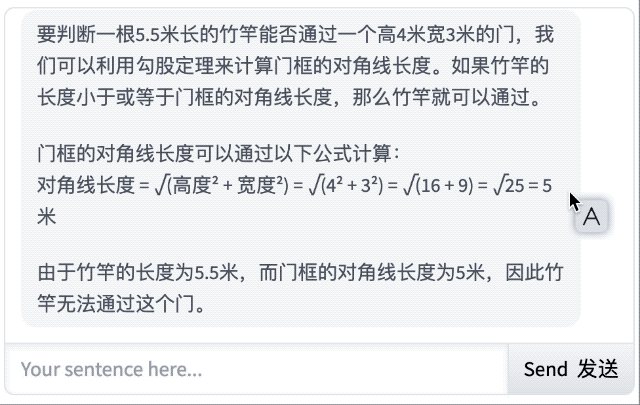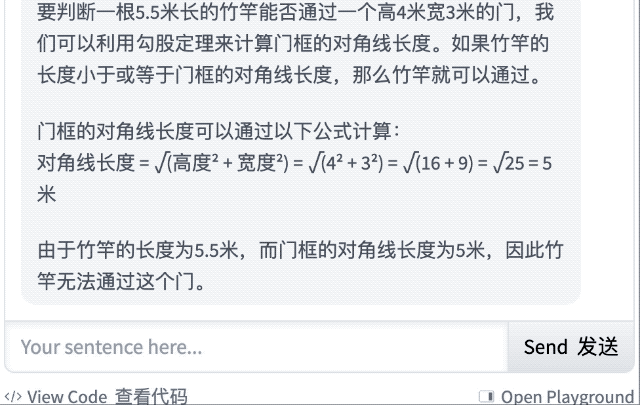
经典的「一根 5.5 米长的竹竿可以通过高 4 米宽 3 米的门吗？」很遗憾，结果它没答对。
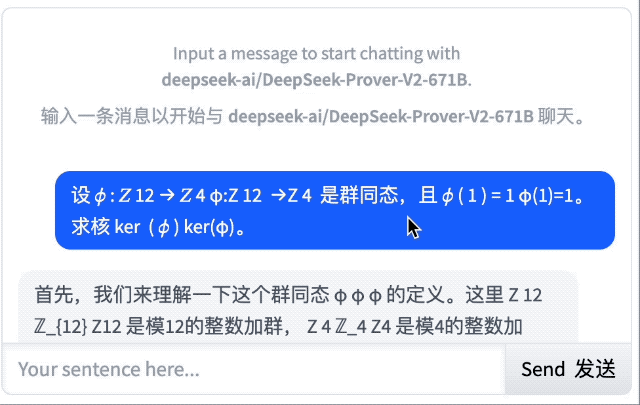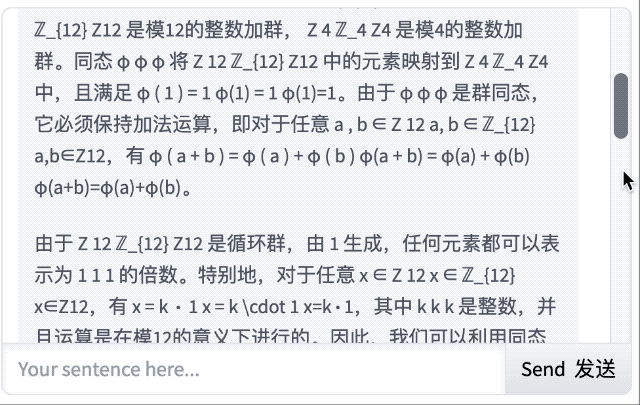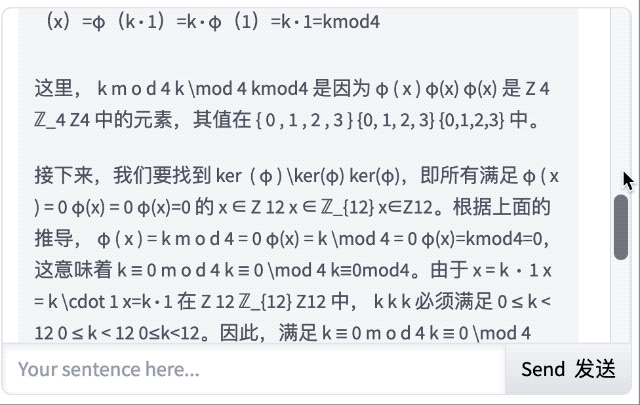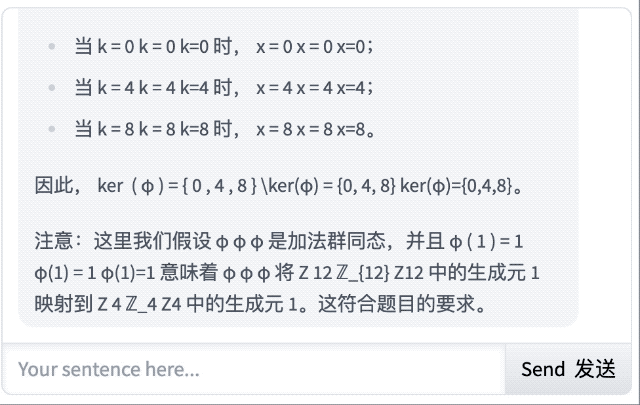
对于这道抽象代数，它的回答不仅正确，还能从基本定义出发，解释了什么是群同态、Z₁₂ 和 Z₄ 的含义，以及同态的运算规则，显然，这对于初学者很友好。
从论文所透露的方向来看，DeepSeek-Prover-V2 给出的不仅是数学答案，更指明了语言模型下一阶段的可能路径。
如果说过去我们关心的是大模型「能说什么」，那么在 Prover-V2 身上，我们得需要关注它「能证明什么」。
数学只是切入口，推理才是 DeepSeek 这次真正下注的方向。
从生成内容迈向生成结构化逻辑，这条路线不够性感，也不容易讲故事，却可能最早触碰通用人工智能的底层结构。
毕竟，AI 可以不懂人情世故，但它必须学会推理，因为任何知识系统的边界，归根结底都是逻辑能否闭环、以及推理能否成立。
1️⃣ DeepSeek-Prover-V2-7B HuggingFace 地址：
https://huggingface.co/deepseek-ai/DeepSeek-Prover-V2-7B
2️⃣ DeepSeek-Prover-V2-671B HuggingFace 地址：
https://huggingface.co/deepseek-ai/DeepSeek-Prover-V2-671B
3️⃣ DeepSeek-ProverBench HuggingFace 地址：
https://huggingface.co/datasets/deepseek-ai/DeepSeek-ProverBench
4️⃣ DeepSeek-Prover-V2 GitHub 地址：
https://github.com/deepseek-ai/DeepSeek-Prover-V2
