作者介绍:本文第一作者是丰田工业大学芝加哥 PhD 学生杨晨晓,研究兴趣是机器学习理论和大模型推理,在 ICML,NeurIPS,ICLR 等顶级会议上发表过论文。
本文提出一个交替「推理 – 擦除」的深度思考新范式 PENCIL,比传统 CoT 更高效地解决更复杂的推理任务。理论上,我们证明 PENCIL 可用最优空间与最优时间下解决所有可计算问题,而这对于传统的 CoT 是不可能的!该工作已被机器学习顶会 ICML 2025 收录。

-
题目: PENCIL: Long Thoughts with Short Memory
-
链接: https://arxiv.org/pdf/2503.14337
-
代码: https://github.com/chr26195/PENCIL
最近的大模型(如 OpenAI 的 o1/o3、DeepSeek 的 R1)发现能通过在测试阶段深度思考(Test-Time Scaling)来大幅提高模型的推理能力。目前实现深度思考的关键在于使用长链思维链(Long Chain-of-Thought,CoT),即让模型生成更长中间结果得到最终答案。然而,传统「只写不擦」的方法在处理高难度、大规模任务时面临以下瓶颈:
-
超出上下文窗口:一旦链条过长,就会触及模型的最大上下文长度限制;
-
信息检索困难:随着上下文不断累积,模型难以从冗长历史中 Retrieve 关键线索;
-
生成效率下降:上下文越长,每步生成新 token 的计算量越大。
不过实际上,并非所有中间思路都后续推理有用:例如定理证明里,引理一旦验证通过,其具体推导可被丢弃;解数学题时,已知某条思路走不通就无需保留那段「尝试」的细节。纵观计算机科学的发展历史,这一「随时清理」的理念早已渗透到几乎所有计算模型之中:从最早的图灵机模型中,已读写的磁带符号可以被覆盖或重写,直到现在高级编程语言中,垃圾回收机制会自动清理不再可达的内存单元。
基于这样的动机,我们提出一个新的深度思考范式 PENCIL,迭代地执行生成(Generation)和擦除(Reduction),即在生成的过程中动态地擦除不再需要的中间结果,直到得到最后的答案。
一、交替「生成 – 擦除」的深度思考范式
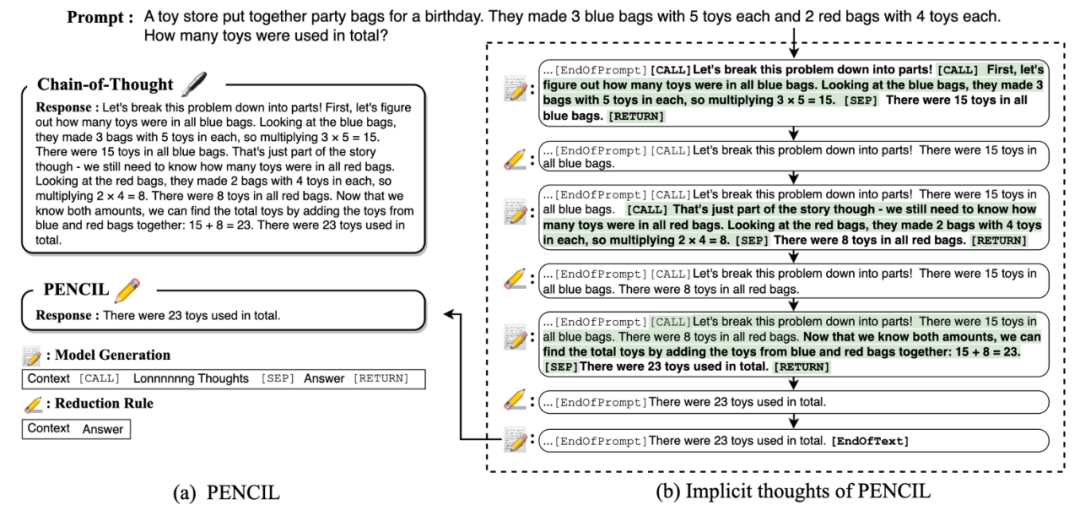
下图以一个简单的算术题为例展示了 PENCIL 的工作机制:
-
CoT 将每步推理串联到上下文中直到给出答案并返回整个序列。
-
PENCIL 交替执行生成(图中加粗部分)和 擦除(图中绿色高亮部分):模型先写出新的思考过程,再删掉对之后的推理无用片段,只保留对后续的推理过程有用的部分,内部形成一系列隐式思维,最后仅返回最终答案。
PENCIL 擦除机制的设计借鉴了逻辑学与经典自动定理证明中的重写规则(Rewriting Rule 和函数式编程语言中的栈帧内存管理(Stack Frame)。 具体地,我们引入三个特殊字符(Special Token),叫做 [CALL], [SEP], [RETURN],并用以下的规则(Reduction Rule)来实现擦除:
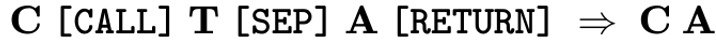
其中 C(Context)表示上下文,T(Thoughts)表示中间思考,A(Answer)表示回答。每当生成的序列与左侧模式完全匹配时,PENCIL 即触发一次擦除,丢弃 T。重要的是,C、T、A 本身均可包含其他特殊标记,从而支持类似多层函数调用的递归结构。
PENCIL 的擦除机制能够灵活支撑多种推理模式,例如:
-
任务分解(Decomposition):通过 [CALL] 启动子任务,完成后用 [RETURN] 合并输出并擦除子任务推理细节;
-
搜索与回溯(Search and Backtrack):在搜索树中,用特殊字符管理探索分支,冲突或失败时擦除无效路径;
-
摘要与总结(Summarization):将冗长的思考片段归纳为简洁摘要,类似编程中的尾递归(Tail Recursion):

其中 T 表示原始的复杂思考过程(或更难的问题),T’ 归纳或简化后的摘要(或等价的、更易处理的问题)。
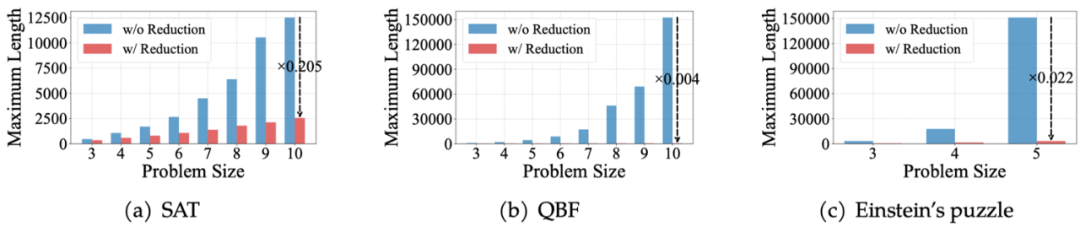
示例: 布尔可满足性(SAT)是经典的 NP-Complete 问题:给定一个 n 个变量布尔公式,判断是否存在一组变量赋值使其为真。这个问题(广泛认为)需要指数时间但仅需多项式空间来解决,其中最简单的做法是构造一个深度为 n 的二叉搜索树遍历所有可能。传统 CoT 将每步计算附加到上下文,长度与搜索树节点数成正比 (O (exp (n))),导致指数爆炸;PENCIL 在递归分支尝试时,遇到冲突立即回溯并擦除该分支所有思考,仅保留关键结果,使上下文长度仅与搜索深度成正比 (O (n))。
如图所示,对比 CoT 无擦除(蓝)与 PENCIL 擦除(红)两种思考模式下的最大上下文长度,随着问题规模增大,PENCIL 能将所需序列长度控制在千级或百级,而传统 CoT 则迅速攀升至数万甚至数十万。即使在复杂的 Einstein’s Puzzle 中,PENCIL 也能将需要几十万 token 的上下文压缩到几千 token。
二、训练和实验结果
训练和测试:在训练时,CoT 每个新 token 的损失计算都基于完整的历史上下文;PENCIL 在每轮「写 — 擦」循环结束后只在被擦除后的短序列上计算损失。即使两者生成 token 数量相同,PENCIL 每一个 token 对应的上下文长度却大幅缩短;另一方面,在每次 Reduction 后,C 部分的 KV cache 可以直接复用,只需为更短的 A 部分重新计算缓存。这样, PENCIL 在训练和测试时能显著减少自注意力计算开销。
实验设置:我们针对三种具有代表性的高难度推理任务构建数据集:3-SAT(NP-Complete)、QBF(PSPACE-Complete)和 Einstein’s Puzzle(自然语言推理)。所有实验均在相同配置下从随机初始化开始进行预训练和评估,采用小型 Transformer(10.6M 参数和 25.2M 参数),训练超参数保持一致。
1. 准确率
相比 CoT,PENCIL 能解决更大规模的推理问题。如下图所示,在 SAT(左图)和 QBF(右图)任务中,当问题规模较小时,CoT 与 PENCIL 均能完美解决问题;但随着规模增大,传统 CoT 的准确率显著下降(例如 SAT 在 n=10 时仅约 50%),而 PENCIL 始终保持 ≥ 99% 的高准确率。
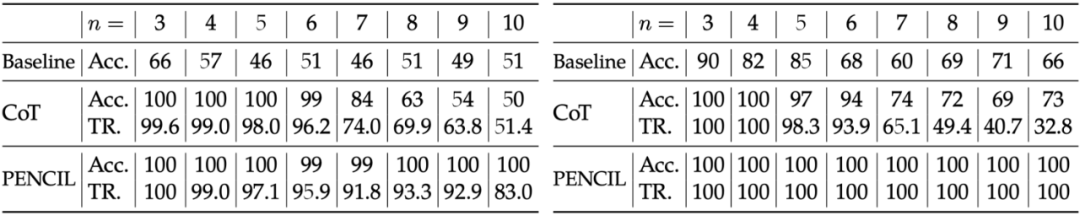
2. 计算效率
PENCIL 还能显著节省计算资源。如图所示,我们在相同 FLOPs 预算下对比了 CoT(蓝色)与 PENCIL(红色)的训练收敛表现。PENCIL 训练早期迅速达到 100% 准确率,训练损失更快稳定;CoT 因上下文膨胀需投入更多资源才能接近最优。随着问题规模增加,两者之间的差距愈发明显。
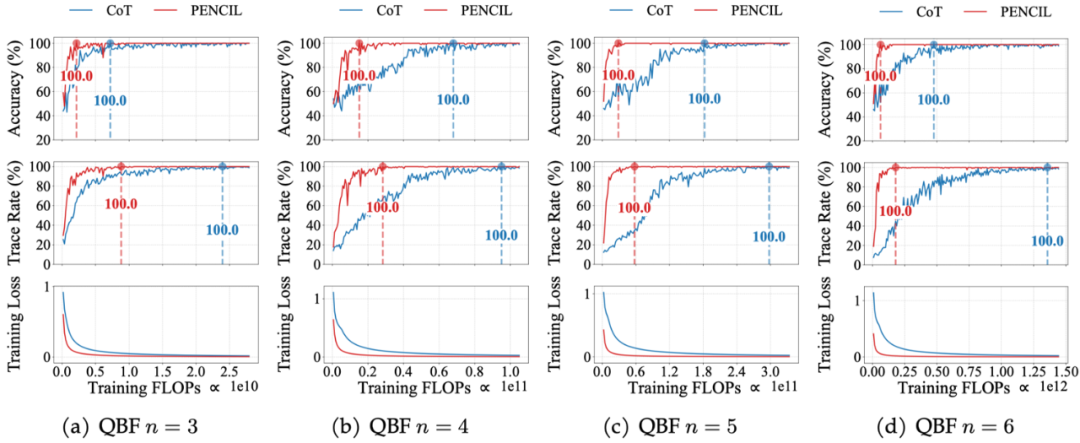
3. 自然语言推理任务:Einstein’s Puzzle
我们测试了 PENCIL 在极具挑战性的 Einstein’s Puzzle 上的表现。该问题要求从一系列线索(如「绿房子在养鸟者右侧」、「养狗者住在红房子」等)推断出五个房屋中人们的全部属性(颜色、国籍、饮品、香烟和宠物)。即使是 GPT-4 也难以解决此类逻辑推理问题 [1]。下图展示了 n=3 时的问题简化:
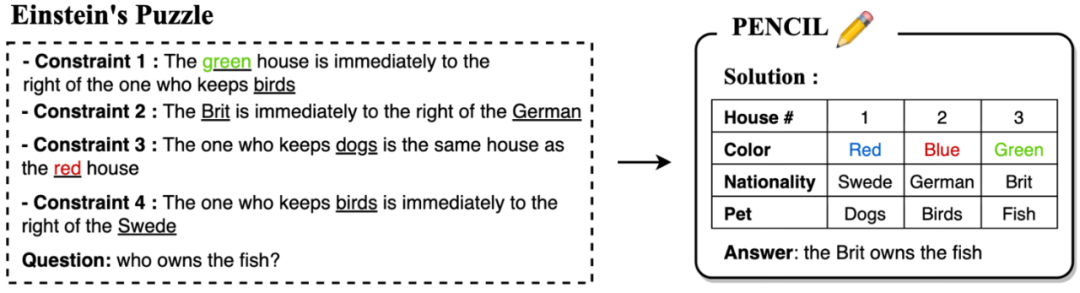
如图所示,对于该大模型也难以解决的问题,而 PENCIL 仅用一个 25.2M 参数的小模型将准确率提升至 97%;相比较之下,传统 CoT 准确率仅 25%,接近随机猜测的准确率。
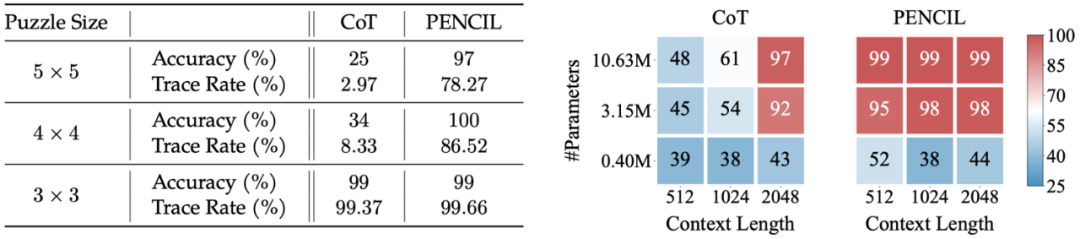
三、理论:PENCIL 用最优的空间 / 时间实现图灵完备
我们进一步从理论表达能力的角度展示 PENCIL 相较于传统 CoT 的根本性优势。具体地,我们证明:使用一个固定的、有限大小的 Transformer,PENCIL 可以用最优的时间和空间复杂度模拟任意图灵机的运算过程(即实现图灵完备),从而高效地解决所有可计算问题:

具体而言,若任意图灵机在某输入上需 T 步计算和 S 空间,PENCIL 仅需生成 O (T) 个 token 并保持上下文长度至多为 O (S) 即可输出相同结果。值得注意的是,大多数算法的空间复杂度都远小于其时间复杂度,即 S << T。
相比之下,传统 CoT 虽能实现图灵完备 [2] —— 思维链的每一步表示图灵机的一步中间计算过程,因此思维链足够长就可以解决所以可计算问题。但这意味着其生成序列的上下文长度必须与运行步数 T 成正比,代价十分昂贵:对于中等难度任务也许尚可承受,一旦面对真正复杂需要深度思考的问题,这种指数级的上下文爆炸就变得不切实际。
例如,一系列(公认)无法在多项式时间内解决却可在多项式空间内解决的 NP-Complete(如旅行商等等),对于使用有限精度 Transformer 的 CoT 而言至少需要超越多项式(例如 exp (n))规模的上下文长度,在真实应用中由于内存的限制完全不可行;而 PENCIL 只需 poly (n) 规模的上下文就能高效求解,让「深度思考」变得切实可行。
证明思路:证明关键在用一系列「思考 — 总结」循环来替代持续累积的思维链。
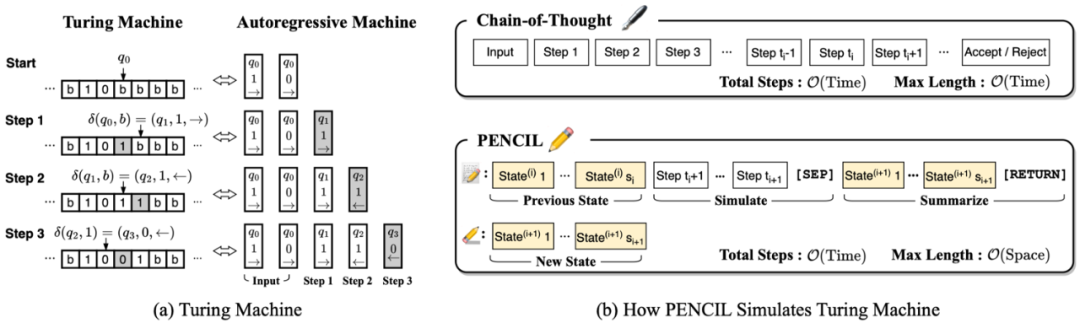
具体地,如上图左图所示,我们先将图灵机状态转移编码为三元组 token(新状态、写入符号、移动方向)。模型通过自注意力计算读写头位置,并从上下文回溯读取符号。未经优化时,需保留 T 步完整历史,上下文长度为 O (T)。
PENCIL 能够实现空间 / 时间最优的核心是利用交替「思考 – 总结」的生成方式:
-
思考 (Simulation):生成连续状态转移 token,模拟图灵机计算;
-
总结 (Summarization):当新 token 数超过实际所需空间两倍时,用不超过 S 个的 token 总结当前状态,触发擦除规则丢弃中间过程。
通过这种策略,PENCIL 生成总 token 数仍为 O (T),却把最大上下文长度严格限制在 O (S),达到了空间与时间的双重最优。
最后,我们需要证明这种「思考 – 总结」的生成方式可以被现实中的 Transformer 实现。为此,我们设计了 Full-Access Sequence Processing (FASP) 编程语言,并证明所有用 FASP 写的程序都可被 Transformer 表达。通过构造能执行「思考 – 总结」操作的 FASP 程序,我们证明了等价存在固定大小 Transformer 完成相同功能,从而理论上证明 PENCIL 可用最优复杂度模拟任意计算过程。
参考文献
[1] Dziri, Nouha, et al. “Faith and fate: Limits of transformers on compositionality.” in NeurIPS 2023.
[2] Merrill, William, and Ashish Sabharwal. “The expressive power of transformers with chain of thought.” in ICLR 2024.

©
(文:机器之心)